| [1969] Alma | 2007-04-12 18:14:51 |
 Nekem is valami hasonló jött ki, csak én megkaptam a végtelen sok megoldást. Nem kell sokat változtatni az előző megoldáson, csak egy icipicit: a) 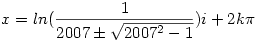 A b) eseten még nem gondolkoztam. A b) eseten még nem gondolkoztam.
|
| Előzmény: [1968] Lóczi Lajos, 2007-04-12 13:53:55 |
|
|
|
|
| [1965] Lóczi Lajos | 2007-04-11 22:22:31 |
 313. feladat. Adjuk meg az összes olyan x (komplex) számot, amelyre
a.) cos (x)=2007
b.) 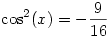 . .
|
|
|
| [1963] Cckek | 2007-04-09 10:40:38 |
 Kellemes ünnepeket mindenkinek.
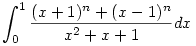 mely n-re racionális? mely n-re racionális?
|
|
| [1962] Cckek | 2007-04-06 07:35:31 |
 Ha már algebrai strukturáknál tartunk... Legyen A egy 4 elemű gyűrű. A akkor és csak akkor test ha az x2+x+1=0 egyenletnek van egy gyöke A-ban.
|
|
|
| [1960] Lóczi Lajos | 2007-04-02 01:28:13 |
 (Még néhány ilyen típusú, érdekes feladatot illetően l. pl. Szendrei-Czédli-Szendrei: Absztrakt algebrai feladatok, JATEPress, 1993. Az itteni feladat amúgy a Gyűrűk fejezet 15. feladatában szerepel.)
|
| Előzmény: [1959] nadorp, 2007-04-01 18:31:09 |
|
| [1959] nadorp | 2007-04-01 18:31:09 |
 Először oldjunk meg egy egyszerűbbet, nevezetesen: Ha egy gyűrűben 1-ab invertálható, akkor 1-ba is az. Megoldás:
Feltehető, hogy sem "a" sem "b" nem a zéróelem. Legyen (1-ab)c=1, azaz abc=c-1. Ekkor
babc=bc-b
babca=bca-ba
ba=bca-babca=(1-ba)bca
1-ba=1-(1-ba)bca. Tehát
(1-ba)(1+bca)=1, azaz 1-ba jobb inverze 1+bca. Hasonlóan adódik a bal inverzre is ugyanez az érték.
Mivel (xy)2=x(yxy) és (yx)2=(yxy)x ezért ha 1-(xy)2 inverze c, akor az előzőek szerint 1-(yx)2 inverze 1+yxycx
|
| Előzmény: [1956] Cckek, 2007-03-31 20:27:37 |
|
|
|
| [1956] Cckek | 2007-03-31 20:27:37 |
 Bizonyítsuk be, hogy ha egy gyűrűben az 1-(xy)2 elem invertálható, akkor 1-(yx)2 is invertálható.
|
|
|
|
| [1955] Cckek | 2007-03-29 20:11:02 |
 Hány számjegye van 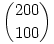 -nak? -nak?
|
|
|
|
|
| [1949] Cckek | 2007-03-27 10:19:18 |
 Bizonyítsuk be, hogy az (R,+) és (C,+) csoportok izomorfak.
|
|
| [1948] Lóczi Lajos | 2007-03-24 21:55:34 |
 Deriváljuk az integrált az x paraméter szerint, majd használjuk a jól ismert 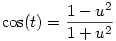 helyettesítést, ahol u=tan (t/2). Ekkor az u változó szerint egy racionális törtfüggvényt kapunk, aminek van elemi primitív függvénye. Visszahelyettesítve a t változót az alábbit kapjuk: helyettesítést, ahol u=tan (t/2). Ekkor az u változó szerint egy racionális törtfüggvényt kapunk, aminek van elemi primitív függvénye. Visszahelyettesítve a t változót az alábbit kapjuk:
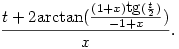
Ennek a megváltozása kell t=0 és t= között. A függvény t=0-ban 0, a t között. A függvény t=0-ban 0, a t  - határesetben pedig x-től függően kétféle értéket vesz fel: vagy nullát vagy 2 - határesetben pedig x-től függően kétféle értéket vesz fel: vagy nullát vagy 2 /x-et. Már csak x szerint kell a primitív függvényt visszakeresni, ami persze triviális. (Az x=0, x=1, x=-1 eseteket persze külön meg kell vizsgálni az eredeti határozott integrálban.) /x-et. Már csak x szerint kell a primitív függvényt visszakeresni, ami persze triviális. (Az x=0, x=1, x=-1 eseteket persze külön meg kell vizsgálni az eredeti határozott integrálban.)
Végeredmény: az eredeti integrál értéke 0, ha -1 x x 1, míg 2 1, míg 2 log |x|, ha x>1 vagy x<-1. log |x|, ha x>1 vagy x<-1.
|
| Előzmény: [1947] Cckek, 2007-03-24 19:44:40 |
|
| [1947] Cckek | 2007-03-24 19:44:40 |
 312.feladat Ha már integráloknál tartunk:
Számítsuk ki a következő integrált:
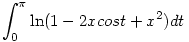
|
|
|
| [1945] Lóczi Lajos | 2007-03-20 03:00:23 |
 311. feladat. Mekkora a tangensfüggvény négyzetgyökének görbe alatti területe 0 és  /4 között? /4 között?
|
|






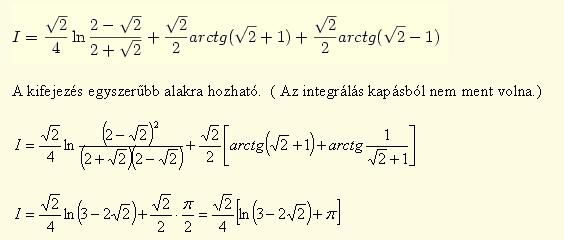
 között. A függvény t=0-ban 0, a t
között. A függvény t=0-ban 0, a t
 x
x