| [1982] Sirpi | 2007-04-17 16:04:29 |
 Hát így kapásból log2k elég, és annyi kell is, mert a 2-hatványokat mind külön kupacba kell rakni. Bocs a gyors lelövésért (nem is írom le a teljes konstrukciót), nem ismertem, csak gyorsan végiggondoltam :-) Jó feladat amúgy.
|
| Előzmény: [1981] Yegreg, 2007-04-17 14:38:30 |
|
| [1981] Yegreg | 2007-04-17 14:38:30 |
 Egy egyszerű, de szerintem érdekes feladat (ami úgy "jutott eszembe", hogy egy másik feladatot rosszul olvastam el :) )
Adottak az 1, 2, ... k számok. Legalább hány csoportba kell osztani őket, hogy ne legyen egy csoportban sem osztó-többszörös?
|
|
| [1980] Lóczi Lajos | 2007-04-17 10:02:58 |
 i-gen, hiszen 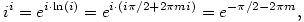 ahol m tetszőleges egész. ahol m tetszőleges egész.
Persze i ellentettje éppúgy jó. (Ezután azt a kérdést tettem fel magamnak, van-e még ezeken kívül ilyen tulajdonságú komplex szám. Azt találtam, hogy végtelen sok van, de csak megszámlálható, a valós részüket egy egyszerű képlet megadja, a képzetes részüket meg egy kicsit bonyolultabb. Akinek van kedve, keresse meg ezeket a "rácspontokat" a síkon.)
|
| Előzmény: [1979] ágica, 2007-04-17 07:53:44 |
|
|
|
| [1977] Lóczi Lajos | 2007-04-15 20:10:22 |
 Szerintem nem, pl. a k=0 esetben rögtön valós lesz z, amit kizártunk. De mondjuk a k=1, a= esetén kapott z:= esetén kapott z:= +i +i tg (1) sem lesz jó, hiszen tetszőleges m egész szám esetén fennáll, hogy tg (1) sem lesz jó, hiszen tetszőleges m egész szám esetén fennáll, hogy
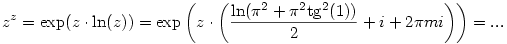
Itt véve pl. az m=0 esetet a következő számot kapjuk:
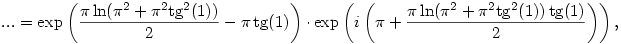
ami sajnos nem valós.
|
| Előzmény: [1976] Cckek, 2007-04-15 12:03:09 |
|
|
| [1975] Lóczi Lajos | 2007-04-12 22:53:58 |
 [100 ]. feladat. Adjunk példát olyan x komplex, de nem valós számra, hogy xx minden értéke valós. ]. feladat. Adjunk példát olyan x komplex, de nem valós számra, hogy xx minden értéke valós.
|
|
|
|
|
|
|
| [1969] Alma | 2007-04-12 18:14:51 |
 Nekem is valami hasonló jött ki, csak én megkaptam a végtelen sok megoldást. Nem kell sokat változtatni az előző megoldáson, csak egy icipicit: a) 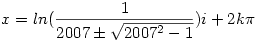 A b) eseten még nem gondolkoztam. A b) eseten még nem gondolkoztam.
|
| Előzmény: [1968] Lóczi Lajos, 2007-04-12 13:53:55 |
|
|
|
|
| [1965] Lóczi Lajos | 2007-04-11 22:22:31 |
 313. feladat. Adjuk meg az összes olyan x (komplex) számot, amelyre
a.) cos (x)=2007
b.) 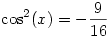 . .
|
|
|
| [1963] Cckek | 2007-04-09 10:40:38 |
 Kellemes ünnepeket mindenkinek.
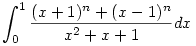 mely n-re racionális? mely n-re racionális?
|
|
| [1962] Cckek | 2007-04-06 07:35:31 |
 Ha már algebrai strukturáknál tartunk... Legyen A egy 4 elemű gyűrű. A akkor és csak akkor test ha az x2+x+1=0 egyenletnek van egy gyöke A-ban.
|
|
|
| [1960] Lóczi Lajos | 2007-04-02 01:28:13 |
 (Még néhány ilyen típusú, érdekes feladatot illetően l. pl. Szendrei-Czédli-Szendrei: Absztrakt algebrai feladatok, JATEPress, 1993. Az itteni feladat amúgy a Gyűrűk fejezet 15. feladatában szerepel.)
|
| Előzmény: [1959] nadorp, 2007-04-01 18:31:09 |
|
| [1959] nadorp | 2007-04-01 18:31:09 |
 Először oldjunk meg egy egyszerűbbet, nevezetesen: Ha egy gyűrűben 1-ab invertálható, akkor 1-ba is az. Megoldás:
Feltehető, hogy sem "a" sem "b" nem a zéróelem. Legyen (1-ab)c=1, azaz abc=c-1. Ekkor
babc=bc-b
babca=bca-ba
ba=bca-babca=(1-ba)bca
1-ba=1-(1-ba)bca. Tehát
(1-ba)(1+bca)=1, azaz 1-ba jobb inverze 1+bca. Hasonlóan adódik a bal inverzre is ugyanez az érték.
Mivel (xy)2=x(yxy) és (yx)2=(yxy)x ezért ha 1-(xy)2 inverze c, akor az előzőek szerint 1-(yx)2 inverze 1+yxycx
|
| Előzmény: [1956] Cckek, 2007-03-31 20:27:37 |
|
|






 esetén kapott z:=
esetén kapott z:=
 Z :)
Z :)