|
| [1993] jonas | 2007-04-18 20:54:31 |
 Akkor megpróbálom mégegyszer elmondani, de még mindig szemléletesen, pontos indukciós feltétel nélkül.
Nyilván csak azokkal a számtani sorozatokkal kell foglalkozni, amiknek a kezdőeleme, és a differenciája is természetes szám (és az utóbbi nem nulla). Ilyen számtani sorozatból csak megszámlálható sok van, valahogy tehát sorba rendezzük őket úgy, hogy mindegyiket hozzárendeljük  egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n  -ra. -ra.
Utána a két halmazt lépésenként konstruáljuk meg úgy, hogy kiindulunk az A0={} és B0={} üres halmazokból, és bővítjük őket, amíg végül teljesítik a feltételeket. Azt szeretnénk elérni, hogy egyik halmaznak se legyen teljes egészében része valamelyik a fenti számtani sorozatokból, amit úgy érhetünk el, hogy minden számtani sorozatból berakunk egy elemet az A halmazba, és egyet a B halmazba. Ez elég, mert a két halmaz végig diszjunkt lesz.
Így aztán a következőképpen járunk el. Ha már megvan az An és Bn halmaz, akkor ezekből az An+1 és Bn+1 halmazokat egy-egy természetes szám hozzáadásával kapjuk meg, a két számot pedig úgy választjuk ki, hogy (1) mindkettő benne legyen az Sn számtani sorozatban, (2) különbözzenek egyástól és az An Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An Bn véges, így még mindig végtelen sok szám marad nekünk, amelyek közül kettőt ki kell választani. Bn véges, így még mindig végtelen sok szám marad nekünk, amelyek közül kettőt ki kell választani.
Például tegyük fel, hogy A1={0},B1={1},A2={0,2},B2={1,3}. Utána S2={0+2k}={0,2,4,6,8,....} amiből ki kell válsztanunk két olyan elemet, ami az A2 B2-ben nincs benne, ezek lehetnek a 4 és a 6, így aztán A3={0,2,4},B3={1,3,6} stb. B2-ben nincs benne, ezek lehetnek a 4 és a 6, így aztán A3={0,2,4},B3={1,3,6} stb.
Miután így minden n  -ra megkaptuk az An és Bn halmazokat, legyen A*= -ra megkaptuk az An és Bn halmazokat, legyen A*= nAn és B*= nAn és B*= nBn. Ez a két halmaz diszjunkt, és mindkettő tartalmaz legalább egy elemet minden érdekes számtani sorozatból. Az viszont még nem feltétlenül teljesül, hogy együtt minden természetes számot tartalmaznának (noha úgy is könnyen végre lehetne hajtani az indukciós lépést, hogy ez is teljesüljön), ezért legyen A= nBn. Ez a két halmaz diszjunkt, és mindkettő tartalmaz legalább egy elemet minden érdekes számtani sorozatból. Az viszont még nem feltétlenül teljesül, hogy együtt minden természetes számot tartalmaznának (noha úgy is könnyen végre lehetne hajtani az indukciós lépést, hogy ez is teljesüljön), ezért legyen A= -B* és B=B*. Mivel A* -B* és B=B*. Mivel A* A és B* A és B* B, ezért továbbra is mindkét halmazban van minden sorozatból elem, viszont az is igaz, hogy A B, ezért továbbra is mindkét halmazban van minden sorozatból elem, viszont az is igaz, hogy A B= B= és A és A B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket. B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket.
|
| Előzmény: [1989] Csimby, 2007-04-18 17:08:10 |
|
| [1992] SAMBUCA | 2007-04-18 20:45:34 |
 Na most hátha:)
(1)(4,5,6)(11,12,13,14,15)(22,23,24,25,26,27,28)...
(2,3)(7,8,9,10)(16,17,18,19,20,21)(29,30,31,32,33,34,35,36)...
azaz 1 ide, 2 oda, 3 ide, ...
|
| Előzmény: [1985] Csimby, 2007-04-18 02:23:52 |
|
|
|
| [1989] Csimby | 2007-04-18 17:08:10 |
 Biztosan bennem van a hiba, de nem teljesen értem a megoldásodat. Mindenesetre meg lehet adni két konkrét halmazt melyekről rögtön látszik hogy jók. És Sirpinek igaza van :-)
|
| Előzmény: [1987] jonas, 2007-04-18 08:09:56 |
|
| [1988] Yegreg | 2007-04-18 16:53:38 |
 érdekes, Sirpi konstrukciója sokkal természetesebb, mint az enyém, nekem eszembe sem jutott, de akkor már leírom az enyémet is: a számok kanonikus alakjában a prímkitevők összege szerint csoportosítunk. Így elég [log2(n)]+1 csoport, és nyilván nem lesz egy csoportban osztó és többszörös.
|
|
| [1987] jonas | 2007-04-18 08:09:56 |
 315. Persze, hogy fel lehet. Csak egy kis indukció kell hozzá.
Felsorolod az összes (nem konstans) végtelen számtani sorozatot, ami természetes számokból áll. Ilyenből persze csak megszámlálható sok van. Sorba mész rajtuk, és mindegyikből egy elemet beraksz az első halmazba, aztán egyet a második halmazba. Mivel úgy csináltad a felsorolást, hogy mindegyik számtani sorozat előtt csak véges sok másik van, csak véges sok számról döntöttél véglegesen, tehát van még két olyan szám, amivel el tudod rontani a soron jövő sorozatot. Végül a maradék természetes számokat berakod az első halmazba.
|
| Előzmény: [1985] Csimby, 2007-04-18 02:23:52 |
|
|
| [1985] Csimby | 2007-04-18 02:23:52 |
 [100 ]+1. feladat Fel lehet-e bontani a természetes számok halmazát két részhalmazra úgy, hogy egyikben se legyen végtelen számtani sorozat? ]+1. feladat Fel lehet-e bontani a természetes számok halmazát két részhalmazra úgy, hogy egyikben se legyen végtelen számtani sorozat?
|
|
| [1984] Sirpi | 2007-04-17 23:55:41 |
 Konstrukió (lehet máshogy amúgy?):
{1},{2,3},{4,5,6,7},{8,9,10,11,12,13,14,15}...
|
| Előzmény: [1983] Yegreg, 2007-04-17 17:05:52 |
|
| [1983] Yegreg | 2007-04-17 17:05:52 |
 semmi baj, tényleg gyorsan meg lehet oldani, viszont valóban a konstrukció az érdekesebb része, kíváncsi vagyok, hogy ti is azt a konstrukciót adjátok-e, mint én találtam
|
|
| [1982] Sirpi | 2007-04-17 16:04:29 |
 Hát így kapásból log2k elég, és annyi kell is, mert a 2-hatványokat mind külön kupacba kell rakni. Bocs a gyors lelövésért (nem is írom le a teljes konstrukciót), nem ismertem, csak gyorsan végiggondoltam :-) Jó feladat amúgy.
|
| Előzmény: [1981] Yegreg, 2007-04-17 14:38:30 |
|
| [1981] Yegreg | 2007-04-17 14:38:30 |
 Egy egyszerű, de szerintem érdekes feladat (ami úgy "jutott eszembe", hogy egy másik feladatot rosszul olvastam el :) )
Adottak az 1, 2, ... k számok. Legalább hány csoportba kell osztani őket, hogy ne legyen egy csoportban sem osztó-többszörös?
|
|
| [1980] Lóczi Lajos | 2007-04-17 10:02:58 |
 i-gen, hiszen 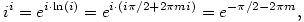 ahol m tetszőleges egész. ahol m tetszőleges egész.
Persze i ellentettje éppúgy jó. (Ezután azt a kérdést tettem fel magamnak, van-e még ezeken kívül ilyen tulajdonságú komplex szám. Azt találtam, hogy végtelen sok van, de csak megszámlálható, a valós részüket egy egyszerű képlet megadja, a képzetes részüket meg egy kicsit bonyolultabb. Akinek van kedve, keresse meg ezeket a "rácspontokat" a síkon.)
|
| Előzmény: [1979] ágica, 2007-04-17 07:53:44 |
|
|
|
| [1977] Lóczi Lajos | 2007-04-15 20:10:22 |
 Szerintem nem, pl. a k=0 esetben rögtön valós lesz z, amit kizártunk. De mondjuk a k=1, a= esetén kapott z:= esetén kapott z:= +i +i tg (1) sem lesz jó, hiszen tetszőleges m egész szám esetén fennáll, hogy tg (1) sem lesz jó, hiszen tetszőleges m egész szám esetén fennáll, hogy
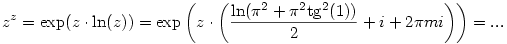
Itt véve pl. az m=0 esetet a következő számot kapjuk:
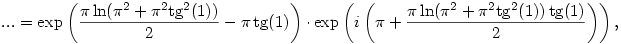
ami sajnos nem valós.
|
| Előzmény: [1976] Cckek, 2007-04-15 12:03:09 |
|
|
| [1975] Lóczi Lajos | 2007-04-12 22:53:58 |
 [100 ]. feladat. Adjunk példát olyan x komplex, de nem valós számra, hogy xx minden értéke valós. ]. feladat. Adjunk példát olyan x komplex, de nem valós számra, hogy xx minden értéke valós.
|
|
|
|
|
|
|




 k
k

 egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n
egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n
 Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An
Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An A és B*
A és B* B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket.
B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket. 




