|
| [2068] BohnerGéza | 2007-05-09 00:12:34 |
 Mutassuk meg, hogy tetszőleges n pozitív egészre van n db pithagóraszi számhármas, melyekben az átfogó (vagy az egyik befogó) megegyezik!
|
|
|
|
|
| [2064] Gubbubu | 2007-05-08 15:46:12 |
 A negyedik egyértelműen egy halászbárka, amelyet egy 200 méter magas hullám épp a csúcsára vett. A másik három vízijármű egy 200 méter oldalhosszúságú egyenlőszárú háromszög három csúcsát alkotja, melyek mindegyike 200 méter távolságra van a halászbárkától.
A "tengeralattjáró" kifogásolható megoldás, mivel nem a szó szoros értelmében a "tengeren" halad, hanem a tenger>ben< (kivéve persze, ha épp felszíni üzemmódban halad. De akkor meg nem a szó szoros értelmében vett tengeralattjáró, hanem tengeralattjáró, amelyet halászbárkának használnak).
Ez az egzakt megoldás.
|
| Előzmény: [2051] Fálesz Mihály, 2007-05-04 10:47:19 |
|
| [2063] Cckek | 2007-05-06 18:29:46 |
 324.feladat Határozzuk meg azon n-edrendű permutációk számát melyekre |p(i)-i| i i
|
|
|
|
| [2060] Lóczi Lajos | 2007-05-05 01:03:05 |
 Pár kérdés, amit nem értek:
1. Miért lenne log j=j /4 ? Szerintem nem az. /4 ? Szerintem nem az.
2. Valósban sem a kitevő, hanem az alap logaritmusát vesszük egy hatvány definíciójakor, tehát nem jó formulából indulsz ki.
3. exp(k /4) értéke nem k. /4) értéke nem k.
|
| Előzmény: [2059] jonas, 2007-05-04 22:53:31 |
|
| [2059] jonas | 2007-05-04 22:53:31 |
 Jó kérdés.
Azt ugye tudjuk, hogy log j=j /4, így azt mondhatnánk, hogy ij=exp(ilog j)=exp(ij /4, így azt mondhatnánk, hogy ij=exp(ilog j)=exp(ij /4)=exp(k /4)=exp(k /4)=k. Viszont ugyanígy mondhatnánk, hogy ij=exp(log j.i)=-k. Nem tudom, melyik a helyes, és egyáltalán azt sem, hogy értelmezve van-e a hatvány. /4)=k. Viszont ugyanígy mondhatnánk, hogy ij=exp(log j.i)=-k. Nem tudom, melyik a helyes, és egyáltalán azt sem, hogy értelmezve van-e a hatvány.
Az előző e alapú hatvány azért volt értelmezve, mert egy valós együtthatós hatványsorba bármilyen kvaternió elemet (vagy mátrixot) be tudunk helyettesíteni, hiszen egy elem hatványai felcserélhetőek egymással és a komplex számokkal is. Ezzel szemben az ix már nem valós, hanem komplex együtthatós hatványsor, amibe pedig nem helyettesíthetünk be akármilyen kvaterniót. Ha j-t az előzőhez hasonlóan egy 4x4-es valós mátrixként fogjuk fel, és behelyettesítjük a komplex hatványsorba, akkor egy nem valós komplex mátrixot kapunk, amit nem foghatunk fel kvaternióként.
|
| Előzmény: [2050] Lóczi Lajos, 2007-05-03 22:15:57 |
|
|
| [2057] Yegreg | 2007-05-04 16:24:05 |
 Igazoljuk, hogy ha x1,x2,...,xn pozitív számok, akkor 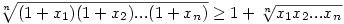 ! !
|
|
|
|
| [2054] HoA | 2007-05-04 13:48:37 |
 Attól még nem hibás egy feladat, hogy több megoldása van. Ha a kitűző azt szeretné, hogy csak egy legyen, szigorítsa a feltételeket. Tehát a 324. feladatra rímelő kitűzés: Hogyan lehet 6 gyufaszálból 4 olyan szabályos háromszöget kirakni, melyek oldala egy gyufaszál hosszú ?
|
| Előzmény: [2053] jonas, 2007-05-04 13:25:40 |
|
|
|
| [2051] Fálesz Mihály | 2007-05-04 10:47:19 |
 324. feladat. Négy hajó halad a tengeren, bármelyik kettő távolsága pontosan 200 méter. Az egyik egy motorcsónak, a második egy jacht, a harmadik vitorlás hajó. Milyen hajó a negyedik?
|
|
| [2050] Lóczi Lajos | 2007-05-03 22:15:57 |
 Akkor most már elő van készítve a terep, hogy kiszámoljuk,
323. feladat. Mennyi a kvaterniók körében ij? (Mivel nálam rosszul olvasható: "i a j-ediken".)
|
|
|
|
| [2047] jonas | 2007-05-03 15:58:36 |
 A másik lehetőség a megoldásra az, hogy a kvaterniók gyűrűjét egy mátrixgyűrűként reprezentáljuk:
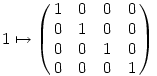
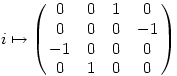
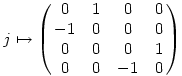
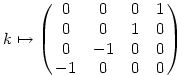
Így
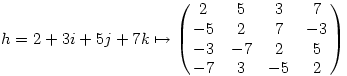
Amin pedig a szokásos módon elvégezhetjük az exponenciálást (ezt elvileg zárt képlettel is ki lehetne fejezni, mert a mátrix 4x4-es, tehát a sajátértékeket legfeljebb negyedfokú egyenlet megoldásaként kaphatjuk). Így aztán az eredmény
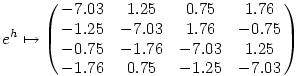
Ezt pedig csak ki kell fejezni az 1,i,j,k-nak megfelelő mátrixok kombinációjaként, és megkapjuk, hogy eh=-7.03+0.75i+1.25j+1.76k.
|
|
|
| [2045] Lóczi Lajos | 2007-05-03 00:53:09 |
 Még mindig nem egészen értem. Amikor pl. levezetjük az eix=cos (x)+isin (x) összefüggést, akkor vajon használjuk-e az i2=-1 tulajdonságot? Ha igen, akkor nem látom, hogy i helyett m-et írva ennek helyessége hogyan marad meg, ha egyszer m2 -1. -1.
|
| Előzmény: [2043] jonas, 2007-05-03 00:40:04 |
|






 i
i
 /4 ? Szerintem nem az.
/4 ? Szerintem nem az. 






 -1.
-1.