| [1452] jenei.attila | 2004-01-06 10:55:56 |
 Sziasztok!
A 41.feladat megoldása
A feltételekből következik, hogy p|ab+ac+ad+ae+bc+bd+be+cd+ce+de -nek. A szimmetrikus polinomok alaptétele szerint mindem szimmetrikus polinom előáll elemi szimmetrikus polinomok polinomjaként. Ez alapján:
a5+b5+c5+d5+e5=5abcde+(a+b+c+d+e)5-
-5(a+b+c+d+e)3(ab+ac+bc+ad+bd+cd+ae+be+ce+de)+5(a+b+c+d+e)(ab+ac+bc+ad+bd+cd+ae+be+ce+de)2+
+5(a+b+c+d+e)2(abc+abd+acd+bcd+abe+ace+bce+ade+bde+cde)-
-5(ab+ac+bc+ad+bd+cd+ae+be+ce+de)(abc+abd+acd+bcd+abe+ace+bce+ade+bde+cde)-
-5(a+b+c+d+e)(abcd+abce+abde+acde+bcde)
. Innen már látszik a feladat állítása.
|
| Előzmény: [182] Pach Péter Pál, 2003-12-08 20:18:19 |
|
| [205] GJ | 2004-01-05 19:35:20 |
 46.feladat p prím,tehát 3-mal osztva 1 vagy 2 maradékot ad tehát ha p maradéka 1 (3-mal osztva)->p+2 maradéka (3-mal osztva) 0->p+2 nem prím hasonlóan ha p maradéka 3-mal osztva 2,akkor p-2 maradéka 0(3-mal soztva)->p-2 nem prím
vagyis nincs az 5-ön kívül ilyen p prím
|
| Előzmény: [204] Gubbubu, 2004-01-05 19:22:37 |
|
| [204] Gubbubu | 2004-01-05 19:22:37 |
 Üdvözlök mindenkit!
A két ünnep között egy nap azzal szórakoztam, hogy a természetes számok során valameddig végigmenve a számokat különféle nevezetes sorozatokba soroltam. Ennek során egész érdekes, könnyebb-nehezebb problémákra bukkantam, sokat egyáltalán nem tudok vagy nincs időm megoldani, de hátha másokat érdekel. Néhány példa:
46. feladat:
Van-e olyan p prím az 5-ön kívül, amelyre p-2, p és p+2 is prím? Keressünk minél többet, vagy lássuk be hogy nincs.
47. feladat:
Lássuk be vagy cáfoljuk meg, hogy 6 az egyetlen szám (poz. egész, egész, rac., valós vagy komplex), amely ugyanazon számtani sorozat elemeinek egyszerre az összege és a szorzata!
47. feladat:
Oldjuk meg a n2+1=2n egyenletet!
Egyenlőre ennyi.
(Várhatóan hétvégén jövök újra, addig megoldani!)
|
|
| [203] jenei.attila | 2004-01-05 15:27:03 |
 Kedves István!
A Te megoldásoddal az a baj, hogy miközben az x végigmegy a megfelelő egész számokon, nem biztos, hogy 1-től egyesével növekedve kapjuk a számokat [P/Q*x]-ből, hanem a sorozatban az egymás utáni tagok [P/Q]-val, vagy [P/Q]+1 -gyel növekszenek.
Vegyük a derékszögű koordináta rendszerben a P/Q meredekségű, origón áthaladó egyenest, és tekintsük az x=1, y=1, és x=[Q/2], y=[P/2] egyenesek által határolt téglalapot. Ekkor a bizonyítandó egyenlőség mindkét oldala, a téglalapban található rácspontok (mindkét koordinátája egész) számát adja (a határokat is beleértve). Ugyanis [P/Q*x] az x-en áthaladó függőleges egyenesen fekvő, P/Q meredekségű egyenes alatti, a szóbanforgó téglalapba eső rácspontok száma. Ha x végigfut a megfelelő egész számokon, nyilván megkapjuk az összes, téglalapba eső, P/Q meredekségű egyenes alatti rácspontok számát. A másik szumma ugyanígy az egyenes feletti rácspontok számát adja. A feltételek biztosítják, hogy nem esik rácspont a P/Q meredekségű egyenesre, így minden pontot csak egyszer számolunk. Márészt a jobboldali kifejezés közvetlenül a téglalapban fekvő rácspontok számát adja.
|
| Előzmény: [194] lorantfy, 2003-12-17 23:58:40 |
|
|
|
|
| [199] lorantfy | 2003-12-29 14:48:13 |
 44. feladat: Arkhimédész "problema bovinum"-a (kb. 2222 éves faladat!) Volt a Napistennek egy bikákból és tehenekből álló csordája, amelyiknek egyik része fehér, egy másik része fekete, egy harmadik része tarka és egy negyedik része barna marhákból állt. A fehér bikák száma a fekete bikák számának felével meg egyharmadával volt több, mint a barna bikáké, a feketéké a tarka bikák számának negyedével meg ötödével, a tarkáké pedig a fehérek számának egyhatodával meg egyhetedével. A fehér tehenek száma az összes fekete marhák számának egyharmada meg egynegyede volt, a fekete tehenek száma az összes tarka marhák számának egynegyede meg egyötöde, a tarka tehenek száma az összes barna marhák számának egyötöde meg egyhatoda, a barna tehenek száma az összes fehér marha számának egyhatoda meg egyhetede. Hogyan tevődött össze a csorda a különböző színű állatokból?
Szilveszter utáni önteszthez ajánlom ezt a feladatot! (Magamhoz tértem-e már?)
(A feladat Heinrich Dörrie: A DIADALMAS MATEMATIKA c. könyvében található.)
|
|
|
| [197] Ratkó Éva | 2003-12-18 16:18:12 |
 34. feladat: Jártam a színházban, és beszéltem egy jegyszedövel is, aki természetesen tiltakozott. Szerinte csak véletlenül nem tudtak visszaadni. Annyit megtudtam, hogy 1000 Ft apróval indítják útnak a jegyszedöket, illetve 450 és 650 Ft-os árai vannak a füzeteknek (ennyi jutott akkor eszébe, persze lehet, hogy van más ár is). Így azt a kérdést tudjuk feltenni, hogy hány füzetet tud egy jegyszedö eladni legalább p valószínüséggel. És ha nem akarunk teljesen sötétségben tapogatózni, valamiféle felmérést kellene végezni arról, hogy milyen valószínüséggel van valakinél apró (ezt természetesen alaposan átgondolt kérdések formájában).
|
|
| [196] lorantfy | 2003-12-18 12:42:47 |
 Kedves Géza!
Köszönet a segítségért! Közben rájöttem, hogy ennyire egyszerű a megoldás. Gondolkodom a 34.c-n. Sajnos a Catalan-számokról fogalmam sincs. Akinek van segíthet!
Pontosítás az előző hozzászólásomhoz:
A 42. feladatról van szó!
|
| Előzmény: [195] Kós Géza, 2003-12-18 10:52:47 |
|
|
| [194] lorantfy | 2003-12-17 23:58:40 |
 41. feladathoz: Legyen P=2p+1 és Q=2q+1, ahol p,q pozitív egész számok.
Ekkor a jobb oldal:
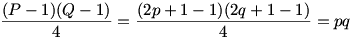
Bal oldalon az első szumma, miközben x végigsöpör az adott intervallumon, előállítja az egész számok összegét 1-től p-ig.
![\sum_{0<x<\frac{Q}{2}}{\left[\frac{Px}{Q}\right]}=1+...+
\left[\frac{(2p+1)(2q+1)}{(2q+1)2}\right]=1+...+\left[p+\frac{1}{2}\right]=1+...+p= \frac{p^2+p}{2}](keplet.cgi?k=D15D442F290673AF)
Hasonlóan a második szumma is. Így a bal oldal: 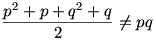
(P=3, Q=5 esetén 1+2 2) 2)
Szóval itt valami baj van. Lehet, hogy tévedek, de valaki legalább hozzászól!
|
| Előzmény: [182] Pach Péter Pál, 2003-12-08 20:18:19 |
|
| [193] lorantfy | 2003-12-13 11:00:24 |
 34.c) feladat b része
Ha a füzeteket áruló néni előrehívja azt az „x” számú embert aki 500 Ft-al tud fizetni, akkor miután eladta nekik a füzetet (k+x) 500Ft-os bankjegye lesz, hogy visszaadjon a megmaradó (n-x) 1000 Ft-al fizetőnek. Mikor nem tud visszaadni? Ha
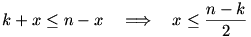
(Egyenlőség NINCS, csak nem találok külön kisebb jelet! Segítség!)
Legyen 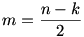 (Elnézést! Az előző hozzászólásban ezt rosszul írtam!) (Elnézést! Az előző hozzászólásban ezt rosszul írtam!)
Tehát, ha az n ember közül csak 0,1,2 … m-1 tud 500 Ft-al fizetni, akkor nem tud a néni visszaadni. Ezen esetek összege:
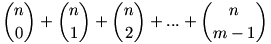
A p2 valószínűség, (2n az összes esetek száma)
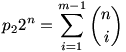
Tehát p1=2p2
|
| Előzmény: [192] lorantfy, 2003-12-12 23:59:35 |
|
| [192] lorantfy | 2003-12-12 23:59:35 |
 Kedves Fórumosok!
Érdemes "beleélni" magatokat ebbe a füzeteladási feladatba, mert bár lassan de szépen alakul.
Próbáljuk megfogalmazni a bináris fa alapján készült előző táblázat eredményét általánosan.
k db 500 Ft van kezdetben az eladónál és n emberünk van.
Legyen az egyszerűbben írhatóság kedvéért k és n páros!
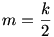 , E= az eladott könyvek száma, S=esetek száma. , E= az eladott könyvek száma, S=esetek száma.
| E= |
... |
k |
k+1 |
k+2 |
k+3 |
... |
n-4 |
n-3 |
n-2 |
n-1 |
n |
| S= |
0 |
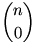 |
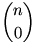 |
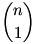 |
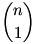 |
|
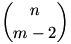 |
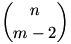 |
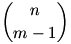 |
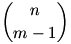 |
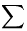 |
|
Az, hogy a néni valamikor nem tud visszaadni azt jelenti nem adott el minden könyvet. Ezen esetek számának összege:

Megvan a 34.c) feladat a) részének p1 valószínűsége.
Már csak azt kell belátni, hogy
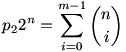
de erre már csak holnap kerülhet sor. :-)
|
| Előzmény: [191] lorantfy, 2003-12-12 00:48:45 |
|
| [191] lorantfy | 2003-12-12 00:48:45 |
 Kedves Fórumosok!
Egy rövid folytatásra futotta ma az időmből, remélve, hogy lesz aki bekapcsolódik.
Ha k értékét 1-el növeljük akkor azon esetekben, ahol eddig 0 db-ot adtunk el, most 1-et fogunk, ahol eddig 1-et, most 2 db-ot adunk el... Az esetek száma 1-el nagyobb db-számra tolódik el. n= 5 esetében ezt mutatja a táblázat. Az 5-ös eladás oszlopában összegződnek a jobbra tolódó értékek. Jobb oldalon annak a valószínüsége  , hogy minden (5db) könyvet eladtunk. (Az esetek számával (25=32) osztottam az 5 db-os eladások számát.)Annak valószinüsége, hogy a néni valamikor nem tudott visszaadni 1- , hogy minden (5db) könyvet eladtunk. (Az esetek számával (25=32) osztottam az 5 db-os eladások számát.)Annak valószinüsége, hogy a néni valamikor nem tudott visszaadni 1- , hiszen akkor nem adott el minden könyvet. Tehát csak ezt kell n-re megfogalmazni és megvan Géza 34.c) feladatának a) része! , hiszen akkor nem adott el minden könyvet. Tehát csak ezt kell n-re megfogalmazni és megvan Géza 34.c) feladatának a) része!
| k |
0 |
1 |
2 |
3 |
4 |
5 |
 |
| 0 |
1 |
1 |
5 |
5 |
10 |
10 |
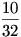 |
| 1 |
0 |
1 |
1 |
5 |
5 |
20 |
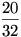 |
| 2 |
0 |
0 |
1 |
1 |
5 |
25 |
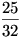 |
| 3 |
0 |
0 |
0 |
1 |
1 |
30 |
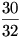 |
| 4 |
0 |
0 |
0 |
0 |
1 |
31 |
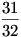 |
| 5 |
0 |
0 |
0 |
0 |
0 |
32 |
1 |
|
|
| Előzmény: [186] lorantfy, 2003-12-10 13:41:47 |
|
|
| [189] lorantfy | 2003-12-11 22:40:16 |
 Megoldás a 43. feladatra:
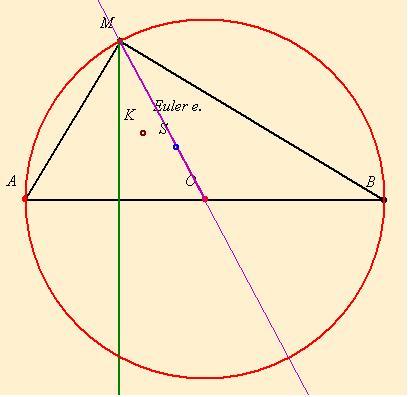
A háromszög körülírt körének O középpontja csak akkor van a háromszög kerületén, ha az derékszögű. Ekkor viszont az M magasságpont a derékszögű csúcsba esik. Így OM = R= AB/2, OM csak a rövidebbik befogóval egyezhet meg. Tehát a háromszög szögei 30-60-90 fok. Szerkesztése: 2OM=AB fölé Thálesz kört, aztán A-ból OM=R-el körözve kimetszük a C pontot. (A feladat szövegében ez áll:„tudjuk, hogy e szakasz egyik végpontja egyben a háromszög egyik pontja is” - ez csak annyit jelent, hogy azt még nem tudjuk, hogy a másik végpontja is (De mostmár tudjuk!), nem pedig azt, hogy a másik végpontja nem lehet a háromszög pontja)
Euler egyenes: A háromszög O, S, M ponjai erre az egyenesre esnek. Ráadásul MS=2OS.
Aki kíváncsi az Euler egyenes nevezetes pontjai és a beírt kör K középpontjának kapcsolatára, nézze meg a „Nehezebb matematikai problémák” témában Rácz Béla 7. feladatát.
|
 |
| Előzmény: [188] Hajba Károly, 2003-12-11 01:06:29 |
|
| [188] Hajba Károly | 2003-12-11 01:06:29 |
 Elnézést, pontosítok:
43. feladat: Legyen adott egy háromszög Euler-féle OM szakasza; tudjuk, hogy e szakasz egyik végpontja egyben a háromszög egyik pontja is ill. a háromszög egyik oldalhossza megegyezik az OM szakasz hosszával. Szerkesszük meg a háromszöget!
HK
|
| Előzmény: [187] Hajba Károly, 2003-12-11 01:03:40 |
|
| [187] Hajba Károly | 2003-12-11 01:03:40 |
 35. feladat: Legyen adott egy háromszög Euler-féle OM szakasza; tudjuk, hogy e szakasz egyik végpontja egyben a háromszög egyik pontja is ill. a háromszög egyik oldalhossza megegyezik az OM szakasz hosszával. Szerkesszük meg a háromszöget!
HK
|
|
| [186] lorantfy | 2003-12-10 13:41:47 |
 Kedves Fórumosok!
Reméltem, hogy valakinek megtetszik ez a bináris fa, de még nem késő! Felírtam a csúcsokhoz az eladások számát. A táblázatban az első oszlopban az n értéke, a következő oszlopokban az áll, hogy adott n esetén hány esetben volt 0,1,2,3,4,5 füzet eladás.
| n |
0 |
1 |
2 |
3 |
4 |
5 |
| 1 |
1 |
1 |
|
|
|
|
| 2 |
1 |
1 |
2 |
|
|
|
| 3 |
1 |
1 |
3 |
3 |
|
|
| 4 |
1 |
1 |
4 |
4 |
6 |
|
| 5 |
1 |
1 |
5 |
5 |
10 |
10 |
|
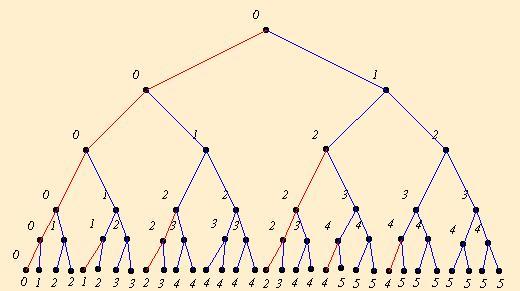
Ezek a számsorok mindenkinek ismerősek (Pascal hrsz. Binomiális tétel) A sorrend kicsit más. Remélhetőleg valaki be is bizonyítja, én most csak ebből a pár értékből általánosítok: Legyen 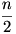 egész része: m. Ekkor a 2n esetből egész része: m. Ekkor a 2n esetből  esetben fogunk n db füzetet eladni k=0 befektettéssel. Következik k értékének 1-el való növelése. Ekkor ennek a fának a jobb oldali (fél) részfájára kell áttérni. esetben fogunk n db füzetet eladni k=0 befektettéssel. Következik k értékének 1-el való növelése. Ekkor ennek a fának a jobb oldali (fél) részfájára kell áttérni.
|
 |
| Előzmény: [184] lorantfy, 2003-12-09 12:37:33 |
|
| [185] Kós Géza | 2003-12-10 13:16:34 |
 Egy kis érdekesség.
Továbbra is feltételezzük , hogy a vendégeknél 50-50% valószínűséggel van egyetlen 500 vagy egyetlen 1000 forintos bankjegy. A vendégek száma n, a jegyszedőnél kezdetben k darab 500 forintos van.
a) A vendégek véletlenszerűen sorbaállnak, fizetnek, a jegyszedő néni visszaad, ha tud. Jelöljük p1-gyel annak a valószínűségét, hogy valamikor nem tud visszaadni.
b) A jegyszedő úgy dönt, hogy a sorban előrehívja azokat, akiknél 500 forintos pénz van. Jelöljük p2-vel annak a valószínűségét, hogy így sem sikerül mindenkinek visszaadni.
34.c feladat. Bizonyítsuk be, hogy ha n és k azonos paritású, akkor p1=2p2.
(A Catalan-számokat jól ismerők előnyben!)
|
| Előzmény: [138] Ratkó Éva, 2003-12-03 14:33:47 |
|
| [184] lorantfy | 2003-12-09 12:37:33 |
 Pontosítás az előzőhöz:
A következő vevőnek 50% eséllyel van 500 Ft-osa és 50%, hogy 1000 Ft-osa van. Ez végig állandó. (Nem függ attól, hányan fizettek már pl. 1000 Ft-al.)
|
| Előzmény: [183] lorantfy, 2003-12-09 01:07:25 |
|
| [183] lorantfy | 2003-12-09 01:07:25 |
 Kedves Éva!
Egy újabb próbálkozás:
34.b feladat
n db füzetet szeretnénk eladni n embernek. A füzet ára 500 Ft. Az emberek felének van 500 Ft-ja, másik felének csak 1000 Ft-osa van.
1.Ha 1000 Ft-al akar fizetni valaki és nincs 500 Ft-unk vissza, akkor nem vesz, ha tudunk visszaadni, akkor vesz.
2.Ha 500 Ft-al fizet valaki, akkor persze vesz füzetet és lesz egy visszaadható 500 Ft-unk.
Mennyi a valószinüsége, hogy mind az n könyvet eladjuk:
1.Ha kezdetben nincs 500 Ft-osunk (k=0)
2.Ha k db 500 Ft-ossal indulunk.
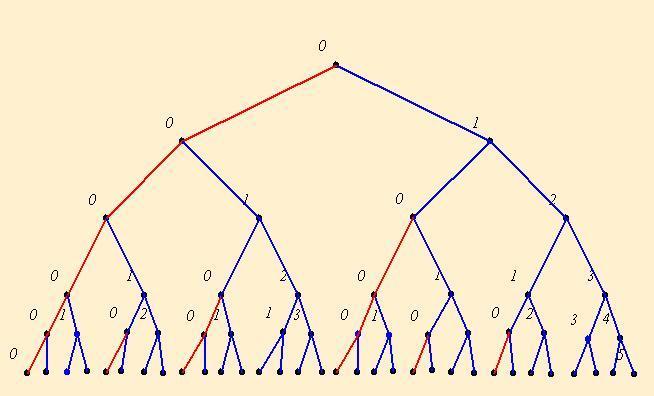
Árázoljuk az eseményeket egy bináris fával. A csúcsokba írjuk az 500 Ft-osaink számát. Az élek szine kék ha vettek, piros, ha nem vettek füzetet. Ha jobbra lépek 500 Ft-al fizettek, ha balra akkor 1000 Ft-al. Piros a vonal, ha nullás pontból balra lépünk, különben kék. Az összes eset száma 2n. Ahány kék vonallal jutunk le, annyi füzetet adtunk el.
Próbáljátok általánosítani! n=5 esetén a következő értékek adódnak:
k=0 : 50%, k=1 : 62,5%, k=2 : 78%, k=3 : 93%, k=4 : 97%, k=5 : 100
|
 |
| Előzmény: [181] Ratkó Éva, 2003-12-08 17:17:54 |
|
| [182] Pach Péter Pál | 2003-12-08 20:18:19 |
 Két újabb feladat:
41. feladat
Legyenek a,b,c,d,e egész számok. Tudjuk, hogy összegük és négyzetösszegük is osztható a páratlan p számmal. Bizonyítsuk be, hogy ekkor a5+b5+c5+d5+e5-5abcde is osztható p-vel.
42. feladat
Legyenek P és Q pozitív páratlan relatív prím számok. Bizonyítsuk be, hogy
![\sum_{0<x<\frac{Q}{2}}{\left[\frac{Px}{Q}\right]}+\sum_{0<y<\frac{P}{2}}{\left[\frac{Qy}{P}\right]}=\frac{(P-1)(Q-1)}{4}.](keplet.cgi?k=13B286BB2A4BD346)
|
|








 2)
2)  , hogy minden (5db) könyvet eladtunk. (Az esetek számával (25=32) osztottam az 5 db-os eladások számát.)Annak valószinüsége, hogy a néni valamikor nem tudott visszaadni 1-
, hogy minden (5db) könyvet eladtunk. (Az esetek számával (25=32) osztottam az 5 db-os eladások számát.)Annak valószinüsége, hogy a néni valamikor nem tudott visszaadni 1-


