 Tudjuk, hogy a megadott X tér Banach-tér. Az U operátor nyilván lineáris.
a.) Az U operátor korlátos az X téren és ||U||op. operátornormája éppen 3/2, hiszen az X tér egységgömbjéről vett tetszőleges x függvénnyel
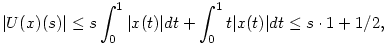
ennek a kifejezésnek a maximuma pedig s [0,1] esetén 3/2, amiből kapjuk, hogy ||U||op. [0,1] esetén 3/2, amiből kapjuk, hogy ||U||op. 3/2. Viszont az x(t) 3/2. Viszont az x(t) 1 választás mutatja, hogy ||U(x)||=3/2 elérhető. 1 választás mutatja, hogy ||U(x)||=3/2 elérhető.
b.) Mivel tetszőleges x X függvény esetén U(x) egy s X függvény esetén U(x) egy s a.s+b alakú X-beli függvény ( a.s+b alakú X-beli függvény (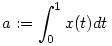 és és 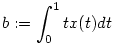 ), ezért az U operátor ranU értékkészlete részhalmaza az elsőfokú polinomok alterének X-ben, ami véges dimenziós. U tehát véges rangú, emiatt kompakt operátor. ), ezért az U operátor ranU értékkészlete részhalmaza az elsőfokú polinomok alterének X-ben, ami véges dimenziós. U tehát véges rangú, emiatt kompakt operátor.
e.) Bármely kompakt operátorra igaz, hogy spektruma csak a sajátértékeiből, illetve legfeljebb a 0 számból állhat. Mivel az X tér most végtelen dimenziós, ismert, hogy a 0 ilyenkor mindig spektrumpont. Megmutatjuk, hogy U-nak csak két nemnulla sajátértéke van.
Ehhez az U(f)= f egyenlet megoldása szükséges: keresendő az összes olyan komplex f egyenlet megoldása szükséges: keresendő az összes olyan komplex   0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely 0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely   0 számok esetén van nemtriviális megoldása az 0 számok esetén van nemtriviális megoldása az
a/3+b/2= b b
a/2+b= a a
egyenletrendszernek. Egyszerűen látszik, hogy ez csak 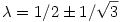 esetén van így, ezek tehát az U operátor nemnulla sajátértékei. esetén van így, ezek tehát az U operátor nemnulla sajátértékei.
U spektruma tehát 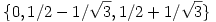 . .
c.) U nem injektív, mert a 0 egyúttal sajátérték is.
d.) A legkevésbé nyilvánvaló állítás a feladatból az, hogy a 0 szám sajátértéke is U-nak. Ehhez olyan f:[0,1] R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis 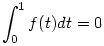 és és  . Ilyet lehet találni, de kíváncsi vagyok, ki milyen példát ad, a végén erre visszatérek. . Ilyet lehet találni, de kíváncsi vagyok, ki milyen példát ad, a végén erre visszatérek.
f.) A kérdés nem a szokásos alakú, de arra nagyon hasonlít: a kitűző véletlenül itt nem a spektrálsugárra gondolt? Az U operátor spektrálsugara nem más, mint a 0-tól legmesszebb lévő pont a kompakt spektrumból, ami jelen esetben 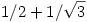 . Ismert, hogy ez a szám egyenlő a . Ismert, hogy ez a szám egyenlő a 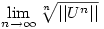 limesszel -- nem elírás az f.) pont és erre gondoltál? (Az eredeti kérdésre egy lineáris rekurzió megoldása után úgy tűnik, könnyen lehetne válaszolni, de azt még nem néztem meg.) limesszel -- nem elírás az f.) pont és erre gondoltál? (Az eredeti kérdésre egy lineáris rekurzió megoldása után úgy tűnik, könnyen lehetne válaszolni, de azt még nem néztem meg.)
g.) Jelölje Id az X tér identitásoperátorát. A válasz igen, hiszen az (U-1.Id) operátor (az X X korlátos lineáris operátorok Banach-terében) invertálható, lévén az 1 nem spektrumpont. (Sőt, emiatt több is igaz: fennáll a kezdeti feltételtől való folytonos függés is.) X korlátos lineáris operátorok Banach-terében) invertálható, lévén az 1 nem spektrumpont. (Sőt, emiatt több is igaz: fennáll a kezdeti feltételtől való folytonos függés is.)
h.) Az 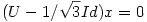 egyenletnek csak az x azonosan 0 függvény a megoldása, mert egyenletnek csak az x azonosan 0 függvény a megoldása, mert 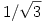 nem spektrumpont, innentől pedig l. az előbbi pontot. nem spektrumpont, innentől pedig l. az előbbi pontot.
Végül visszatérve a fent említett kérdésre, oldjuk meg az alábbi feladatot:
Adjunk példát olyan f:[0,1] R folytonos függvényre, ami nem azonosan nulla, de tetszőleges elsőfokú p polinommal R folytonos függvényre, ami nem azonosan nulla, de tetszőleges elsőfokú p polinommal 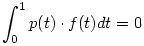 . .
| 



 R differenciálható, mindenütt pozitív, f'(x)=f(f(x)). (Úgy emlékszem, nincs megoldása, de utánanézhetek, ha kell.)
R differenciálható, mindenütt pozitív, f'(x)=f(f(x)). (Úgy emlékszem, nincs megoldása, de utánanézhetek, ha kell.) 

 R számokat úgy hogy
R számokat úgy hogy 



 x
x 3/2. Viszont az x(t)
3/2. Viszont az x(t) 1 választás mutatja, hogy ||U(x)||=3/2 elérhető.
1 választás mutatja, hogy ||U(x)||=3/2 elérhető.  a.s+b alakú X-beli függvény (
a.s+b alakú X-beli függvény ( f egyenlet megoldása szükséges: keresendő az összes olyan komplex
f egyenlet megoldása szükséges: keresendő az összes olyan komplex  0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely
0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely 