|
| [2118] Csimby | 2007-07-02 13:37:44 |
 (reciprok képzés, 1-x, nem vezet ki közülük, viszont ezeknek mind szerepelnie kell) Kéne még vacakolni hogy mi van ha egybeesik pár. De úgy emlékszem algerba gyakorlaton volt valami hasonló Galois elmélet keretein belül. Majd ha végeztem a diffegy vizsgával és lesz időm megkeresem :-)
|
| Előzmény: [2117] Csimby, 2007-07-02 13:31:30 |
|
|
| [2116] Cckek | 2007-07-02 12:48:26 |
 Szép:) Amúgy ezek második fokozati vizsgakérdések itt Romániában. Itt van még egy ha érdekel valakit:
Határozzuk meg azokat az ötödfokú valós együtthatós P(X) polinomokat, melyeknek a domináns együtthatójuk 1 és, ha a gyöke P-nek akkor 1-a illetve 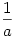 is gyöke P-nek. is gyöke P-nek.
|
|
| [2115] Lóczi Lajos | 2007-07-02 11:04:13 |
 A feladatban határozatlan integrálok szerepelnek: ha a két integrációs állandót különbözőnek választjuk, elég nehéznek tűnik a kérdés. Legyenek tehát egyenlőek.
Az egyenletet f-re rendezve látjuk, hogy f deriválható a pozitív és a negatív félegyenesen. Deriválva az egyenletet egy differenciálegyenletet kapunk, melynek megoldásai
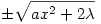
alakúak, valamely a 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen. 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen.
|
| Előzmény: [2113] Cckek, 2007-07-01 19:42:18 |
|
| [2114] Cckek | 2007-07-02 09:19:08 |
 Határozzuk meg az összes morfizmust (Q,+) és (Sn,o) között.
|
|
|
|
|
| [2110] Sirpi | 2007-06-22 23:50:30 |
 Na jó, akkor lecsapom :-)
Pont elolvastam a feladatot, majd a vihar miatt jött egy 2 órás áramszünet, azalatt volt időm (többek közt ezt is) végiggondolni.
Tehát f(f(n))=f(n)+n és f(1)=2.
A Fibonacci-számokon végigugrálva az embernek elég hamar előjön az a sejtése, hogy ![f(n) = [\frac{\sqrt 5+1}2 n + \frac 12]](keplet.cgi?k=50BD69C500659BDD) , vagyis a függvény lineáris , vagyis a függvény lineáris 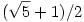 -es szorzóval, egészre kerekítve. -es szorzóval, egészre kerekítve.
És hogy ez miért jó? Legyen 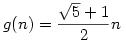 , vagyis a kerekítés nélküli függvény. Erre nyilván , vagyis a kerekítés nélküli függvény. Erre nyilván 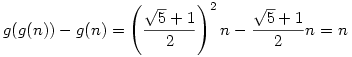
Másrészt minden n-re |f(n)-g(n)|<1/2, vagyis n-1<f(f(n))-f(n)<n+1, és mivel a különbség egész, ezért csak n lehet. Ezen kívül 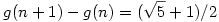 , vagyis , vagyis 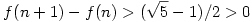 , így f(n+1)-f(n) , így f(n+1)-f(n) 1. 1.
|
| Előzmény: [2109] Cckek, 2007-06-22 19:38:21 |
|
| [2109] Cckek | 2007-06-22 19:38:21 |
 Felhívnám a tisztelt forumozók figyelmét, hogy a 2089-es hozzászolásomban kitűzött gyönyörűszép feladat még mindig megoldatlan:)
|
|
| [2108] Sirpi | 2007-06-21 11:50:54 |
 Szép elemzés!
Azért leírom azt is, hogy én mire jutottam. Talán kicsit egyszerűbb becsléseket használok, valamint semmilyen függvényvizsgálatra nincs szükség.
Legyen y:=n+x
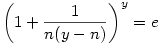
És itt, mikor 1/y-edik hatványra emelem mindkét oldalt:
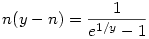
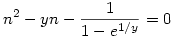
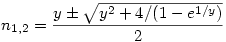
A két gyök közül az egyik lesz n, a másik xn. Az egyik gyök (a minuszos) 1 körül van, nézzük meg ezt alaposabban. Feltételezve, hogy y nagy, e1/y=1+1/y+1/(2y2)+O(1/y3), ahonnan
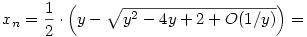
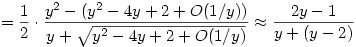
Ez pedig éppen az 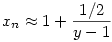 becslést adja, ahonnan szintén látszik az 1/2-es határérték. Viszont kihasználtam, hogy ha n becslést adja, ahonnan szintén látszik az 1/2-es határérték. Viszont kihasználtam, hogy ha n  , akkor y , akkor y  , ezt még annyival meg kell támogatni, hogy mivel a két gyök összege y, ezért valamelyik a kettő közül legalább y/2, válasszuk ezt n-nek, a másikat pedig xn-nek. , ezt még annyival meg kell támogatni, hogy mivel a két gyök összege y, ezért valamelyik a kettő közül legalább y/2, válasszuk ezt n-nek, a másikat pedig xn-nek.
* * *
Mindamellett azért is írtam le ezt az egészet, mert az az érdekes dolog látszik belőle, hogy ha nem n és xn lenne a feladatban, hanem x és f(x), akkor bejönne egy új gyök, hiszen az első lépésnél, a hatványozásnál az alap lehet épp negatív is, ha a kitevő (y) páros egész szám. Ekkor:
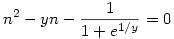
Ennek pedig egy pozitív (n), és egy negatív (xn) gyöke van. Viszont az sose fordulhat elő egyszerre, hogy y páros egész és n is egész, de ha n tetszőleges valós szám lehet, ami tart a végtelenbe, akkor valóban kapunk egy új gyököt:
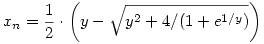
Itt most e1/y 1 triviális becslést alkalmazva 1 triviális becslést alkalmazva
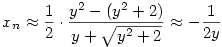
Szóval ha n nem feltétlen egész, akkor van egy másik (negatív) sorozat is xn-re (ilyenkor az alap -1 közelében van).
|
| Előzmény: [2106] Lóczi Lajos, 2007-06-21 03:16:23 |
|
|
| [2106] Lóczi Lajos | 2007-06-21 03:16:23 |
 Használjuk fel a pontosabb x-x2/2<ln (1+x)<x-x2/2+x3/3 egyenlőtlenséget. Ebből arra következtethetünk, hogy xn az
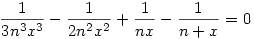
és az
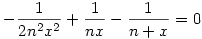
egyenletek (1-hez közeli) gyökei között van. Ez egy másod- és egy harmadfokú egyenlet, a megoldóképleteik felírhatók. Az ezekben szereplő négyzet- és köbgyököket a binomiális tétellel lehet sorbafejteni, amiből végül megkapjuk, hogy mind az alsó-, mind a felső becslése xn-nek 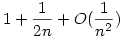 , ha n , ha n  . .
|
| Előzmény: [2104] Lóczi Lajos, 2007-06-21 01:34:29 |
|
|
| [2104] Lóczi Lajos | 2007-06-21 01:34:29 |
 A kérdéses xn sorozat az 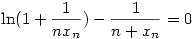 egyenlet gyöke. egyenlet gyöke.
Bizonyos mennyiségű számolással (első- és második deriváltak vizsgálata, határérték a 0-ban és a végtelenben, stb.) belátható, hogy ennek az egyenletnek minden, elég nagy n-re (pl. n>10) csak 1 gyöke van, az is 1 és pl. 2 között. Ez azért segít, mert ekkor használható az 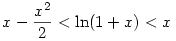 egyenlőtlenség (0<x<1). Így az eredeti egyenlet xn gyöke beszorítható két egyszerű egyenlet gyöke közé. Ebből kapjuk pl., hogy egyenlőtlenség (0<x<1). Így az eredeti egyenlet xn gyöke beszorítható két egyszerű egyenlet gyöke közé. Ebből kapjuk pl., hogy
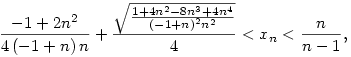
ami maga után vonja, hogy elég nagy n-ekre
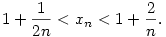
Tehát az (xn-1)na sorozatnak csak a=1 esetén lehet véges, nemnulla limesze (ha egyáltalán létezik).
Finomabb ötleteket fog igényelni annak kiderítése, hogy (xn-1)n melyik pozitív számhoz tart.
|
| Előzmény: [2103] Lóczi Lajos, 2007-06-19 22:38:34 |
|
|
|
|
|
|
| [2098] lorantfy | 2007-06-19 11:59:09 |
 Kedves Lajos!
Én úgy gondolkodtam, hogy az a és b megadásához minket az xn sorozat csak határértékben érdekel, vagyis nyugodtan helyettesíthető az 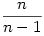 sorozattal, különben első egyenlet nem lenne igaz. sorozattal, különben első egyenlet nem lenne igaz.
Az 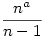 határértéke pedig a<1-nél 0, a=1-nél 1, a>1-nél végtelenbe megy. határértéke pedig a<1-nél 0, a=1-nél 1, a>1-nél végtelenbe megy.
|
| Előzmény: [2095] Lóczi Lajos, 2007-06-19 00:18:52 |
|
|
|
|





 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen.
0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen. (0,
(0, ) folytonos függvényeket melyekre:
) folytonos függvényeket melyekre:  >0
>0


 1 triviális becslést alkalmazva
1 triviális becslést alkalmazva  n úgy van definiálva, hogy
n úgy van definiálva, hogy 
