|
| [2131] HoA | 2007-07-03 11:24:07 |
 Igazad van. Sőt még abban is tévedtem, hogy x1,x2 tetszőleges multiplicitással szerepelhet. A valós együtthatós kikötés miatt ez nem igaz, csak párokban léphetnek fel.
Este végignéztem a hat gyök össszes párosításából adódó megoldásokat. Szerintem csak a már ismert 1/2, 2, -1, x1 és x2 értékeket kapjuk. Így aztán könnyen lehet, hogy csak az általad mondottakból adódó (x-x1)(x-x2)(x-1/2)(x-2)(x+1) polinom és a [2129] -beli P(x) a megoldás.
|
| Előzmény: [2130] Csimby, 2007-07-02 22:59:08 |
|
|
| [2129] HoA | 2007-07-02 16:53:25 |
 Szerintem nem kell túlbonyolítani. Odáig világos, hogy a 6 gyökhely 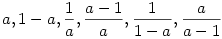 . Mivel a polinom csak ötödfokú, szükségképpen vannak köztük egyenlőek. Szépen végig kell nézni, mi adódik ha az egyes párokat egyenlővé tesszük. Például a = 1-a -ból a=1/2 és . Mivel a polinom csak ötödfokú, szükségképpen vannak köztük egyenlőek. Szépen végig kell nézni, mi adódik ha az egyes párokat egyenlővé tesszük. Például a = 1-a -ból a=1/2 és 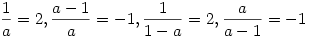 És itt nem baj, hogy további egybeeső gyökök vannak. A megoldás így írható: És itt nem baj, hogy további egybeeső gyökök vannak. A megoldás így írható: 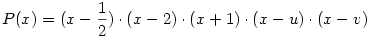 , ahol u és v egymástól függetlenül felveheti az 1/2, 2 és -1 értékeket. A további polinomokat a többi pár egyenlővé tételével keressük, és elhagyjuk az ismétléseket. Az , ahol u és v egymástól függetlenül felveheti az 1/2, 2 és -1 értékeket. A további polinomokat a többi pár egyenlővé tételével keressük, és elhagyjuk az ismétléseket. Az 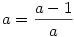 választással adódik a már szerepelt választással adódik a már szerepelt 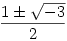 páros, ekkor valóban csak ez a két gyök van, jelöljük őket x1ésx2 vel, a polinom így P(x)=(x-x1).(x-x2).(x-u).(x-v).(x-z), ahol megintcsak u,v, és z x1vagyx2. És így tovább, ha van még... páros, ekkor valóban csak ez a két gyök van, jelöljük őket x1ésx2 vel, a polinom így P(x)=(x-x1).(x-x2).(x-u).(x-v).(x-z), ahol megintcsak u,v, és z x1vagyx2. És így tovább, ha van még...
|
| Előzmény: [2125] jonas, 2007-07-02 15:19:18 |
|
|
|
|
| [2125] jonas | 2007-07-02 15:19:18 |
 Egyébként a feladat azért trükkös, mert elindulhat valaki a rossz irányba is, hogy felteszi, hogy az öt gyök különönböző, és nem jut eszedbe, hogy 1-1/(1-1/(1-1/a))=a.
Ekkor gondolhat arra, hogy párba állítja a gyököket úgy, hogy a párja 1-a legyen, és mivel az öt páratlan, ezért biztosan gyök az 1/2 mert csak az párja önmagának, vagy hogy párba állítjuk a-t 1/a-val, és akkor biztosan gyök 1 és -1 közül az egyik.
Vagy arra is gondolhat (szintén ha az összes gyök különböző), hogy ha minden a gyökhöz 1-a is gyök, akkor a gyökök összege 5/2 így az x4 együtthatója -5/2, valamint hasonlóan a gyökök szorzata 1 így a konstans tag 1.
|
|
| [2124] jonas | 2007-07-02 15:11:54 |
 Na nézzük. Ha a=1-a, akkor a=1/2 és a gyökök 1/2,2,-1. Ha a=1/a akkor vagy a=-1 ami az előző eset, vagy a=1 jönne ki, de az nem jó, mert akkor az 1/0 is gyöke lenne a polinomnak.
Ha a=1/(1-a), akkor 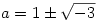 és ilyenkor csak két gyök van, mert a=1/(1-a)=(a-1)/a és 1-a=1/a=a/(a-1). és ilyenkor csak két gyök van, mert a=1/(1-a)=(a-1)/a és 1-a=1/a=a/(a-1).
Ezzel ki is merítettük az összes lehetőséget a gyökökre nézve, de a polinomokat nem adtuk meg.
|
| Előzmény: [2122] Csimby, 2007-07-02 13:53:58 |
|
|
|
|
|
|
| [2118] Csimby | 2007-07-02 13:37:44 |
 (reciprok képzés, 1-x, nem vezet ki közülük, viszont ezeknek mind szerepelnie kell) Kéne még vacakolni hogy mi van ha egybeesik pár. De úgy emlékszem algerba gyakorlaton volt valami hasonló Galois elmélet keretein belül. Majd ha végeztem a diffegy vizsgával és lesz időm megkeresem :-)
|
| Előzmény: [2117] Csimby, 2007-07-02 13:31:30 |
|
|
| [2116] Cckek | 2007-07-02 12:48:26 |
 Szép:) Amúgy ezek második fokozati vizsgakérdések itt Romániában. Itt van még egy ha érdekel valakit:
Határozzuk meg azokat az ötödfokú valós együtthatós P(X) polinomokat, melyeknek a domináns együtthatójuk 1 és, ha a gyöke P-nek akkor 1-a illetve 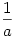 is gyöke P-nek. is gyöke P-nek.
|
|
| [2115] Lóczi Lajos | 2007-07-02 11:04:13 |
 A feladatban határozatlan integrálok szerepelnek: ha a két integrációs állandót különbözőnek választjuk, elég nehéznek tűnik a kérdés. Legyenek tehát egyenlőek.
Az egyenletet f-re rendezve látjuk, hogy f deriválható a pozitív és a negatív félegyenesen. Deriválva az egyenletet egy differenciálegyenletet kapunk, melynek megoldásai
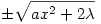
alakúak, valamely a 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen. 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen.
|
| Előzmény: [2113] Cckek, 2007-07-01 19:42:18 |
|
| [2114] Cckek | 2007-07-02 09:19:08 |
 Határozzuk meg az összes morfizmust (Q,+) és (Sn,o) között.
|
|
|
|
|
| [2110] Sirpi | 2007-06-22 23:50:30 |
 Na jó, akkor lecsapom :-)
Pont elolvastam a feladatot, majd a vihar miatt jött egy 2 órás áramszünet, azalatt volt időm (többek közt ezt is) végiggondolni.
Tehát f(f(n))=f(n)+n és f(1)=2.
A Fibonacci-számokon végigugrálva az embernek elég hamar előjön az a sejtése, hogy ![f(n) = [\frac{\sqrt 5+1}2 n + \frac 12]](keplet.cgi?k=50BD69C500659BDD) , vagyis a függvény lineáris , vagyis a függvény lineáris 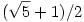 -es szorzóval, egészre kerekítve. -es szorzóval, egészre kerekítve.
És hogy ez miért jó? Legyen 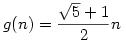 , vagyis a kerekítés nélküli függvény. Erre nyilván , vagyis a kerekítés nélküli függvény. Erre nyilván 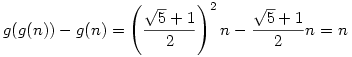
Másrészt minden n-re |f(n)-g(n)|<1/2, vagyis n-1<f(f(n))-f(n)<n+1, és mivel a különbség egész, ezért csak n lehet. Ezen kívül 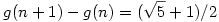 , vagyis , vagyis 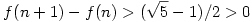 , így f(n+1)-f(n) , így f(n+1)-f(n) 1. 1.
|
| Előzmény: [2109] Cckek, 2007-06-22 19:38:21 |
|
| [2109] Cckek | 2007-06-22 19:38:21 |
 Felhívnám a tisztelt forumozók figyelmét, hogy a 2089-es hozzászolásomban kitűzött gyönyörűszép feladat még mindig megoldatlan:)
|
|
| [2108] Sirpi | 2007-06-21 11:50:54 |
 Szép elemzés!
Azért leírom azt is, hogy én mire jutottam. Talán kicsit egyszerűbb becsléseket használok, valamint semmilyen függvényvizsgálatra nincs szükség.
Legyen y:=n+x
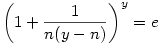
És itt, mikor 1/y-edik hatványra emelem mindkét oldalt:
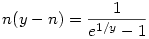
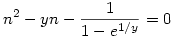
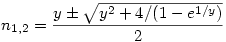
A két gyök közül az egyik lesz n, a másik xn. Az egyik gyök (a minuszos) 1 körül van, nézzük meg ezt alaposabban. Feltételezve, hogy y nagy, e1/y=1+1/y+1/(2y2)+O(1/y3), ahonnan
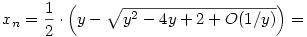
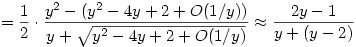
Ez pedig éppen az 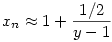 becslést adja, ahonnan szintén látszik az 1/2-es határérték. Viszont kihasználtam, hogy ha n becslést adja, ahonnan szintén látszik az 1/2-es határérték. Viszont kihasználtam, hogy ha n  , akkor y , akkor y  , ezt még annyival meg kell támogatni, hogy mivel a két gyök összege y, ezért valamelyik a kettő közül legalább y/2, válasszuk ezt n-nek, a másikat pedig xn-nek. , ezt még annyival meg kell támogatni, hogy mivel a két gyök összege y, ezért valamelyik a kettő közül legalább y/2, válasszuk ezt n-nek, a másikat pedig xn-nek.
* * *
Mindamellett azért is írtam le ezt az egészet, mert az az érdekes dolog látszik belőle, hogy ha nem n és xn lenne a feladatban, hanem x és f(x), akkor bejönne egy új gyök, hiszen az első lépésnél, a hatványozásnál az alap lehet épp negatív is, ha a kitevő (y) páros egész szám. Ekkor:
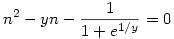
Ennek pedig egy pozitív (n), és egy negatív (xn) gyöke van. Viszont az sose fordulhat elő egyszerre, hogy y páros egész és n is egész, de ha n tetszőleges valós szám lehet, ami tart a végtelenbe, akkor valóban kapunk egy új gyököt:
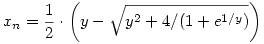
Itt most e1/y 1 triviális becslést alkalmazva 1 triviális becslést alkalmazva
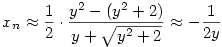
Szóval ha n nem feltétlen egész, akkor van egy másik (negatív) sorozat is xn-re (ilyenkor az alap -1 közelében van).
|
| Előzmény: [2106] Lóczi Lajos, 2007-06-21 03:16:23 |
|







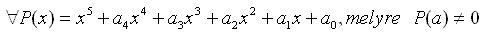

 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen.
0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen. (0,
(0, ) folytonos függvényeket melyekre:
) folytonos függvényeket melyekre:  >0
>0

 1 triviális becslést alkalmazva
1 triviális becslést alkalmazva