|
| [2156] Csimby | 2007-07-26 23:20:32 |
 Hát ez nagyon ügyes, gratulálok!
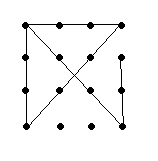
328.-ban az a feladat pl. n=4-re, hogy az ábrán látható 16 ponthoz megadható e egy 5 szakaszból álló töröttvonal amit a "ceruza felemelése nélkül" meg tudunk rajzolni és mind a 16 ponton átmegy. n=3-ra van ilyen 4-vonalból ez az ábráról leolvasható. Valaki azt állította egy ismerősömnek, hogy minden n-re van ilyen töröttvonal, de szerintem már n=4-re sincs. (pl. az ábrán 2 pont kimarad)
|
 |
| Előzmény: [2154] nadorp, 2007-07-26 21:08:23 |
|
|
| [2154] nadorp | 2007-07-26 21:08:23 |
 Másképp számoltam, a módszert még egyetemen hallottam egy szenzációs tanáromtól. Legyen 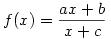 és tekintsük f(x) fixpontjait, azaz az f(x)=x egyenletet, x2+(c-a)x-b=0. Ha ennek két ( akár komplex) gyöke x1,x2, akkor és tekintsük f(x) fixpontjait, azaz az f(x)=x egyenletet, x2+(c-a)x-b=0. Ha ennek két ( akár komplex) gyöke x1,x2, akkor
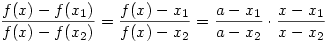 ( legyen ez a 327/a/a feladat :-), valamint ( legyen ez a 327/a/a feladat :-), valamint
x1+x2=a-c és x1x2=-b
Indukcióval azonnal adódik, hogy 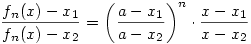 . .
Ha most a,x1,x2 értékét úgy választjuk meg, hogy
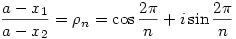 ( az első primitív n-dik egységgyök), akkor fn(x)=x adódik. Ha még x1=x2konjugált ( nem tudom a felső vízszintes vonalat TeX-ben :-), akkor x1,x2 lehetnek egy másodfokú egyenlet komplex gyökei. ( az első primitív n-dik egységgyök), akkor fn(x)=x adódik. Ha még x1=x2konjugált ( nem tudom a felső vízszintes vonalat TeX-ben :-), akkor x1,x2 lehetnek egy másodfokú egyenlet komplex gyökei.
Könnyen látható, hogy a=1, x1=- n , x2=- n , x2=- n-1 jók lesznek, innen b és c értéke a fentiek alapján könnyen számolható. n-1 jók lesznek, innen b és c értéke a fentiek alapján könnyen számolható.
|
| Előzmény: [2153] Csimby, 2007-07-26 19:17:17 |
|
| [2153] Csimby | 2007-07-26 19:17:17 |
 Köszi! Hogyha a törtfüggvénybe n-szer behelyettesítem önmagát, majd egyenlővé teszem ezt x-vel. a=1, b=-1-et helyettesítek és egyoldalra rendezem, akkor ebből kiemelhető lesz c-egy polinomja, amit megoldok hogy mikor 0. Így jön ki c-re az amit a megoldásban írtál? (n=3-ra ez működik, de 4-re nem szenvedtem végig)
Más: 328.-ra szerintem nemleges a válasz.
|
| Előzmény: [2152] nadorp, 2007-07-26 12:03:32 |
|
|
|
| [2150] nadorp | 2007-07-26 10:02:25 |
 A 327/a feladatra szerintem pozitív a válasz, azaz minden n-re van olyan elsőfokú racionális törtfüggvény ( 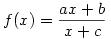 alakú), melyre f(n)=x ( ez most kompozíció és nem deriválás :-) alakú), melyre f(n)=x ( ez most kompozíció és nem deriválás :-)
|
| Előzmény: [2148] Csimby, 2007-07-25 18:03:01 |
|
|
| [2148] Csimby | 2007-07-25 18:03:01 |
 Előző feladatomra sajnos senki se reagált :-( Itt van pár új.
328.feladat A [2].hozzászólásban szereplő 2.feladat általánosítható-e n×n-es négyzetre és n+1 egymáshoz csatlakozó szakaszra. Már n=4-re is kíváncsi lennék hogy mit mondtok.
329.feladat Két Sudoku -táblázat távolsága legyen azon mezők száma ahol eltérnek egymástól. Milyen távolságok fordulhatnak elő két táblázat között.
Érdekes kérdés még hogy hány különböző Sudoku-táblázat van, illetve, hogy legkevesebb hány mezőt lehet úgy megadni, hogy legyen egyértelmű megoldás. De ezekről sajnos azt találtam hogy igen nehezek lehetnek.
|
|
|
| [2146] Lajos Arpad | 2007-07-21 10:41:18 |
 328. feladat Vegyük a kôvetkezô mértani haladványt: 1, x, x*x... x természetes szám és nagyobb mint 1, n természetes sám S(n)=1+x+...+(x) az n-dik hatványon Bizonyítsuk be, hogy: S(n)/(x-1) természetes szám <=> (n+1)/(x-1) természetes szám.
|
|
|
|
|
| [2142] Cckek | 2007-07-17 22:37:13 |
 A nagy meleg miatt, megaztán nyaralás okán elég hulla a forum, itt van egy frissitő:
|
|
| [2141] Csimby | 2007-07-07 04:02:03 |
 327.feladat Az f:R R fv. n-edik hatványa legyen fn=fo...of - n db f összekomponálva (tegyük fel, hogy Rfk R fv. n-edik hatványa legyen fn=fo...of - n db f összekomponálva (tegyük fel, hogy Rfk Dfk+1, k Dfk+1, k 1 vagy k 1 vagy k 0 - ez esetben f0:=id, még nem tudom hogy lesz érdekesebb a feladat 0-val vagy 1-gyel. Megj.: Ha k 0 - ez esetben f0:=id, még nem tudom hogy lesz érdekesebb a feladat 0-val vagy 1-gyel. Megj.: Ha k 0 akkor f az egész R-en értelmezett és így fn=id-ből következik, hogy f összes hatványa is egész R-en értelmezett). Egy f R 0 akkor f az egész R-en értelmezett és így fn=id-ből következik, hogy f összes hatványa is egész R-en értelmezett). Egy f R R fv. rendje legyen az a legkisebb n pozitív egész, melyre fn=id. R fv. rendje legyen az a legkisebb n pozitív egész, melyre fn=id.
a. feladat Keressünk minden n-re n-rendű f:R R függvényt. R függvényt.
A Cckek által [2116]-ban kitűzött feladatban pl. az 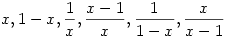 függvények az R-{0,1} értelmezési tartományban csoportot alkotnak a kompozícióra nézve az R függvények az R-{0,1} értelmezési tartományban csoportot alkotnak a kompozícióra nézve az R R fv.-ek terében. Ebben a csoportban R fv.-ek terében. Ebben a csoportban 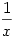 rendje 2, rendje 2, 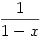 rendje 3, a csoport 6 elemű, így ez a csoport izomorf S3-mal. rendje 3, a csoport 6 elemű, így ez a csoport izomorf S3-mal.
b. feladat Mely G csoportoknak adható meg ilyen R R fv.-ekkel reprezentációja? (keressünk ilyen reprezentációkat) Megj.: Az a. feladat tehát azt kéri, hogy adjuk meg minden n-re Zn egy reprezentációját és n=2,3-ra már mutattunk példát, igaz egyik sem volt az egész R-en értelmezve, kérdés: van-e ilyen?. R fv.-ekkel reprezentációja? (keressünk ilyen reprezentációkat) Megj.: Az a. feladat tehát azt kéri, hogy adjuk meg minden n-re Zn egy reprezentációját és n=2,3-ra már mutattunk példát, igaz egyik sem volt az egész R-en értelmezve, kérdés: van-e ilyen?.
u.i.: Most egy hétig nem leszek, pedig kíváncsi vagyok miket fogtok írni, mindenesetre még én sem gondolkoztam a feladatokon, csak a [2116]-ban kitűzött feladat kapcsán vetődtek fel bennem ezek a kérdések.
|
|
|
|
| [2138] Csimby | 2007-07-05 17:33:57 |
 Szia!
2/A-ban card a számosságot jelenti? És ha igen, akkor abból hogy ez alef0 miért következik, hogy Z? (Pl. Q nem izomorf Z-vel hiszen nem ciklikus)
|
| Előzmény: [2137] Cckek, 2007-07-05 10:42:17 |
|
| [2137] Cckek | 2007-07-05 10:42:17 |
 Természetesen ki kell zárni a G={0} esetet. Először bebizonyítjuk, hogy G nem korlátos. Legyen
g G,g G,g 0.Mivel G csoport,(g 0.Mivel G csoport,(g G G -g -g G) vehetjük g>0 és ng G) vehetjük g>0 és ng G minden n G minden n N esetén. Ekkor az arkhimédészi axioma értelmében minden r N esetén. Ekkor az arkhimédészi axioma értelmében minden r R-re van olyan n R-re van olyan n N melyre ng>r. Tehát G nem korlátos, és G nem véges. N melyre ng>r. Tehát G nem korlátos, és G nem véges.
1. Ha G-nek nincs torlodási pontja mivel G zárt és nem korlátos, ugyanakkor nG G igy G megszámlálható végtelen sok izolált pontból áll, tehát izomorf Z-vel. G igy G megszámlálható végtelen sok izolált pontból áll, tehát izomorf Z-vel.
2. Ha x G torlodási pontja G-nek, akkor ha V környezete x-nek,(V végtelen sok pontot tartalmaz a G-ből)akkor minden y G torlodási pontja G-nek, akkor ha V környezete x-nek,(V végtelen sok pontot tartalmaz a G-ből)akkor minden y G esetén (y-x)+V környezete y-nak (és végtelen sok pontot tartalmaz a G-ből), tehát y szintén torlodási pont. Tehát ebben az esetben G minden pontja torlodási pont. Két lehetségünk van: G esetén (y-x)+V környezete y-nak (és végtelen sok pontot tartalmaz a G-ből), tehát y szintén torlodási pont. Tehát ebben az esetben G minden pontja torlodási pont. Két lehetségünk van:
A. G egyetlen pontjának sincs G-beli környezete. Ekkor G minden pontjának a környezetei megszámlálható végtelen sok pontot tartalmaznak G-ből, tehát cardG= 0 igy izomorf Z vel. 0 igy izomorf Z vel.
B. Létezik x G úgy, hogy V=(x- G úgy, hogy V=(x- ,x+ ,x+ ) ) G. Ekkor V-x=(- G. Ekkor V-x=(- , , ) ) G és az archimédészi axioma értelmében G és az archimédészi axioma értelmében
(-n ,n ,n ) ) G, G, n n N tehát G=R N tehát G=R
|
| Előzmény: [2133] Csimby, 2007-07-03 16:56:32 |
|
|
|
|
|







 n , x2=-
n , x2=- 3 esetén
3 esetén 
 n=k(x-1)-1 tehát
n=k(x-1)-1 tehát  R fv. n-edik hatványa legyen fn=fo...of - n db f összekomponálva (tegyük fel, hogy Rfk
R fv. n-edik hatványa legyen fn=fo...of - n db f összekomponálva (tegyük fel, hogy Rfk Dfk+1, k
Dfk+1, k =inf{|g|,g
=inf{|g|,g G-{0}}.
G-{0}}. 0.Mivel G csoport,(g
0.Mivel G csoport,(g 0 igy izomorf Z vel.
0 igy izomorf Z vel.  ,x+
,x+ n
n