|
| [2168] Csimby | 2007-07-28 00:08:50 |
 Szia! Köszi az ábrákat! Az én algoritmusom most veszem észre, hogy mégsem jó, mert noha megfelelő számú szakaszból áll, az egyiket 2 részletben húzom be az pedig csalás (1 behúzással nem lehet mert van benne egy 3-fokú csúcs így muszáj abból indulni). Amúgy azt akartam, hogy az n=5-re talált "nem kilépő" megoldásomat (amit még nem akarok lerajzolni) L-alakban két szakasszal kibővítem és egy régi szakaszt meghosszabítok, ekkor n=6 egy megoldását kapom és ez folytatható is lenne, csak hát mégsem jó.
|
| Előzmény: [2167] epsilon, 2007-07-27 18:13:42 |
|
| [2167] epsilon | 2007-07-27 18:13:42 |
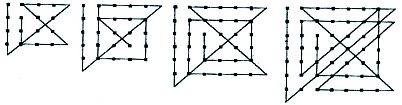
 A 328-as feladat kapcsán a következő biztos: n×n pont összeköthető 2n-2 szakaszból álló töröttvonallal, a kért feltétellel. Szemléltetés és algoritmus kialakítása végett itt egy "kép" egy pár esettel:
|
 |
| Előzmény: [2156] Csimby, 2007-07-26 23:20:32 |
|
| [2166] Hajba Károly | 2007-07-27 12:47:46 |
 A spirál alatt azt értem, hogy a mátrixot kivülröl körkörösen, majd mindig befelé haladva folyamatosan felfűztem. Ehhez, amint jól látod 1-gyel több vonal kell. Anno így határoztam meg a szükséges lépésszámot, azaz a spirálban található vonalak számából elvettem egyet. Persze később a képletet is meghatároztam. :o)
---
Az n=5 nemkilépő és visszazárón akkor elkezdek gondolkodni.
|
| Előzmény: [2164] Csimby, 2007-07-27 09:52:47 |
|
|
| [2164] Csimby | 2007-07-27 09:52:47 |
 Most látom csak hogy ez a feladat egyszer mennyire ki lett már vesézve (pl. 39.feladat), Spirálozás alatt amúgy azt érted hogy mindig az egyel kisebb oldalhosszú négyzet megoldásából állítjuk elő a következőt? Vagy mire gondolsz? Mert ugye ha csak úgy felspirálozzuk a pontokat, akkor az 1-gyel több szakasz.
|
| Előzmény: [2162] Hajba Károly, 2007-07-27 08:33:24 |
|
|
| [2162] Hajba Károly | 2007-07-27 08:33:24 |
 A "spirálozást" még anno eljátszottam, mikor a 7*7-es megoldását kerestem. E témakörben az lehet még érdekes, hogy melyik legkisebb n-nél lehet már megoldást találni, (1)hogy vissza lehessen zárni, (2)hogy ne lépjen ki a törtvonal a külső pontokon ill. (1) és (2) egyszerre. n=4-re már lehet zárt görgét találni, n=5-re pedig nem kilépőt. A kettő együtt eddig még az ismert n=7.
|
| Előzmény: [2161] Csimby, 2007-07-27 01:31:34 |
|
|
|
| [2159] Hajba Károly | 2007-07-27 00:54:05 |
 Szerintem az általánosító képlet 2(n-1), azaz a mátrix pontjait spirálisan 2(n-1)+1 szakaszból álló törtvonal segítségével tudjuk felfűzni.
S így ezen feltételekkel szerintem már megoldhatóak. Lásd n=7 esetében már két szigorításal is. (nincs kilépés és visszazár)
|
| Előzmény: [2148] Csimby, 2007-07-25 18:03:01 |
|
|
|
| [2156] Csimby | 2007-07-26 23:20:32 |
 Hát ez nagyon ügyes, gratulálok!
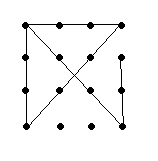
328.-ban az a feladat pl. n=4-re, hogy az ábrán látható 16 ponthoz megadható e egy 5 szakaszból álló töröttvonal amit a "ceruza felemelése nélkül" meg tudunk rajzolni és mind a 16 ponton átmegy. n=3-ra van ilyen 4-vonalból ez az ábráról leolvasható. Valaki azt állította egy ismerősömnek, hogy minden n-re van ilyen töröttvonal, de szerintem már n=4-re sincs. (pl. az ábrán 2 pont kimarad)
|
 |
| Előzmény: [2154] nadorp, 2007-07-26 21:08:23 |
|
|
| [2154] nadorp | 2007-07-26 21:08:23 |
 Másképp számoltam, a módszert még egyetemen hallottam egy szenzációs tanáromtól. Legyen 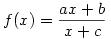 és tekintsük f(x) fixpontjait, azaz az f(x)=x egyenletet, x2+(c-a)x-b=0. Ha ennek két ( akár komplex) gyöke x1,x2, akkor és tekintsük f(x) fixpontjait, azaz az f(x)=x egyenletet, x2+(c-a)x-b=0. Ha ennek két ( akár komplex) gyöke x1,x2, akkor
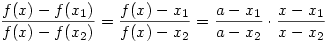 ( legyen ez a 327/a/a feladat :-), valamint ( legyen ez a 327/a/a feladat :-), valamint
x1+x2=a-c és x1x2=-b
Indukcióval azonnal adódik, hogy 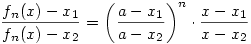 . .
Ha most a,x1,x2 értékét úgy választjuk meg, hogy
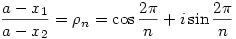 ( az első primitív n-dik egységgyök), akkor fn(x)=x adódik. Ha még x1=x2konjugált ( nem tudom a felső vízszintes vonalat TeX-ben :-), akkor x1,x2 lehetnek egy másodfokú egyenlet komplex gyökei. ( az első primitív n-dik egységgyök), akkor fn(x)=x adódik. Ha még x1=x2konjugált ( nem tudom a felső vízszintes vonalat TeX-ben :-), akkor x1,x2 lehetnek egy másodfokú egyenlet komplex gyökei.
Könnyen látható, hogy a=1, x1=- n , x2=- n , x2=- n-1 jók lesznek, innen b és c értéke a fentiek alapján könnyen számolható. n-1 jók lesznek, innen b és c értéke a fentiek alapján könnyen számolható.
|
| Előzmény: [2153] Csimby, 2007-07-26 19:17:17 |
|
| [2153] Csimby | 2007-07-26 19:17:17 |
 Köszi! Hogyha a törtfüggvénybe n-szer behelyettesítem önmagát, majd egyenlővé teszem ezt x-vel. a=1, b=-1-et helyettesítek és egyoldalra rendezem, akkor ebből kiemelhető lesz c-egy polinomja, amit megoldok hogy mikor 0. Így jön ki c-re az amit a megoldásban írtál? (n=3-ra ez működik, de 4-re nem szenvedtem végig)
Más: 328.-ra szerintem nemleges a válasz.
|
| Előzmény: [2152] nadorp, 2007-07-26 12:03:32 |
|
|
|
| [2150] nadorp | 2007-07-26 10:02:25 |
 A 327/a feladatra szerintem pozitív a válasz, azaz minden n-re van olyan elsőfokú racionális törtfüggvény ( 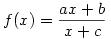 alakú), melyre f(n)=x ( ez most kompozíció és nem deriválás :-) alakú), melyre f(n)=x ( ez most kompozíció és nem deriválás :-)
|
| Előzmény: [2148] Csimby, 2007-07-25 18:03:01 |
|
|
| [2148] Csimby | 2007-07-25 18:03:01 |
 Előző feladatomra sajnos senki se reagált :-( Itt van pár új.
328.feladat A [2].hozzászólásban szereplő 2.feladat általánosítható-e n×n-es négyzetre és n+1 egymáshoz csatlakozó szakaszra. Már n=4-re is kíváncsi lennék hogy mit mondtok.
329.feladat Két Sudoku -táblázat távolsága legyen azon mezők száma ahol eltérnek egymástól. Milyen távolságok fordulhatnak elő két táblázat között.
Érdekes kérdés még hogy hány különböző Sudoku-táblázat van, illetve, hogy legkevesebb hány mezőt lehet úgy megadni, hogy legyen egyértelmű megoldás. De ezekről sajnos azt találtam hogy igen nehezek lehetnek.
|
|
|
| [2146] Lajos Arpad | 2007-07-21 10:41:18 |
 328. feladat Vegyük a kôvetkezô mértani haladványt: 1, x, x*x... x természetes szám és nagyobb mint 1, n természetes sám S(n)=1+x+...+(x) az n-dik hatványon Bizonyítsuk be, hogy: S(n)/(x-1) természetes szám <=> (n+1)/(x-1) természetes szám.
|
|
|










 n , x2=-
n , x2=- 3 esetén
3 esetén 
 n=k(x-1)-1 tehát
n=k(x-1)-1 tehát