| [2294] Yegreg | 2007-09-18 19:29:55 |
 Igen, szép megoldás, nekem is ez adódott. A kérdés egyébként úgy is lefordítható, hogy "mennyire lehet nem egyenlőszárú egy háromszög?", ebből már sejthető, hogy miért is vetődött fel bennem a feladat. :)
|
|
| [2293] SmallPotato | 2007-09-18 19:27:16 |
 Tulképpen nem véletlen, hogy az aranymetszés aránya jön ki: tegyük fel, hogy a háromszög c=a+b jelleggel elfajul; ekkor ha a c oldalt a C csúcs az aranymetszés szerint osztja, akkor per definitionem 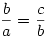 ; ellenkező esetben valamelyik arány a ; ellenkező esetben valamelyik arány a 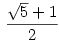 -nél kisebb, a másik pedig nagyobb. -nél kisebb, a másik pedig nagyobb.
(Ez a "levezetés" természetesen nem tartalmazza a nem-elfajult esetet.)
|
| Előzmény: [2292] SmallPotato, 2007-09-18 19:13:33 |
|
| [2292] SmallPotato | 2007-09-18 19:13:33 |
 Legyen mondjuk a b b c. Ekkor a három, érdemben vizsgálandó, egynél nem kisebb hányados c. Ekkor a három, érdemben vizsgálandó, egynél nem kisebb hányados 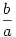 , , 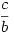 és és 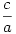 . Ezek közül (a kiinduló reláció értelmében) . Ezek közül (a kiinduló reláció értelmében) 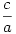 nem lehet a legkisebb; marad tehát nem lehet a legkisebb; marad tehát 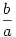 (legyen ez p; ekkor b=ap) és (legyen ez p; ekkor b=ap) és 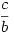 (legyen ez q; ekkor c=bq). Értelemszerűen p (legyen ez q; ekkor c=bq). Értelemszerűen p 1 és q 1 és q 1. 1.
A háromszög oldalaira vonatkozó egyenlőtlenség értelmében c<a+b. Ebbe helyettesítsük be b=ap és c=bq=apq értékét; kapjuk
apq<a+ap
Innen a-val osztva (mivel a>0, az osztás elvégezhető és az egyenlőtlenség iránya is változatlan):
pq<1+p
Innen p-vel osztva (p>0 miatt az osztás elvégezhető és az egyenlőtlenség iránya is változatlan):
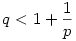
Tekintve, hogy p 1, kapjuk, hogy q<2. Ha azonban q "2-höz közeli" érték, akkor láthatóan p-nek "1-hez közelinek" kell lennie, tehát ilyenkor p a kisebb. p növelésével egy ponton p és q egyenlővé válik; ez a pont (az egyenlőtlenséget egyenlőségként megoldva pl p-re) 1, kapjuk, hogy q<2. Ha azonban q "2-höz közeli" érték, akkor láthatóan p-nek "1-hez közelinek" kell lennie, tehát ilyenkor p a kisebb. p növelésével egy ponton p és q egyenlővé válik; ez a pont (az egyenlőtlenséget egyenlőségként megoldva pl p-re)
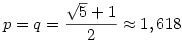
. Ha p ennél nagyobb, akkor q (ennél és így p-nél is) kisebb.
p és q közül a kisebbik tehát az 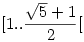 jobbról nyílt intervallumba kell hogy essen. (ha "nem nagyobbik" lett volna a kérdés, akkor az intervallum jobbról is zárt lenne.) jobbról nyílt intervallumba kell hogy essen. (ha "nem nagyobbik" lett volna a kérdés, akkor az intervallum jobbról is zárt lenne.)
|
| Előzmény: [2290] Yegreg, 2007-09-18 17:18:57 |
|
| [2291] Sirpi | 2007-09-18 17:27:20 |
 Köszi. Mindezt csak Jónás gépének védelmében tettem :-)
Egyébként még annyi kiegészítés az a) részhez, hogy tovább lehet csökkenteni a vizsgálatok számát, ugyanis
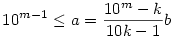
Innen azt kapjuk, hogy 10b>10k-1-nek teljesülnie kell, vagyis b k. így elég 36 esetet megnézni. k. így elég 36 esetet megnézni.
Tehát ha pl. k=9, akkor b=9, vagyis a=9.(10m-9)/89, és a legkisebb m, amire ez egész, az m=43, ahonnan rögtön kapunk egy elvileg nem periodikus 44 jegyű megoldást. Hasonlóan k=8-ra m=12.
k=7-re a nevező 69, vagyis 3.23. m=21-re a számláló osztható 69-cel (nincs kisebb, ami osztható lenne 23-mal), ebből is kapunk egy megoldást.
Hasonlóan végig lehetne nézni az összes k-t, csak nekem ehhez nincs sok türelmem :-)
* * *
Azért pár példa, amit kiszámoltam:
91011235955056179775280898876404494382022471 / 10112359550561797752808988764044943820224719 = 9
8101265822784 / 1012658227848 = 8 (ez pont 13 jegyű :-) )
210526315789473684 / 105263157894736842 = 2
2 és 9 között minden arányra van megoldás.
|
| Előzmény: [2289] Lóczi Lajos, 2007-09-18 12:40:43 |
|
| [2290] Yegreg | 2007-09-18 17:18:57 |
 Legyen a,b,c egy háromszög oldalainak hossza. Vegyük az a/b, b/a, b/c, c/b, c/a, a/c számok közül az 1-nél nem kisebbeket, és legyen ezek közül x a legkisebb. Milyen nagy lehet x?
|
|
|
| [2288] Sirpi | 2007-09-18 10:00:38 |
 Ugyanúgy intézhető el az a) eset, ekkor
k(10a+b)=10mb+a
ahonnan
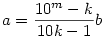
Rögzített m-re tehát elég végignézni a b=1,2,...,9, k=2,3,...,9 eseteket, ami összesen 72 db. ellenőrzést jelent (ez pl. m+1=13-ra, amit épp vizsgálsz, Jónás, elég messze van a 2 naptól, még akár kézzel is ;-) ).
Nyilván lehet további egyszerűsítéseket tenni, pl. k=3-ra a 10m-3-nak oszthatónak kell lennie 29-cel, ami csak akkor teljesülhet, ha m+1 osztható 28-cal (és ilyenkor b=3,4,5,6,7,8,9 mind megoldást ad, b=1,2 még túl kicsi).
És az is látszik ebből a felírásból, hogy miért jöttek ki ezek a furának ható törtek, pl. az 1/13. Ha k=4, akkor a=99...96/39.b=33...32/13.b, és már meg is jelent a 13-as nevező (és a számlálóból a -k-t elhanyagolva kapjuk, hogy 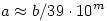 ). ).
Egyébként m=5-re (vagyis a 6-jegyű n-ekre) a következő megoldások adódtak:
230769 923076 (k=4,b=9) 923076 (k=4,b=9)
205128 820512 (k=4,b=8) 820512 (k=4,b=8)
179487 717948 (k=4,b=7) 717948 (k=4,b=7)
153846 615384 (k=4,b=6) 615384 (k=4,b=6)
128205 512820 (k=4,b=5) 512820 (k=4,b=5)
102564 410256 (k=4,b=4) 410256 (k=4,b=4)
142857 714285 (k=5,b=7) 714285 (k=5,b=7)
Más k-ra nem adódik megoldás. Innentől lehet progit írni, hogy a többi m-re is végignézzük a lehetőségeket, de szerintem az is járható út, hogy végignézzük a k=2,3,...,9 eseteket, és mindegyikre megnézzük, hogy mely m-ekre ad megoldást. Nagyon úgy néz ki, hogy ha két megoldást azonosnak tekintünk akkor, ha ugyanannak a blokknak a többször egymás után írásával adódnak, akkor csak véges sok megoldás van összesen.
|
| Előzmény: [2287] Sirpi, 2007-09-18 09:38:06 |
|
| [2287] Sirpi | 2007-09-18 09:38:06 |
 Mielőtt leégne a nagy munkától a procid, próbáljuk meg "kicsit" szűkíteni a keresési teret.
Nézzük először a b) esetet, ott program nélkül is sikerült felderítenem az összes megoldást. Legyen a vizsgálandó n szám m+1-jegyű (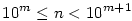 ), és írjuk fel n=10a+b alakban, ahol 1 ), és írjuk fel n=10a+b alakban, ahol 1 b b 9, és 10m-1 9, és 10m-1 a<10m, tehát az első m jegyből alkotott számot jelöli a, az utolsót pedig b. Vigyük b-t előre (az így kapott szám 10mb+a), és tegyük fel, hogy ettől a szám k-adrészére változik (mivel mindkét szám m+1 jegyű, és valódi osztót keresünk, ezért 2 a<10m, tehát az első m jegyből alkotott számot jelöli a, az utolsót pedig b. Vigyük b-t előre (az így kapott szám 10mb+a), és tegyük fel, hogy ettől a szám k-adrészére változik (mivel mindkét szám m+1 jegyű, és valódi osztót keresünk, ezért 2 k k 9): 9):
10a+b=k(10mb+a)
Innen
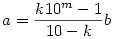
Az első észrevétel, hogy ha k>5, akkor a jobb oldal több, mint m-jegyű, hiszen legalább 5.10m-t osztjuk legfeljebb 4-gyel, amit még b-vel meg is szorzunk, ez már b=1 esetén is nagy.
Ha k=5, akkor a=499...9/5.b, viszont ekkor b csak 5 lehet, hogy egész számot kapjunk, megint nagy lesz a (499...9).
k=4 esetén a=399...9/6.b, itt b-t legalább 2-nek kell választanunk, hogy egész számot kapjunk, de b=2 esetén a=133...3, ami szintén sok. A k=3 esetet a végére hagyom, mert az az érdekes. k=2-re a=199...9/8.b, itt b csak 8 lehet, ekkor a=199...9, szintén túlcsordul.
Ha k=3, akkor a=299...9/7.b, ha b=7 lenne, akkor túl nagy számot kapnánk, ezért a 299...9 számnak oszthatónak kell lennie 7-tel. A 10m 7-es maradékai rendre (0-tól kezdve) 1, 3, 2, 6, 4, 5, és innentől ismétlődik, ezt 3-mal szorozva, majd 1-et kivonva a 2, 1, 5, 3, 4, 0 periódusú sorozatot kapjuk.
Az jött ki tehát, hogy csak akkor van megoldás, ha m+1 osztható 6-tal, és ilyenkor hogy elkerüljük a túlcsordulást, b csak 1 vagy 2 lehet.
Ekkor a következő megoldások adódnak:
428571 142857 (b=1) 142857 (b=1)
857142 285714 (b=2) 285714 (b=2)
428571428571 142857142857 (b=1) 142857142857 (b=1)
857142857142 285714285714 (b=2) 285714285714 (b=2)
stb.
Tehát a két alapmegoldás (amit a 3/7 és a 6/7 tizedestört alapjából kapunk) néhányszor egymás mögé írásával adódik az összes megoldás.
|
| Előzmény: [2286] jonas, 2007-09-17 22:34:43 |
|
| [2286] jonas | 2007-09-17 22:34:43 |
 Ellenőriztem, valóban csak az a kilenc darab 12 jegyű megoldás van, amit a hétjegyűek ismétléseként kapunk. Elindítom a programot 13 jegyűre, elvileg két nap alatt végeznie kell.
|
|
| [2285] jonas | 2007-09-17 16:31:36 |
 Hát, engem például meglep, hogy a 17 nem szerepel, holott az 1/17 tizedes törtként 16 periódusú.
Természetesen az ilyen sorozatoknak a Sloane-ben érdemes utánanézni. Az (a) feladat megoldásait A034089 adja meg, de meglepő módon a (b) nincs benne.
|
| Előzmény: [2282] Lóczi Lajos, 2007-09-17 15:46:43 |
|
|
| [2283] Lóczi Lajos | 2007-09-17 15:48:45 |
 Csak írd fel részletesen, mely azonosságoknak kell egy gyűrűben teljesülniük (modellként vedd a számokat az összeadással és a szorzással, csak a szorzás ne legyen kommutatív) -- és mindegyik automatikusan teljesülni fog, mert a leképezések között az összeadás és a kompozíció úgy van definiálva, hogy ezek pont teljesüljenek...
|
| Előzmény: [2278] diakmatekos, 2007-09-17 13:55:04 |
|
|
| [2281] jonas | 2007-09-17 15:16:49 |
 Tizenegyjegyű sincs. Lehet, hogy majd lefuttatom a kimerítő keresést a tizenkétjegyűekre is, mert az egy napon belül biztosan végezne. Eddig tizenkétjegyűekből csak a hatjegyűek ismétlését ismerem, tizenháromjegyűből pedig a következőket: 1012658227848 és 1139240506329 (az 1/79 jegyei), valamint 102564102564.
|
| Előzmény: [2279] jonas, 2007-09-17 13:57:56 |
|
| [2280] jonas | 2007-09-17 14:34:10 |
 Sőt, könnyen lehet, hogy sok másik példa is így áll elő, például 153846 az 1/13 jegyeiből; 102564 (a legkisebb ilyen szám) az 1/45-ből. Valójában az 1/7, 1/13, és 1/45 együtt magyarázatot adnak minden hatjegyű példa eredetére.
Érdekes feladat ez.
|
| Előzmény: [2275] Sirpi, 2007-09-17 13:07:29 |
|
|
| [2278] diakmatekos | 2007-09-17 13:55:04 |
 Sziasztok! Itt egy érdekes, (talán inkább nehéz) feladat:
Legyen U vektortér az F test fölött, és jelölje End(U) összes lineáris transzformációi halmazát. Igazolnunk kellene, hogy End((U),+,*) gyűrű, ahol a két művelet a lineáris leképezések ismert összeadása és a leképezésszorzás.
a hozzákezdéshez kellene vmi ötlet. Remélem tudtok segíteni. köszi
|
|
|
| [2276] jonas | 2007-09-17 13:26:26 |
 Meglepő módon, noha hatjegyű példából (a) 7 (b) 2 is van, nemhogy ennél kisebb nincs, de hét- és nyolcjegyű szám sincs, ami teljesíti a feltételek valamelyikét.
|
| Előzmény: [2273] jonas, 2007-09-17 13:00:51 |
|
|
|
| [2273] jonas | 2007-09-17 13:00:51 |
 Tévedtem, mégis van ilyen szám. Korábban vagy nem jól kerestem, vagy csak túl kicsi számok között. A legkisebb ilyen szám az (a) esetben 102564, mivel 4.102564=410256, a (b) esetben pedig 428571, mivel 428571=3.142857. Az utóbbira rá is kellett volna jönnöm, hiszen mindenki tudja, hogy ezek az ismétlődő jegyek az 1/7,2/7,...,6/7 törtekben. Ezeken kívül más ilyen számok is vannak.
|
| Előzmény: [2272] jonas, 2007-09-17 12:37:15 |
|
|
| [2271] Lóczi Lajos | 2007-09-16 19:53:51 |
 Van-e olyan n pozitív egész, hogy n
a.) valódi osztója J(n)-nek?
b.) valódi többszöröse J(n)-nek?
(A feladatban J(n) azt a pozitív egészt jelöli, amely n-ből úgy keletkezik, hogy annak utolsó számjegyét az első helyre mozgatjuk át. Nullával nem kezdődnek számok.)
|
|
| [2270] Sirpi | 2007-09-13 09:53:56 |
 Igen, ezt már én is végiggondoltam, és szerintem a kérdés úgy értelmes, hogy a sorrendet Te állíthatod fel, és az egymás utániaknak kell azonos távolságra lenniük. Egyébként nem teljesen világos, hogy miért kell ehhez térbe kimenni, ugyanis, ha veszünk egy, az egyenesekre párhuzamos síkmetszetet, akkor azt a feladatot kapjuk, hogy van néhány nem egyenlő távolságú pontunk a síkban, legkevesebb hány pontot kell felvennünk úgy, hogy egyenlő távolságúakat kapjunk.
Magyarul mi az a legszerencsésebb konfiguráció, amit kevés ponttal is "ki tudunk javítani". Ami még nem teljesen világos, hogy a nemegyenlőközű azt jelenti, hogy a rendezés szerinti sorrendben nem fordul elő az egymás utániak között két egyforma távolság, vagy semelyik két távolság nem azonos (bár az előbbi értelmezés szerint elég lehet akár egyetlen pontot is beszúrnunk, szóval ez nem tűnik túl logikusnak).
Meg ami még kérdés, hogy ha tényleg jól értelmezem, akkor záródnia kell-e a körnek a végén, tehát az első és utolsó közt is a megfelelő távolságnak kell-e lennie, vagy ez nem szükséges?
És bocs, ha totál félreértettem az egészet, de abból a 2 szűkszavú sorból, amit olvastam, nekem ezt sikerült összeraknom.
|
| Előzmény: [2269] Csimby, 2007-09-12 22:29:10 |
|




 b
b 1 és q
1 és q

 923076 (k=4,b=9)
923076 (k=4,b=9)
