| [2344] nadorp | 2007-09-30 20:05:12 |
 határozzik meg sin 3o pontos értékét középiskolai módszerekkel
|
|
|
|
| [2341] epsilon | 2007-09-30 16:27:08 |
 Bocs, hogy így szotyogtatom, ez még kijött, és az a sejtésem, hogy a 2 eset eredményeit kapjuk más n számok esetén is de, hogy mikor melyiket, még nem látom :-(
|
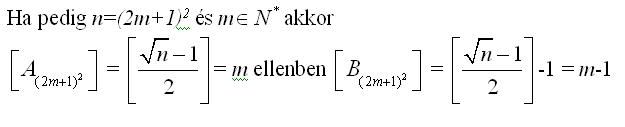 |
|
| [2340] epsilon | 2007-09-30 16:03:04 |
 Ha nem tévedtem, akkor az egészrészes eredmény páros teljes négyzet esetén mégis igaz, vagyis:
|
 |
|
| [2339] epsilon | 2007-09-30 15:26:31 |
 Igen, valóban erre sem jó, Én kicsi teljes négyzetekre, majd n=100 értékére próbáltam, ezekből próbáltam arra következtetni amit írtam, de hibásan :-( Végül is az érdekelne, hogy egyenlőek-e az An és Bn egészrészei, és mivel is egyenlőek ezek, ha n>=2 pozitív egész, és:
|
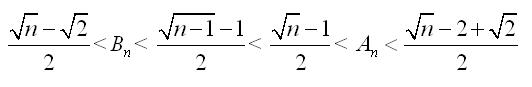 |
|
|
| [2337] epsilon | 2007-09-30 14:31:32 |
 Bocs, az egészrész nem az, és az egyenlőtlenségeket is megnézem, ha valamit elszámoltam volna.Továbbá n>2. Az egészrészes ez kell legye:
|
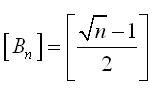 |
|
|
| [2335] epsilon | 2007-09-30 11:18:35 |
 Tisztelt Kollégák! Egy érdekes egyenlőtlenseég vezetett a következő kérdéshez: ha fennáll a következő egyenlőtlenséglánc, akkor igaz-e az egészrészre vonatkozó eredmény? Ha n négyzetszám, akkor Nekem kijött, de általában?Előre is köszönöm a válaszotokat!
|
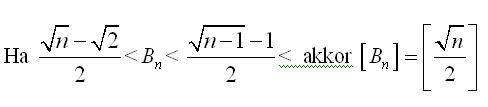 |
|
| [2334] Lbandi | 2007-09-28 20:49:15 |
 Köszönöm a válaszokat, tényleg elég nehéznek tűnik paraméteresen megadni a megoldást, egy kicsit hanyagul megfogalmazott a feladat evvel a "mi lehet lnko(x,y)?"-nal.
|
|
| [2333] Hajba Károly | 2007-09-28 00:42:05 |
 Valóban. Tegnap már nagyon késő volt és egy mondat még lemaradt. A több megoldás közül melyikre keresed az lnko-t, mert szerintem a, b, c paraméteres ismeretében ez nem egyszerű feladat.
De nézzünk egy kokrét példát:
3x+5y=61
x:y = 2:11; 7:8; 12:5 és 17:2 ha a pozitív eredményeket tekintjük. Tehát elég bonyolult függvény adhatja meg paraméteresen lnko(x,y) lehetséges értékeit.
Kicsit továbbgondoltam a feladatot, pontosabban azt, hogy mikor megoldható az alapegyenlet. Úgy tűnik, két esetben nincs megoldhatóság:
Ha (a=b)&(c 2*n*a) ill. ha páros(a,b)&páratlan(c) 2*n*a) ill. ha páros(a,b)&páratlan(c)
|
| Előzmény: [2331] Lbandi, 2007-09-27 08:56:05 |
|
| [2332] Yegreg | 2007-09-27 13:11:15 |
 Egyrészt, ax+by többszöröse (a,b)(x,y)-nak, tehát (a,b)(x,y)|c, azaz 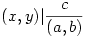 . Legyen . Legyen 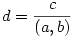 . Belátjuk, hogy d|(x,y) is lehetséges, ez ekvivalens azzal, hogy létezzen k, l egész, hogy x=kd, y=ld. Ekkor az egyenletünk akd+bld=c alakú. Legyen . Belátjuk, hogy d|(x,y) is lehetséges, ez ekvivalens azzal, hogy létezzen k, l egész, hogy x=kd, y=ld. Ekkor az egyenletünk akd+bld=c alakú. Legyen 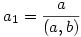 , , 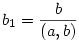 (látszik, hogy (a1,b1)=1), illetve legyen (látszik, hogy (a1,b1)=1), illetve legyen 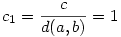 ! Az egyenletünk (a,b)d-vel való leozstás után az a1k+b1l=c1 alakot ölti, ahol a1,b1,c1 egész, tehát ez egy lineáris diofantoszi egyenlet k,l-re, továbbá (a1,b1)=1|c1, tehát az egyenletnek van is megoldása. ! Az egyenletünk (a,b)d-vel való leozstás után az a1k+b1l=c1 alakot ölti, ahol a1,b1,c1 egész, tehát ez egy lineáris diofantoszi egyenlet k,l-re, továbbá (a1,b1)=1|c1, tehát az egyenletnek van is megoldása.
Azt kaptuk tehát, hogy (x,y)|d, de van olyan x és y, hogy d|(x,y), tehát ezekre (x,y)=d.
|
|
| [2331] Lbandi | 2007-09-27 08:56:05 |
 Köszönöm a hozzászólást, de attól tartok nem lettem tőle okosabb. Azt eddig is tudtam, hogy egy ilyen egyenletnek vagy nincs megoldása, vagy végtelen sok van. A kérdés az, hogy adott a, b és c paraméterekkel mennyi lehet x és y legnagyobb közös osztója (feltételezve, hogy megoldható persze). Nyilván nem lehet akármi, hiszen legalább a c-t osztania kell a közös osztónak, de ez még nem egy kimerítő megoldás. Bocs, ha nem volt elég tiszta a feladat megfogalmazása, vagy ha valamit félreértettem a hozzászólásodban.
|
| Előzmény: [2330] Hajba Károly, 2007-09-27 01:19:51 |
|
| [2330] Hajba Károly | 2007-09-27 01:19:51 |
 Ha a*x+b*y=c egyenletnek van megoldása, akkor végtelen megoldása van, mivel a*(x-n*b)+b*(y+n*a)=c is igaz. n tetszőleges egész.
S mivel két relatív prím valahányszori összeadásával a két szám szorzatánál nagyobb bármely szám előállítható, így ha a és b relatív prímek c tetszőleges lehet, lesz az egyenletnek megoldása, s végtelen számú.
|
| Előzmény: [2329] Lbandi, 2007-09-26 21:59:47 |
|
| [2329] Lbandi | 2007-09-26 21:59:47 |
 Sziasztok! Már egy pár órája a következő feladattal bajlódok: a*x+b*y=c, lineáris diofantoszi egyenletnek létezik megoldása, azaz lnko(a,b) osztja c-t. Mennyi lehet lnko(x,y)?
Nyilván lnko(x,y) osztja c-t, de azt nem sikerült még bizonyítanom, hogy c minden osztójára létezik x,y úgy hogy lnko(x,y)=c, vagy hogy c-nek csak bizonyos osztóira (például csak c/(lnko(a,b)) osztóinak mindegyikére). Persze az is lehet, hogy nem vettem észre valami triviálisat, mindenesetre előre is köszönök minden hozzászólást :)
|
|
|
| [2327] Gyöngyő | 2007-09-25 12:25:16 |
 Köszike Nadorp!
este én is rájöttem a megoldásra,és ráadásul nem is ezt a feladatot akartam elküldeni,szerintem ennek a feladattípusnak van egy nehezebb változata.Én nem jövök rá sehogysem: 33+43+53=63 és 123+193+533=543 273+463+1973=1983 ra. Az első tagokat sikerült beazonosítanom,de a többivel van a gondom! Előre is köszönöm!
Üdv: Zsolt
|
| Előzmény: [2326] nadorp, 2007-09-25 10:24:20 |
|
|
| [2325] Gyöngyő | 2007-09-24 22:42:32 |
 Sziasztok! Tudnátok segíteni a következő feladatban: Egy összefüggést kell megsejteni: 93+123+153=183 283+533+753=843 653+1273+2483=2603
Köszönettel: Zsolt
|
|
| [2324] rizsesz | 2007-09-21 08:38:13 |
 A jó esetek azt jelentik, hogy az n. húzza ki magát az n. esetben, tehát az első n-1-et kell vizsgálni, akikre igaz, hogy egymás között senki nem húzta ki magát. Ez pedig szerintem tökéletesen reprezentálható an-1-gyel.
|
|
|
| [2322] rizsesz | 2007-09-20 15:39:46 |
 Tökéletes. :) Igazából az volt a feladat, hogy n gyerek karácsonyi ajándék-húzásba kezd, és az első n-1 embernek lehetősége van arra, hogy újra húzzon, ha önmagát húzta. A kérdés annak az volt, hogy mi annak a valószínűsége, hogy az n. ember önmagát húzza. Ezt én úgy definiáltam, hogy a jó esetek száma az, hogy az első n-1 ember nem húzza önmagát, azaz az előző értelmezésekben an-1, míg az összes eset an, így a megoldás ezek hányadosa.
|
| Előzmény: [2321] Lóczi Lajos, 2007-09-20 14:34:13 |
|
|
| [2320] rizsesz | 2007-09-20 14:23:48 |
 és akkor egyúttal a szitaformulával is ez jön ki?
|
|



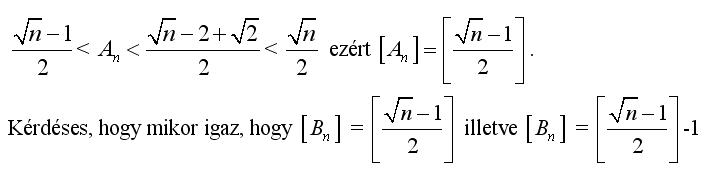
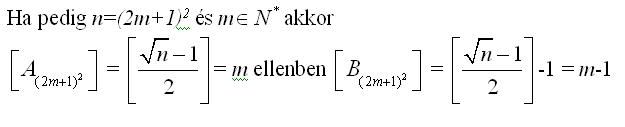

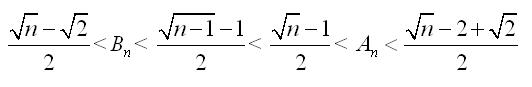
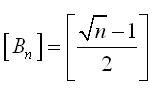
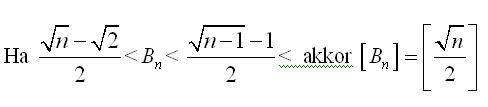

 2*n*a) ill. ha páros(a,b)&páratlan(c)
2*n*a) ill. ha páros(a,b)&páratlan(c) 


