| [2420] Hajba Károly | 2007-11-12 00:04:43 |
 No te hány lépésből tudod? 10, talán 8 vagy esetleg még ennél is kevesebb? :o)
Kiváncsi vagyok a te verziódra is. De már volt itt téma többször is. Ha nem találod, szólj, megmutatom.
|
| Előzmény: [2419] Bubóka, 2007-11-11 20:11:38 |
|
| [2419] Bubóka | 2007-11-11 20:11:38 |
 Érdekes feladat: Rajzolj csak körző segítségével adott körbe négyzetet, a lehető legkevesebb lépésből.
|
|
|
| [2417] kertitorpe | 2007-11-10 19:12:29 |
 Üdvözletem!
Van egy érdekes feladatom:
Pontosan mivel egyenlő az alábbi kifejezés?
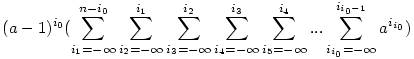 , ahol , ahol
a , n >1; n és minden ij egész
|
|
|
|
|
|
|
|
|
| [2409] Pardeller | 2007-11-04 15:21:27 |
 Hmm, furcsa... lehet, hogy kockákkal volt? most már nem vagyok túl biztos benne :S
|
|
|
|
|
| [2405] Pardeller | 2007-11-04 12:23:35 |
 Ha jól értem a feladatot, akkor tegnaphoz 11 éve ;)
Emlékszem, hogy valamikor láttam itt a fórumon a következő feladat megoldását, de nem találom. Előre is köszönöm, ha valaki oda tud irányítani, vagy le tudja esetleg újból írni a megoldást:
Bizonyítsuk be, hogy egy egész oldalhosszúságú négyzet nem bontható fel maradéktalanul nála kisebb, különböző egész oldalhosszúságú négyzetekre.
|
|
| [2404] Zsolt21 | 2007-11-04 12:19:07 |
 Üdv. mindenkinek! Én még új vagyok itt a fórumon, és lenne 1 feladványom (remélem még nem volt): Zsófi tegnapelőtt 10 éves volt, jövőre 13 lesz.Mikor született?
|
|
|
| [2402] Cckek | 2007-11-02 03:12:42 |
 oldjuk meg a funkcionalegyenletet:
f(x)=(x-y)f((x-y+1)x)+f(y)
|
|
| [2401] Lóczi Lajos | 2007-10-22 22:14:07 |
 Ha P projektor, akkor nyilván P(I-P)=(I-P)P=0, ahol I az identitás(mátrix).
A rangfeltételt figyelembe véve ezt az állítást kellene megfordítani, ebből a feladat már következne, vagyis elegendő volna igazolni, hogy
"Ha [rangfeltétel teljesül] és PR=RP=0, akkor R=I-P."
Itt persze az R:=I-Q választásra gondolok (az előzőekben ugyanis láttuk, hogy P(I-Q)=(I-Q)P=0 valóban teljesül).
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2400] Lóczi Lajos | 2007-10-22 18:07:19 |
 arxiv.org/pdf/math.RA/0003224.pdf
Ez egy 220 oldalas dokumentum, témája a projektorok rangjainak kiszámítása, kicsit nézegettem, de sajnos nem találtam benne jó formulát (bár nagyon hasonlókat igen), hátha ez segít...
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2399] Lóczi Lajos | 2007-10-22 12:32:28 |
 Egyelőre csak a következőt sikerült igazolnom: P=PQ=QP.
Jelölések: a mátrixszorzást az egymás mellé írás, a csillag a konjugált transzponáltját jelentse szokás szerint.
Feltétel szerint P2=P=P* és Q2=Q=Q*. (Ezek a vetítőmátrixok, vagy projektorok egyébként.)
Legyen A=PQ-P és számoljuk ki AA*-ot:
AA*=(PQ-P)(PQ-P)*=(PQ-P)(Q*P*-P*)=(PQ-P)(QP-P)=PQP-PQP-PQP+P=0, mert tudjuk, hogy P=PQP. De ismert, hogy AA*=0 maga után vonja, hogy A=0, azaz P=PQ. Véve ennek transzponált-konjugáltját, kapjuk, hogy P=P*=(PQ)*=Q*P*=QP.
(Nyilván a rangfeltételt nem használtam még fel, ez kellhet a továbbhaladáshoz.)
|
| Előzmény: [2391] Gyöngyő, 2007-10-20 15:49:02 |
|
|
| [2397] Gyöngyő | 2007-10-21 18:39:08 |
 Sziasztok! A hermitikus mátrix az az jeleti,hogy komplex elemű!
Üdv:
Gyögyő
|
|
|










