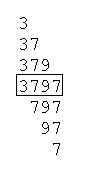|
|
| [2443] Gyöngyő | 2007-11-25 13:26:07 |
 Sziasztok!
Lenne egy kis feladatom,amivel nem nagyon tudok megbirkozni:
adva van egy általános háromszög ahol r,R a szokásos dolgok.p=kerület fele,a,b,c az oldalak hossza. Bizonyítsuk be,hogy:
a/2*((4r-R)/R)=<gyok((p-b)(p-c).
Köszönettel:
Zsolt
|
|
| [2442] Python | 2007-11-25 12:37:22 |
 a.) Nem lehet. Ha A-t csak 2 ember, B és C győzte le, akkor A-t és B-t mindkettőjüket csak C győzhette le, így B-t C legyőzi, de A-t és C-t csak B győzhette le, így C-t B legyőzi, de ez ellentmondás, így mindenkit legalább 3-an legyőznek, de ehhez 6.3=18 meccs kell, de csak 15 meccs van.
|
| Előzmény: [2439] rizsesz, 2007-11-23 10:23:55 |
|
| [2441] kisevet7 | 2007-11-23 15:26:42 |
 Sziasztok! Köszönöm a megoldásokat! Sajnálom, hogy nem voltam gépnél az előző 2 napban, így nem tudtam válaszolni a kérdésekre, de természetesen a szimmetria miatt (mármint hogy mindenki kaszabolja a másikat, csak más hatákonysággal) igaz a másik összefüggés is. Sirpi! Esetleg találkoztál azzal az ese4ttel is, ahol az egyik csapat hagyományosan kaszabol, a másik gerillaharcot folytat (amikoris a gerillákat meg is kell keresni), és ahol az összefüggés x'(t)=bx(t)y(t)? (x harcol hagyományosan, y a gerilla)
|
|
| [2440] Sirpi | 2007-11-23 14:25:47 |
 Az integrálással kapott egyenleted átrendezve:
ay2(t)-bx2(t)=ay2(0)-bx2(0)
Vagyis az f(t)=ay2(t)-bx2(t) függvény igazából nem függ t-től, és értéke ugyanannyi, mint kezdetben.
Ebből pl. kijön az a szerintem meglepő dolog, hogy egy 5000-es és egy 4000-es sereg ütközetekor (azonos tudású katonákat feltételezve) a győztes csapatnak 3000(!) katonája marad életben. 13000 vs. 12000 esetén pedig 5000.
Én biztos, hogy magamtól sokkal kevesebbre tippeltem volna (korábban magam is felvetettem és megoldottam ezt a feladatot, és már akkor megdöbbentett az eredmény).
|
| Előzmény: [2434] wernerm, 2007-11-21 22:19:43 |
|
| [2439] rizsesz | 2007-11-23 10:23:55 |
 Sziasztok!
Lehetséges-e az egy a., 6, b., 7 fős társaságban, ahol mindenki játszik mindenkivel (mondjuk sakkoznak) hogy bármely 2 emberhez található egy olyan 3., aki megverte mindkettejüket?
|
|
| [2438] nadorp | 2007-11-23 08:10:45 |
 Bocs, helyesen:
Gondolom a feladat úgy van modellezve, hogy az y sereg egy katonája mondjuk percenként "a" darab ellenséget tud legyőzni, az x sereg egy katonája pedig percenként "b" darabot és feltesszük, hogy ezt egyenletesen teszik.
|
| Előzmény: [2437] nadorp, 2007-11-23 08:06:15 |
|
| [2437] nadorp | 2007-11-23 08:06:15 |
 Gondolom a feladat úgy van modellezve, hogy az y sereg mondjuk percenként "a" darab ellenséget tud legyőzni, az x sereg pedig percenként "b" darabot és feltesszük, hogy ezt egyenletesen teszik.
|
| Előzmény: [2436] wernerm, 2007-11-22 22:22:09 |
|
| [2436] wernerm | 2007-11-22 22:22:09 |
 Ha nem lenne az az egyenlet, akkor tetszőleges y(t)-t beírhatnék, és abból x(t)-t integrálással kapnám.
A feladat kitűzője valóban nem írt y'(t) és x(t) közötti összefüggésről, de mivel két hadseregről van szó, a dolog elég szimmetrikusnak tűnik, ezért tettem fel egy ilyen alakú egyenletet.
üdv: Miklós
|
| Előzmény: [2435] Lóczi Lajos, 2007-11-22 11:44:44 |
|
|
| [2434] wernerm | 2007-11-21 22:19:43 |
 Nézzük meg, hogy az idő elteltével egymáshoz viszonyítva hogyan változnak a hadseregek. (A pontos időbeli lefutás nem lényeges, csak az a lényeg, ki nyer.)
x'(t)=-ay(t)
-bx(t)=y'(t)
Szorozzuk össze a két egyenletet!
ay(t)y'(t)=bx(t)x'(t)
Integráljuk mindkét oldalt 0-tól t-ig határozottan.
ay2(t)/2-ay2(0)/2=bx2(t)/2-bx2(0)/2
.
Átrendezve ez az x-y síkon egy hiperbola egyenlete. A végső állapotot az jelenti, ha elmetszük valamelyik tengelyt. Amelyik tengelyt elmetszettük, az a sereg győzött. (Nekik maradt katonájuk).
Az x csapat győz, ha bx2é(0)-ay2(0)>0, fordított relációnál az y csapat.
Érdekes a helyzet az egyenlőségnél. Ekkor a két sereg kölcsönösen lekaszabolja egymást.
A katonák kis létszáma esetén lényegessé válik az, hogy a katonák száma egész.
|
| Előzmény: [2433] kisevet7, 2007-11-21 20:48:07 |
|
| [2433] kisevet7 | 2007-11-21 20:48:07 |
 Tudna valaki segíteni??? A feladatom a következő: x(t) és y(t) két hadsereg létszáma. A veszteség létszáma x'(t)=-a*y(t). (a állandó)Vizsgáljuk mekkora x(0), y(0) értékeknél ki fog győzni! (Számpélda: Napóleon serege 200000 fő, Háry Jánosé 200 fő, és tudjuk, hogy Háry győzött. Mennyivel hatékonyabb egy huszár, mint egy francia?) Előre is köszönöm a segítséget! kisevet
|
|
|
|
| [2430] SmallPotato | 2007-11-15 19:03:50 |
 Az elsőhöz:
Tegyük fel, hogy 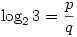 , ahol p és q egészek. , ahol p és q egészek.
Ekkor 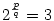 , ahonnan 2p=3q, ami azonban lehetetlen, mert a baloldal csupa 2-es, a jobboldal viszont csupa 3-as törzstényező szorzatából áll. Ezek szerint log23 nem írható fel , ahonnan 2p=3q, ami azonban lehetetlen, mert a baloldal csupa 2-es, a jobboldal viszont csupa 3-as törzstényező szorzatából áll. Ezek szerint log23 nem írható fel 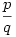 alakban. alakban.
|
| Előzmény: [2429] nemtommegoldani, 2007-11-15 18:43:44 |
|
| [2429] nemtommegoldani | 2007-11-15 18:43:44 |
 Sziasztok!Két matekfeladatom lenne, amit nme tudok megoldani, ebben szorulnék segítségre. 1. Bizonyítsd be indirekt úton, hogy a kettes alapú log3 irracionális szám! 2. Az ABC háromszög mely belső P pontja esetén lesz az a/x+b/y+c/z összeg minimális?(a,b,c a háromszög oldalai, x,y,z a P pontnak az oldalaktól való távolsága). A segítséget nagyon szépen köszönöm.
|
|
|
| [2427] Róbert Gida | 2007-11-14 18:35:23 |
 Véges sok van beőlük, sőt már azokból is, amikor csak az egyik irányból követeled meg ezt (balról haladva csak akkor, ha felteszed, hogy a számban nincsen 0 jegy). Trunctable prime kifejezésre keress rá, elég közismert probléma. A te kérdésedre a válasz, csak ezek a megoldások vannak: 2, 3, 5, 7, 23, 37, 53, 73, 313, 317, 373, 797, 3137, 3797, 739397 Ami egyébként: http://www.research.att.com/ njas/sequences/A020994.
|
| Előzmény: [2426] Python, 2007-11-14 18:00:42 |
|
| [2426] Python | 2007-11-14 18:00:42 |
 Ezt a feladatot egy barátomtól hallottam: Nevezzünk egy prímet érdekesnek, ha az elejéről vagy a végéről (egyszerre csak az egyik irányból) néhány jegyet elhagyva mindig prímet kapunk (10-es számrendszer)! Létezik-e végtelen sok érdekes prím?
Az ábrán egy 4-jegyű érdekes prím látható:
|
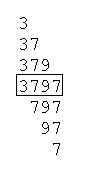 |
|
| [2425] Maga Péter | 2007-11-13 19:23:13 |
 Minden, ami szerkesztheto korzovel es vonalzoval, az szerkesztheto csak korzovel is. Lenyegeben ez a Mohr-Masceroni-tetel allitasa, a bizonyitas egyebkent meg is adja a szerkesztes lepeseit. Erdemes megtanulni az inverziot es azzal meg lehet csinalni a tetelt, egyuttal a feladatot is. Szoval hajra!
|
| Előzmény: [2423] Bubóka, 2007-11-12 19:01:38 |
|
|
| [2423] Bubóka | 2007-11-12 19:01:38 |
 Adott a kör és egy pont.
Van még egy érdekesnek tűnő feladat, amivel nem tudok mit kezdeni, de megoldható: Adott egy kör , keressük meg a középpontját csak körzővel!! ???
|
| Előzmény: [2422] jonas, 2007-11-12 18:01:24 |
|
| [2422] jonas | 2007-11-12 18:01:24 |
 Kíváncsi lennék, mi van megadva, és mi számít lépésnek. Pl. a kör középpontja adott-e, egy pont a kör kerületén ki van-e jelölve, vagy az is egy lépés.
|
| Előzmény: [2421] Bubóka, 2007-11-12 14:13:50 |
|
|