|
|
|
|
|
|
| [2539] Enkidu | 2008-01-09 12:48:33 |
 Ja igen! Elírtam, de én is igazoltam (sajnos csak magamnak) a multiplikativitást, úgyhogy ez rendben van. Igazából azért bizonytalanodtam el korábban, mert a kapott megoldás "nem valami szép" és nem tudom, hogy Cckek akar(t)-e valami szépet mutatni azzel a feladattal kapcsolatban. Én már ezen agyaltam. Csá!
|
| Előzmény: [2537] nadorp, 2008-01-09 08:32:10 |
|
| [2538] nemtommegoldani | 2008-01-09 11:21:52 |
 Sziasztok! Azt szeretném kérni, valaki írjon ide a fórumra pár "nívósabb" számelméleti feladatot legnagyobb közös osztó, ill. legkisebb közös többszörös témakörben, illetve diofantoszi egyenletek témakörben (pl. olyanokra gondolok, amik OKTV-n, vagy más tanulmányi versenyeken előfordultak már)megoldással együtt. NAgyon köszönöm a segítséget!!! Már több helyen keresgéltem, de nem nagyon találok.
|
|
|
| [2536] Enkidu | 2008-01-07 13:05:07 |
 A következő definícióval élve: 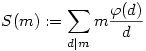 S(m) egy számelméleti függvény. Így prímhatványhelyeken felvett helyettesítési értékei meghatározzák. Ha m=pn,S(m)=pn-1(np+p-n) egyébként pedig a szokásos módon ha (m,n)=1, akkor S(mn)=S(m)S(n). S(m) egy számelméleti függvény. Így prímhatványhelyeken felvett helyettesítési értékei meghatározzák. Ha m=pn,S(m)=pn-1(np+p-n) egyébként pedig a szokásos módon ha (m,n)=1, akkor S(mn)=S(m)S(n).
Most így megnézve lehet, hogy valamit félreértettem, mert túl egyszerű amit írok, de ha már végigszenvedtem a TeX tanfolyamot csak bennhagyom. Hello!
|
| Előzmény: [2535] Cckek, 2008-01-05 12:33:11 |
|
| [2535] Cckek | 2008-01-05 12:33:11 |
 Valóban ez a megoldás, gratulálok, mert ez egyáltalán nem egy könnyű feladat:D, legalábbis számomra nem volt az. Ha már Euler számelméleti függvényénél vagyunk, akkor itt van mégegy:
Számítsuk ki a következő összeget:
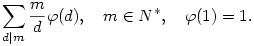
|
| Előzmény: [2534] nadorp, 2008-01-04 23:18:53 |
|
| [2534] nadorp | 2008-01-04 23:18:53 |
 Nem volt unalmas,de szerencsém volt :-). Mindkét oldal "e" alapú logaritmusát véve,bizonyítandó, hogy
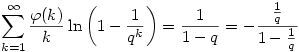
Felhasználva, hogy |q|>1 és a logaritmus függvény hatványsorát ez ekvivalens a következővel
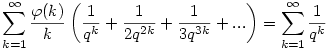 . .
Most vizsgáljuk meg 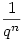 (n (n 1) együtthatóját a bal oldalon. Ha ez mindig 1, akkor készen vagyunk. 1) együtthatóját a bal oldalon. Ha ez mindig 1, akkor készen vagyunk.
Nyilván ha n=ab, akkor lesz olyan tag, ahol az együttható 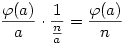 . Tehát . Tehát 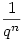 együtthatója a bal oldalon együtthatója a bal oldalon
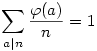 ( Itt felhasználtuk, hogy a ( Itt felhasználtuk, hogy a  (n) számelméleti függvény összegzési függvénye az "n" függvény) (n) számelméleti függvény összegzési függvénye az "n" függvény)
|
| Előzmény: [2532] Cckek, 2008-01-04 18:12:30 |
|
| [2533] Lóczi Lajos | 2008-01-04 20:33:11 |
 "Itt elég a második tagról belátni, hogy pozitív, mert az első az. x=1+t helyettesítéssel t3-ig kiírt Taylor-sorral látszik, nem tudom, van-e rá egyszerűbb módszer, ez az út elég gány ahhoz, hogy végigírjam."
Mivel csak polinom és logaritmus van benne, ilyenkor érdemes még egyszer deriválni:
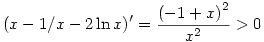 , ha x>1, de x-1/x-2ln x az 1 helyen 0, tehát ha x>1, akkor mindig pozitív a kérdéses kifejezés. , ha x>1, de x-1/x-2ln x az 1 helyen 0, tehát ha x>1, akkor mindig pozitív a kérdéses kifejezés.
|
| Előzmény: [2529] Sirpi, 2008-01-04 17:15:02 |
|
| [2532] Cckek | 2008-01-04 18:12:30 |
 Igen ez is gyors, szép megoldás, az eredeti feladat így szólt: Számitsuk ki ![\left[\frac{(e^\pi+e^e)(\pi-e)}{e^\pi-e^e}\right]](keplet.cgi?k=FF5948E8DC055B1D) -t. -t.
De mivel látom unatkoztok itt van egy sokkal nehezebb feladat amivel rengeteget kinlódtam: Bizonyítsuk be, hogy
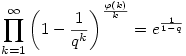
ahol  az Euler indikátor, q az Euler indikátor, q Z\{-1,0,1} Z\{-1,0,1}
|
|
| [2531] Róbert Gida | 2008-01-04 17:57:20 |
 Kijön ez deriválgatásokkal, nálam legyen x:= - - (érdemesebb ezt az utat követni, mert akkor log nem jön be). x a továbbiakban mindig legyen (0,1)-ben. (érdemesebb ezt az utat követni, mert akkor log nem jön be). x a továbbiakban mindig legyen (0,1)-ben.
Ekkor, mivel csak az egészrésze kell a függvénynek, ezért elég igazolni, hogy 2 és 3 közé esik az értéke:  , ha 0<x<1. A nevező pozitív, így felszorzás és rendezés után kapjuk, hogy kell: 0<(3-x)ex-(3+x)=:g(x), de g(0)=0, továbbá g'(x)=(2-x)ex-1, amire g'(x)>ex-1>0, így g szigorúan monoton nő (0,1) intervallumban, de g(0)=0, így g(x)>0 itt, ami kellett. (g folytonossága is kellett itt még, mert sajnos g'(0)=0). , ha 0<x<1. A nevező pozitív, így felszorzás és rendezés után kapjuk, hogy kell: 0<(3-x)ex-(3+x)=:g(x), de g(0)=0, továbbá g'(x)=(2-x)ex-1, amire g'(x)>ex-1>0, így g szigorúan monoton nő (0,1) intervallumban, de g(0)=0, így g(x)>0 itt, ami kellett. (g folytonossága is kellett itt még, mert sajnos g'(0)=0).
Másik irányú becsléshez:  , felszorozva és rendezve kell: 0 , felszorozva és rendezve kell: 0 (x-2)ex+(x+2)=:h(x), itt h(0)=0, továbbá: h'(x)=(x-1)ex+1, tehát h'(0)=0, továbbá h''(x)=xex (x-2)ex+(x+2)=:h(x), itt h(0)=0, továbbá: h'(x)=(x-1)ex+1, tehát h'(0)=0, továbbá h''(x)=xex 0, így h' monoton nő, de h'(0)=0, így h'(x) 0, így h' monoton nő, de h'(0)=0, így h'(x) 0, de akkor h monoton nő, de h(0)=0 miatt h(x) 0, de akkor h monoton nő, de h(0)=0 miatt h(x) 0 teljesül, ami kellett. 0 teljesül, ami kellett.
|
| Előzmény: [2529] Sirpi, 2008-01-04 17:15:02 |
|
|
| [2529] Sirpi | 2008-01-04 17:15:02 |
  -t kiemelve a számlálóból és a nevezőből is, valamint bevezetve az -t kiemelve a számlálóból és a nevezőből is, valamint bevezetve az 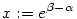 jelölést, a következő (immár egyváltozós) alakot kapjuk - mellesleg az is látszik, hogy jelölést, a következő (immár egyváltozós) alakot kapjuk - mellesleg az is látszik, hogy  és és  pozitív voltát nem használjuk sehol, az a feltétel elhagyható: pozitív voltát nem használjuk sehol, az a feltétel elhagyható:
![f(x):=\left[\frac{x+1}{x-1}\cdot \ln x \right] \qquad 1<x<e](keplet.cgi?k=36069AE35594D1F3)
f(e) 2.16, 2.16, 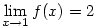 (utóbbi azért igaz, mert az x=1 közelében ln x (utóbbi azért igaz, mert az x=1 közelében ln x x-1) x-1)
Ezek után már csak az kell, hogy a függvény szigorúan monoton az [1,e] intervallumon, és meg is kaptuk a választ: 2.
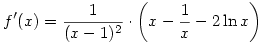
Itt elég a második tagról belátni, hogy pozitív, mert az első az. x=1+t helyettesítéssel t3-ig kiírt Taylor-sorral látszik, nem tudom, van-e rá egyszerűbb módszer, ez az út elég gány ahhoz, hogy végigírjam.
|
| Előzmény: [2528] Cckek, 2008-01-04 16:22:44 |
|
| [2528] Cckek | 2008-01-04 16:22:44 |
 Itt van Lajos, egy neked való feladat, egy helybéli igen megbecsült matematikus egyik feladatát általánosítgattam. Persze bárki megoldhatja ha van kedve hozzá.
Legyen  , , >0,0< >0,0< - - <1. Számítsuk ki <1. Számítsuk ki
![\left[\frac{(e^\beta+e^\alpha)(\beta-\alpha)}{e^\beta-e^\alpha}\right]](keplet.cgi?k=7DD0AB9D56429775)
értéket ahol [x]-el az x valós szám egész részét jelöltük.
|
|
| [2527] Lóczi Lajos | 2007-12-30 15:44:32 |
 Tovább próbálkozom. Legyenek tehát P és Q az n-dimenziós (komplex) Cn teret önmagukba képező n x n-es hermitikus idempotens mátrixok, melyek rangja azonos.
A rang a képtér dimenziója.
Az operátorokra vonatkozó felbontási tétel alapján tudjuk (felhasználva, hogy most az operátoraink hermitikusak és véges dimenzióban vagyunk), hogy Cn előáll a lineáris operátor képtere és magtere direkt összegeként. (Speciálisan, a képtér és a magtér dimenziójának összege n.)
Ezekből azt kapjuk, hogy P-nek és Q-nak nemcsak a képtere, de a magtere is azonos dimeziós kell legyen.
Korábban láttuk, hogy P=PQ. Ebből az adódik, hogy ha egy x vektor Q magterében van, akkor egyúttal P magterében is benne van: ker(Q) ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos. ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos.
De akkor a felbontási tétel miatt az ortogonális komplementereik, vagyis a képtereik is azonos alterek.
Tudjuk, hogy a projektorok a képtéren identitásként hatnak. (Valóban, ha x pl. P képterében van, akkor alkalmas y Cn vektorral x=Py. De az idempotencia miatt ekkor Px=PPy=Py=x.) Cn vektorral x=Py. De az idempotencia miatt ekkor Px=PPy=Py=x.)
Legyen tehát z egy tetszőleges Cn-beli vektor. Ekkor z előáll z0+z1 alakban, ahol z0 P magterébe esik (ami egyúttal Q magtere is), z1 pedig P (avagy Q) képterébe esik. Emiatt
Pz=P(z0+z1)=Pz1=z1=Qz1=Q(z0+z1)=Qz,
tehát P=Q.
Remélem, ezzel a megoldás rendben van :)
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2526] hobbymatekos | 2007-12-30 15:38:23 |
 Nem kőtáblába véstem:-) Azért irtam mert érdekel a téma. Semmi egyéb. Az összes tévedésre szükséges rámutatni. Az összeget azért gondolom oda a definicióhoz, mert igazán az az oldala izgat. Mint ahogy mondtad is a mátrix nyoma fontos.(Fizikailag a nyom sűrűséggel kapcsolatos. A sűrűségek pedig additivek? Vagyis egy térbeli pontban egy részecske helyett rögtön egy r szer akkora?. Helycserével? Anélkül?) Diagonálmátrixok összegének nyoma a nyomok összege. r(a+a)=raa, a mátrix elemei, r komplex számok, szintén megoldható, ekkor persze ferdén hermitikus a mátrix, akkor főátlóban tisztán képzetes szám állhat, de ezek minden páros hatványa lehet hermitikus, idempotens. De ezek csak gondolatok. Az eredeti feladattal kapcsolatban csak annyi volt a meglátásom, hogy a mátrix harmadik hatványa van a bizonyitandóban, akkor PP=P ből következik idempotencia miatt PQP=PQ=QP=PP=P. A középső rész kommutativitás. (Kommutativitásra nxn mátrixnál legalább nxn művelet kell eldöntéséhez. És ha n az Avogadro szám?) Egyébként olvasótok vagyok inkább. BUÉK
|
| Előzmény: [2524] Cckek, 2007-12-30 00:31:48 |
|
| [2525] Lóczi Lajos | 2007-12-30 14:21:01 |
 (Nem kukacoskodásból kérdeztem rá direktben, csak azért, mert nem értettem, és meg akartam érteni az állítását, ehhez tudnom kellett, a definíciókban "közös nevezőn" vagyunk-e :)
|
| Előzmény: [2524] Cckek, 2007-12-30 00:31:48 |
|
| [2524] Cckek | 2007-12-30 00:31:48 |
 Az értelmezéseket valóban kitünően elmondtad, s én hiszek abban hogy ez a forum a matematika és persze a matematikusok feltétlen tiszteletéről szól. Éppen ezért nem árt néha beismerni ha tévedtünk. Ez k...a nehéz de a tisztelet elérése szempontjából feltétlenül szükséges. És nem olyan vészes a tévedés,-a matematikai eredmények tévedések sorozatai, egy tévedés kijavítása oriási eredmény lehet:D- sokkal inkább veszélyes feltétlenül védeni az igazunkat. A magam hibájából tanultam ezt tehát, sértődöttségre semmi ok.
|
| Előzmény: [2523] hobbymatekos, 2007-12-29 02:55:18 |
|
| [2523] hobbymatekos | 2007-12-29 02:55:18 |
 Az I idempotens. Elmondtam az általános definiciot. (Annak értelmében nem lenne idempotens) Mátrixokra A=AA=AAA..... Ez a probléma amit kitűzött a kolléga: PQP=PP=P. Az állitása PQP=P alakban volt megadva. Továbbá csak vázoltam mxn mátrixból kiindulva unitér mátrixra mi adódik. Rang változatlan. Te megcsináltad Projektorra. Kellene még egy szokásos (A+A*)/2 és poláris P=QQU felbontásra is.
|
| Előzmény: [2520] Lóczi Lajos, 2007-12-28 21:08:34 |
|
|
| [2521] Lóczi Lajos | 2007-12-28 21:18:43 |
 Nem értem ezt. Kérlek, mondd ki, mi az állításod és mit bizonyítasz.
"Innen generalizálással adódik az állitás." Ez mit jelent és melyik állítás?
"P=PP=PPP implikálja TQ=TTQ implikáció ugyanaz, mint T=TQT." Ez nem magyar mondat. Kérlek, tisztázd.
Mit jelölsz felső vesszővel?
Stb.
|
| Előzmény: [2519] hobbymatekos, 2007-12-28 00:35:05 |
|





 függvénynél járunk, anno olvastam egy cikket ( Ruzsa Imre: Számelméleti függvények I.) és itt szerepel egy érdekes konstrukció. A poén az benne, hogy a multiplikatív
függvénynél járunk, anno olvastam egy cikket ( Ruzsa Imre: Számelméleti függvények I.) és itt szerepel egy érdekes konstrukció. A poén az benne, hogy a multiplikatív 
 Témakörök
Témakörök 
 1) együtthatóját a bal oldalon. Ha ez mindig 1, akkor készen vagyunk.
1) együtthatóját a bal oldalon. Ha ez mindig 1, akkor készen vagyunk.  Z\{-1,0,1}
Z\{-1,0,1} -
- (érdemesebb ezt az utat követni, mert akkor log nem jön be). x a továbbiakban mindig legyen (0,1)-ben.
(érdemesebb ezt az utat követni, mert akkor log nem jön be). x a továbbiakban mindig legyen (0,1)-ben.  (x-2)ex+(x+2)=:h(x), itt h(0)=0, továbbá: h'(x)=(x-1)ex+1, tehát h'(0)=0, továbbá h''(x)=xex
(x-2)ex+(x+2)=:h(x), itt h(0)=0, továbbá: h'(x)=(x-1)ex+1, tehát h'(0)=0, továbbá h''(x)=xex
 2.16,
2.16,  x-1)
x-1)  ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos.
ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos.