| [2583] komalboy | 2008-01-26 13:36:58 |
 h lehet azt igazolni, h a két rekurzió ugyanaz?
|
|
|
|
|
|
|
|
|
| [2575] komalboy | 2008-01-24 18:19:19 |
 Bizonyítsuk be, h a sorozat tagjai egészek:
|
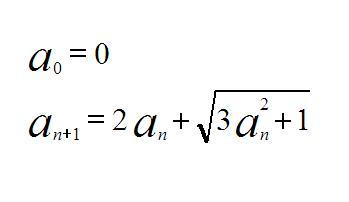 |
|
|
| [2573] Lóczi Lajos | 2008-01-24 01:48:39 |
 Igaz-e, hogy ha a,b,c tetszőleges pozitív valós számok, de a b, akkor b, akkor
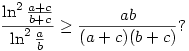
|
|
| [2572] epsilon | 2008-01-22 17:37:56 |
 Kedves Lóczi Lajos! Alaposan átnéztem a [2564]-es hozzászólásnál a megoldásodat, és úgy látom, hogy ennél elemibbet nem lehet találni, de ez amit a fogó tétellel meg a L'Hospital szabállyal függvényhatárértékből származtattál, feldolgozható a tehetségesebb, pontosabban kiváltságosn jó 12-ik osztályos tanulókkal, ellenben teljesen igazatok van, osztozom a feladatról írt véleményetekben, hogy 12. osztályban ha csak nem idomítottak be valakit ilyen trükkökre, elég nehezen jön rá ilyen megoldásra. Ismételten kösz mindkettőtöknek, nadorpnak is, hogy rávilágítottatok a feladat gyökerére is! Üdv: epsilon
|
|
|
| [2570] epsilon | 2008-01-22 06:39:13 |
 Kedves nadorp és Lajos! Köszi mindkettőtöknek a valóságos szép leckét. Én az asszimptótikus megközelítést elméletileg a Taylor-féle sorbafejtéssel képzelném el kikerülni, mondjuk a Lagrange Tételnél 1 lépéssel kellene továbbhaladni, a 2-ik rendü deriváltig az 1-ik helyett, de ez csak elképzelésem, tüzetesen átnézem amit írtatok, és ...hátha lehetne? Mégegyszer kösz Mindkettőtöknek! Üdv: epsilon
|
| Előzmény: [2568] nadorp, 2008-01-21 22:07:38 |
|
| [2569] Csimby | 2008-01-21 23:00:40 |
 Hasonlóan, mint Káli gúlának, szóval nincs benne új ötlet, csak nem tudtam továbbmenni. Azért beírom: T.f.h. ab rac., ekkor (a2+b2)(a5+b5)=a7+b7+a2b2(a3+b3) is rac., amiből köv. a2+b2 is rac. Másrészt 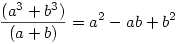 irracionalitása miatt a2-ab+b2 irrac., tehát a2+b2 irrac. Villám. irracionalitása miatt a2-ab+b2 irrac., tehát a2+b2 irrac. Villám.
|
| Előzmény: [2566] Lóczi Lajos, 2008-01-21 19:38:20 |
|
| [2568] nadorp | 2008-01-21 22:07:38 |
 Kedves Epsilon !
Nem tudom, hogy lehetne kikerülni az asszimptotikus egyenlőséget, de talán ez megfelelő lesz:
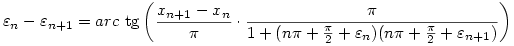
Ha most felhasználjuk, hogy az "arc tg"-ben az első tört 1-be tart, a második nevezőjének a nagyságrendje  2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés". 2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés".
|
| Előzmény: [2563] epsilon, 2008-01-21 17:16:39 |
|
| [2567] nadorp | 2008-01-21 21:45:23 |
 Lajos megoldása rövidebb, de álljon itt az enyém is.( Ha túl hosszú és unalmas, akkor hagyjátok ki.)
Azt láttuk, hogy
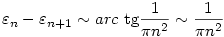
Tehát tetszőlesges  >0-hoz létezik N, ha n>N, akkor >0-hoz létezik N, ha n>N, akkor
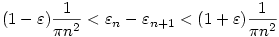
Ezt elvégezve az n+1,...,n+k-1 számokra is és összeadva a k db egyenlőtlenséget
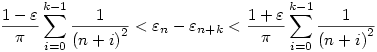
Ha most felhasználjuk,hogy
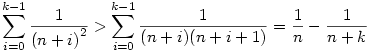 és hogy és hogy
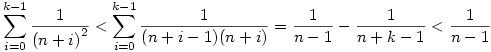 akkor akkor
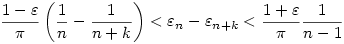 teljesül minden k-ra.Ha k=n2 teljesül minden k-ra.Ha k=n2
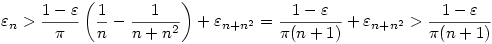 Másrészt Másrészt
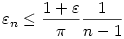 is igaz, ui. ellenkező esetben is igaz, ui. ellenkező esetben
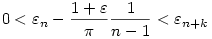 igaz lenne minden k-ra, de ez ellentmond a 0-ba tartásnak. Tehát igaz lenne minden k-ra, de ez ellentmond a 0-ba tartásnak. Tehát
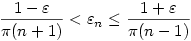
|
| Előzmény: [2563] epsilon, 2008-01-21 17:16:39 |
|
|
| [2565] Lóczi Lajos | 2008-01-21 19:36:40 |
 Ez tehát azt mutatja, hogy a fixpontegyenlet gyökei aszimptotikusan
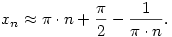
Kíváncsiságból egy lépéssel tovább is kiszámoltam, az előzőhöz hasonló érveléssel (a nehézség nem nőtt), és azt kaptam, hogy

|
| Előzmény: [2564] Lóczi Lajos, 2008-01-21 19:29:01 |
|
| [2564] Lóczi Lajos | 2008-01-21 19:29:01 |
 Tényleg nem értem, hogy lehetne ez egy tesztkérdésben benne (amikor, ahogyan illusztráltam, sok 18 évesnek problémája van a törtekkel és hatványozás azonosságaival...)
Szóval technikailag kicsit talán egyszerűbb így elmondani:
xn=n + + /2- /2- n, ebből egyszerűen kapjuk (figyelembe véve, hogy xn melyik intervallumban van, illetve hogy xn melyik egyenlet megoldása), hogy n, ebből egyszerűen kapjuk (figyelembe véve, hogy xn melyik intervallumban van, illetve hogy xn melyik egyenlet megoldása), hogy
 /2-arctg(n /2-arctg(n + + /2- /2- n)= n)= n. n.
Most használjuk fel, hogy 0< n< n< /2 (de konkrét becslés nem is kell, elegendő annyit tudnunk, hogy /2 (de konkrét becslés nem is kell, elegendő annyit tudnunk, hogy  n korlátos, hiszen nullsorozat). Ekkor n korlátos, hiszen nullsorozat). Ekkor  /2-arctg(n /2-arctg(n + + /2- /2- n) alulról és felülről becsülhető n) alulról és felülről becsülhető  /2-arctg(n /2-arctg(n +konstans) alakú kifejezésekkel, használva az arkusz tangens monotonitását. Ezt most már valós x-ekre kiterjesztve, a L'Hospital-szabállyal egy deriválás után látszik, hogy +konstans) alakú kifejezésekkel, használva az arkusz tangens monotonitását. Ezt most már valós x-ekre kiterjesztve, a L'Hospital-szabállyal egy deriválás után látszik, hogy
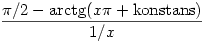
limesze (x tart végtelen esetén, tetszőleges, rögzített "konstanssal") 1/ , a közrefogási elv miatt az előző bekezdés értelmében tehát n , a közrefogási elv miatt az előző bekezdés értelmében tehát n n határértéke valóban 1/ n határértéke valóban 1/ . .
|
| Előzmény: [2563] epsilon, 2008-01-21 17:16:39 |
|
| [2563] epsilon | 2008-01-21 17:16:39 |
 Helló nadorp! A feleletválasztós tesztben ahonnan a feladat származik lehetséges válaszok: 1, 0, 1/pi, pi/2, pi/4 és ahogy nézem, az asszimptótikus megközelítéseid alapján 1/pi lenne...csak az a gondom, hogy nem igazán látom az utolsó 2 sorodban honnan vannak az asszimptótikus megközelítések, na meg hogyan lehetne ezt a feladatot 12. osztályt végzettnek feladni (mert az kapta fel) hiszen az asszimptótikus megközelítés nincs a tananyagban...szóval vajon hogyan lehetne a megoldást leszállítani 12. osztályos szintre? Üdv: epsilon
|
|
|
|
|
|





 B
B 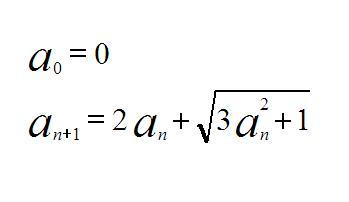

 b, akkor
b, akkor 
 2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés".
2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés". >0-hoz létezik N, ha n>N, akkor
>0-hoz létezik N, ha n>N, akkor 