| [2645] Sirpi | 2008-05-15 22:39:14 |
 Szerintem ezt a négyzetfelosztást mindig meg lehet csinálni akkor is, ha a két kis négyzet (egész) oldalhosszát előírjuk (a és b). Hiszen ekkor egy ab(a2+b2) oldalhosszú négyzet biztos kitölthető, méghozzá úgy, hogy a felső részében vannak az a oldalhosszú kis négyzetek (b(a2+b2)×a db.), alatta pedig a b oldalúak (a(a2+b2)×b db.). Sőt, gyakran kevesebb is elég lehet, pl. ha a és b nem relatív prím. Viszont azt nem tudom, hogy ennél kevésbé rendezett megoldások is vannak-e kisebb elemszámmal.
|
| Előzmény: [2643] Lóczi Lajos, 2008-05-15 21:51:46 |
|
| [2644] jonas | 2008-05-15 22:23:31 |
 A négyzetes nem nehéz.
Egyszerűen választunk egy (s,a,x) számhármast, amelyre 1<s,x és 0<x<a2, és a2-x=s2x. Ezután egy nagy négyzetet felosztunk a2 közepes négyzetre, majd x darab közepes négyzetet egyenként s2 darab kis négyzetre.
Több megfelelő számhármas is van, az ábra a (2,5,5)-nek megfelelő megoldást mutatja, de jó például a (2,10,20),(3,10,10),(7,10,2),(2,15,45),(4,17,17),(2,20,80),(3,20,40),... is.
Ha 4s2 x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja. x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja.
|
 |
| Előzmény: [2643] Lóczi Lajos, 2008-05-15 21:51:46 |
|
| [2643] Lóczi Lajos | 2008-05-15 21:51:46 |
 Hát akkor tűzzük ki :) Az is érdekes kérdés, hogy határértékben mi a fekete/fehér kockák aránya, az optimális esetben, ha a négyzetrács mérete végtelenhez tart. Amúgy ezt a feladatot idén adták fel orosz 6.-osoknak, egy olimpiai előkészítőn. A közölt megoldás is 28-at ad meg (egyébként Python ábráján a jobb szélsőt), persze nem bizonyítja az optimalitást. (A feladat pontozása érdekes: aki 25 autót rak be, 1 pontot kap, ezen felül viszont minden újabb autó plusz 2 pontot ér :-)
A másik, hasonlóan érdekes feladat: osszunk fel egy négyzetet kétféle méretű négyzetre, úgy, hogy a két fajtából egyforma számú darab szerepel. Kíváncsi vagyok, hogy van-e lényegében másfajta elrendezés, mint amit közöltek.
(A többi 4 feladat triviális volt ezekhez képest.)
|
| Előzmény: [2642] Python, 2008-05-15 19:55:25 |
|
| [2642] Python | 2008-05-15 19:55:25 |
 A 28 nálam is megvan és szerintem nincs ennél jobb, mivel elég sokat szórakoztam, és 28-at többfélét találtam, de annál jobbat nem (3 példányt felteszek ábrában). Érdekes lenne a feladatot általánosabban is kitűzn, tehát n×n-es parkolóra.
|
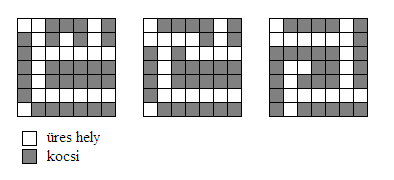 |
| Előzmény: [2640] Káli gúla, 2008-05-15 14:50:44 |
|
| [2641] Róbert Gida | 2008-05-15 16:48:03 |
 Jók a számok. Lehet találni egy formulát, ami ilyen számokat állít elő, feltéve, hogy néhány szám prím a formulában. Ez hasonló a Carmichael számokat gyártó képlethez, ami persze nem véletlen, hiszen ahogy írtad ezek mind azok. Ha egy ikerprím sejtéshez hasonló sejtés igaz, akkor máris végtelen sok ilyen szám van.
|
| Előzmény: [2638] Enkidu, 2008-05-15 12:41:43 |
|
|
|
| [2638] Enkidu | 2008-05-15 12:41:43 |
 Ha jól számoltam az első két szám: 1729 és 2465 (a harmadik a 15841). A "bizonyításom" egy program, ami végigfut a Carmichael-számokon (csak ilyenek lehetnek a feladatban kitűzött számok).
Hogy miért éppen a Carmichael-számok?! Azok az n számok, melyekre minden lnko(a,n) = 1 esetén an-1 1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség. 1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség.
Most hirtelenjében csak azokon a számokon fut a progi, amik beleférnek a szabvány 16-bites (max 32000) egész szám fogalmába. Arra nem merek tippelni, hogy véges, vagy végtelen sok ilyen szám van.
Üdv!
|
| Előzmény: [2633] Róbert Gida, 2008-04-28 19:11:45 |
|
| [2637] Lóczi Lajos | 2008-05-13 12:14:17 |
 Egy 7x7-es autóparkolóba legfeljebb hány darab autót helyezhetünk el, ha azt akarjuk, hogy bármelyik ki tudjon jönni a többitől függetlenül? (A kijárat bal fölül van, és egyszerre mindig csak 1 autó mozog. 1 autó 1 teljes négyzetet foglal el és csak a négyzetrács mentén mozoghatnak függőlegesen vagy vízszintesen.)
|
 |
|
|
| [2635] Róbert Gida | 2008-05-12 01:35:06 |
 Ha valaki ki akarná számolni: Monte Carlo módszere kb. 0.177-et ad az integrálra, 1 millió pontot használva az egységnégyzetből, ez így kb. 1/sqrt(1000000)=1/1000-ed pontosságot jelent.
|
| Előzmény: [2634] Gyöngyő, 2008-05-12 00:58:33 |
|
| [2634] Gyöngyő | 2008-05-12 00:58:33 |
 Mennyi a következő integrál értéke: Ahol a kapcsos zárójel törtrészt jelent:
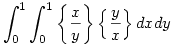
Üdv.: Zsolt
|
|
| [2633] Róbert Gida | 2008-04-28 19:11:45 |
 Találjuk meg a két legkisebb pozitív egész 1-nél nagyobb páratlan N számot, melyre teljesül, hogy: minden lnko(a,N)=1 esetén 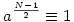 mod N teljesül! Mi a sejtésünk: végtelen vagy véges sok ilyen N szám van? mod N teljesül! Mi a sejtésünk: végtelen vagy véges sok ilyen N szám van?
|
|
|
| [2631] Róbert Gida | 2008-04-27 00:52:00 |
 Egy megoldás rá: Legyen s=a1+an rögzített, ekkor, ha s fix, akkor a jobb oldal is fix. De mi lesz a bal oldal maximuma (rögzített s esetén)? Legyen x=a2...ak és y=an-k+1...an-2, a bal oldalon elég az első és utolsó tagot nézni:
max(a1*x+y*an)=max(x,y)*s, ha s=a1+an, és a maximum felvétetik olyan helyen (is), ahol a1=0 vagy an=0, ezt beírva az eredeti feladatot kapjuk meg csak n tag helyett (n-1) taggal. Azaz leszállhatunk, egészen n=k-ig, ami a triviális eset, hiszen ez éppen a számtani-mértani egyenlőtlenség.
Egyenlőség viszont sokféleképpen lehet, például k=1-nél mindig egyenlőség van. n=3,k=2-nél pontosan akkor, ha a1-a2+a3=0
|
| Előzmény: [2630] Gyöngyő, 2008-04-26 22:06:26 |
|
| [2630] Gyöngyő | 2008-04-26 22:06:26 |
 Szisztok!
Legyen k és n pozitiv egészek és k=<n, és legyen a1,a2,...an nemnegativ valós számok. Bizonyítsuk be,hogy
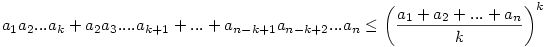
|
|
| [2629] Ratkó Éva | 2008-04-21 13:16:07 |
 Kedves CD iránt érdeklő és tájékozott fórumozók! Az, hogy a KöMaL eltűnt a sulinet honlapról, sajnos nem a mi hatáskörünk: higgyétek el, mi is azt szeretnénk, ha még mindig ott lenne. Volt velük egy ötéves szerződésünk, melyet a lejárta után nem óhajtottak megújítani, és jelenleg is ez az állapot áll fenn. Valóban, szkennelt formában elérhetőek a számok a mi honlapunkon, teljesen ingyen. (Itt egy másik oldal is, ahol elérhetők, méghozzá oldalanként: db.komal.hu/scan ) Ahhoz, hogy a) vagy egy hasonlóan működő honlapot gyártsunk b) a CD-t frissítsük vagy internetes vagy új CD-kiadás formájában, egy jó programra és ehhez pénzre van szükségünk. A HEFOP pályázat arról szólt, hogy adatokkal feltöltjük az adatbázisunkat.
Egyébként a pályázatnak 2006 decemberében vége volt, azóta még nem kaptuk meg az általunk kifizetett pénz 20%-át. Tehát adott egy egész szépen feltöltött adatbázis, amivel még 2 teendő van - ez folyik most- : 1.) a szöveghez az ábrákat bevinni - ezt elkezdték, de nem fejezték be - 2.) ellenőrizni kell, hogy tényleg jók-e a bevitt szövegek - ugyanis az adatbevitelkor sok hiba keletkezhetett.
Valóban eladtunk kb. 500 Cd-t, ebből számoljátok ki hány ember fizetése (minimálbér) finanszírozható!? Hány hónapig? (persze a CD nyomása és elkészítése és az azt működtető valóban nem egészen felhasználóbarát program megíratása sem volt ingyen - amúgy épp ezért szándékoznánk valami mai igényeknek megfelelőbb feldolgozást) Szóval elnézést, de ma csak itt tartunk. Egyébként teljesen igazatok van, már rég működnie kéne ennek az archívumnak valamilyen formában. A jó hír az, hogy legalább a KöMaL kiadására és a KöMal-honlap és FÓRUM működtetésére épp hogy futja a MATFUND (és az adófizetők) pénzéből :-)
Oláh Vera
|
| Előzmény: [2626] Cogito, 2008-04-13 14:11:36 |
|
| [2628] sakkmath | 2008-04-13 16:17:36 |
 Szia Gyöngyő!
Úgy tűnik, az első öt jól felírt sorozattag után a sok szám és vessző között eltévedtél, s talán ezzel magyarázható, hogy több hibával írtad fel a sorozat hátralévő tagjait. Megpróbálom hiba nélkül leírni a sorozat első 11 tagját, remélem, sikerül: 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, 31131211131221, 13211311123113112211, 11131221133112132113212221, ...
Végül nézzük a rekurziós képzési szabályt; hogyan kapjuk a 11. tagot a tizedikből: 1db 1, 1db 3, 1db 2, 2db 1, 1db 3, 3db 1, 1db 2, 1db 3, 2db 1, 1db 3, 2db 1, 2db 2, 2db 1.
Üdv: sakkmath
|
| Előzmény: [2627] Gyöngyő, 2008-04-13 14:36:32 |
|
| [2627] Gyöngyő | 2008-04-13 14:36:32 |
 Sziasztok!
Van egy jópofa feladatom!
folytasd:
1,11,21,1211,111221,31,2211,13112221,1113213211,31131211321, 132113111231131211....
üdv: Zsolt
|
|
| [2626] Cogito | 2008-04-13 14:11:36 |
 A KöMaL-szerkesztőség erről csak ennyit ír. E szűkszavú híren kívül illett volna azt is közölni, hogy a mostani állapot mégis meddig tart, illett volna megindokolni a "nem elérhető"-ség okát, s végül, de nem utolsó sorban, illett volna elnézést is kérni a legalább másfél éve tartó, bosszantó helyzetért.
Szerencsére van egy lehetőség, hogy saját cd-t készítsünk a KöMaL első 100 évének archívumáról. A hogyanhoz klikk ide. (Egy 523 MB-os ZIP-állományt kell/lehet letölteni...)
Az utóbbi linken a 2005 nyarán megjelent "Irány a Nobel-díj KöMaL 1994-2003" című CD-ről többek között ez olvasható: " ... minden vásárlót regisztrálunk, és számukra a jövőben lehetővé tesszük, hogy a folyamatosan bővülő tartalmat a meglevő CD-jük frissítéseként letölthetik erről a web-címről ...". A közlemény így zárul: "Az összes megjelent füzet digitalizálása körülbelül 3 évet vesz majd igénybe."
Ezek alapján joggal kérdezhetik a regisztrált felhasználók, hogy:
1) Az eltelt csaknem 3 év alatt miért nem lehetett semmiféle frissítést letölteni?
2) Az óvatos "körülbelül 3 év" hány év lesz a valóságban?
|
| Előzmény: [2625] kdano, 2008-04-11 19:47:08 |
|
|
|
|
| [2622] Lóczi Lajos | 2008-03-23 22:25:16 |
 Elegáns. Egy másik megközelítés lehet, ha a Róbert Gida által felvázolt módon expliciten kiszámoljuk a szóban forgó 5 darab, közönséges 3-dimenziós tetraéder térfogatnégyzetét: ez nagyon egyszerű pl. (a Héron-képletet is általánosító) Cayley-Menger determinánsok segítségével.
|
| Előzmény: [2621] Káli gúla, 2008-03-23 21:16:30 |
|
|




 x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja.
x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja. 


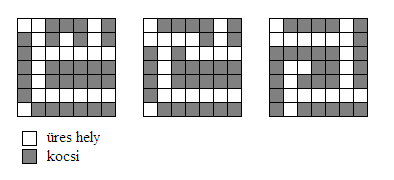



 1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség.
1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség. 
 2 gondolom így sokat segít.
2 gondolom így sokat segít.


