|
| [2657] leni536 | 2008-05-26 12:14:58 |
 Ebben az utóbbiban a határ 1 lesz. 1 alatt van stratégiám a nyúl számára. Ha pont 1, akkor a farkasok nyernek.
Az eredeti feladatban nálam is 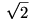 , de én sem lőném le a poént, leginkább mert lusta vagyok begépelni, meg mert alapvetően fizikus vagyok és úgysem tudom úgy leírni, hogy egy matekos ne tudjon belekötni. :P , de én sem lőném le a poént, leginkább mert lusta vagyok begépelni, meg mert alapvetően fizikus vagyok és úgysem tudom úgy leírni, hogy egy matekos ne tudjon belekötni. :P
|
| Előzmény: [2656] Enkidu, 2008-05-26 11:58:20 |
|
| [2656] Enkidu | 2008-05-26 11:58:20 |
 Hello!
Megvan a megoldás, feltéve, ha az állatok pontszerűnek tekinthetők (a határ - a sebességek arányára, ha jól sejtem 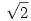 ); nem lőném le még a "poént", bár a zárójeles rész beszédes lehet. ); nem lőném le még a "poént", bár a zárójeles rész beszédes lehet.
Nekem az jutott eszembe a feladat kapcsán, hogy mi a helyzet, ha a farkasok a négyzet oldalfelező pontjaiban vannak, a nyuszi pedig a négyzet közepén? Első blikkre ez utóbbit nem tudom megválaszolni.
Ui.: Volt Szegeden az egyetemen egy tanárom dr. Pintér Lajos, aki mindig bátorított minket arra, hogy a legegyszerűbb példákat is általánosítsuk, egy kicsit változtassuk meg, kóstolgassuk... ergo kísérletezgessünk vele. Ő (pedig marha nagy koponya) soha nem bánta, ha egy-egy példa "gagyi", egyfelől mindig van, akinek nem az, másfelől tovább gondolva szép példák, általánosítások kerekedhetnek ki belőle. Bocs, ha szószátyár voltam, sziasztok!
|
| Előzmény: [2654] Cckek, 2008-05-25 08:51:21 |
|
|
| [2654] Cckek | 2008-05-25 08:51:21 |
 Egy érdekes feladat, ami szépen általánosítható és több kérdést is von maga után:
Egy négyzet alakú kert közepén ül egy nyuszi, a kert négy sarkában egy-egy farkas. A farkasok 1,4-szer gyorsabban futnak a nyúlnál, de csak a kert határa mentén mozoghatnak. Kijuthat-e a nyúl a kertből? Mennyi a nyúl és farkas sebességének a minimális aránya, mikor kijuthat?
Előre is elnézést ha a feladat túl egyszerű vagy gagyi:D
|
|
| [2653] Lajosz | 2008-05-19 16:15:27 |
 Köszönöm Sirpi!
A lenti számháromszög két utolsó sora a 12 és 13 esetét írja le, azok már nem fértek el egy sorba...
Értelemszerűen az előző sorok számainak összegei (felfelé haladva) 3 - nak 11, 10, 9,...1, 0 hatványai.
Ez emlékeztet a permutációk fixpontjaira! Az ismétléses variáció fixpontjaira van valahol irodalom?
A bal oldali oszlop:1 2 4 8 16...mint a permutációknál: a nulla fixpontok darabszámát jelentené. majd jobbra haladva az egy, kettő, stb fixpontok darabszámát!
Egyáltalán van ilyen fogalom? Ha van milyen néven keressem?
Mert ez, ha általánosítjuk, "m" alapú hatvánnyal leírható minden ismétléses variációra igaz!
m=3
1
2, 1
4, 4, 1
8, 12, 6, 1
16, 32, 24, 8, 1
32, 80, 80, 40, 10, 1
64, 192, 240, 160, 60, 12, 1
128, 448, 672, 560, 280, 84, 14, 1
512, 2304, 4608, 5376, 4032, 2016, 672, 144, 18, 1
1024, 5120, 11520, 15360, 13440, 8064, 3360, 960, 180, 20, 1
2048, 11264, 28160, 42240, 42240, 29568, 14784, 5280, 1320, 220, 22,1
4096, 24576, 67584, 112640, 126720, 101376, 59136, 25344, 7920, 1760, 264, 24, 1
8192, 53248, 159744, 292864, 366080, 329472, 219648, 109824, 41184, 11440, 2288, 312, 26, 1
lásuk m=4 esetén!
1
3, 1
9, 6, 1
27, 27, 9, 1
81, 108, 54, 12, 1
243, 405, 270, 90, 15, 1
729, 1458, 1215, 540, 135, 18, 1
2187, 5103, 5103, 2835, 945, 189, 21, 1
Maple kóddal:
** :a hatvány jele.
for i from 0 to 13 do seq(binomial(i, j)*3**(i-j), j = 0 .. i) od;#
3**(i-j) > itt a 3 egyenlő m=4 minusz egy, etc...
|
| Előzmény: [2652] Sirpi, 2008-05-19 10:47:20 |
|
| [2652] Sirpi | 2008-05-19 10:47:20 |
 A rendes 13-as totón a pontosan k találat darabszáma:
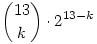
Hiszen kiválasztjuk azt a k meccset, amit eltalálunk, azok kitöltése egyértelmű, a többinél pedig mindenhol 2 lehetőségünk van, hogy oda rosszat írjunk. Ha fix meccsek is vannak, akkor a képletben mindkét 13-ast cseréld ki tetszőleges kisebb számra (mondjuk az nem teljesen világos, hogy a fix találatokat miért nem számolod a találatok közé, mert azt írod, hogy 12-ből maximum 12 találatod lehet, de mivel így szeretnéd értelmezni, ennek megfelelően adtam meg a képletet).
|
| Előzmény: [2651] Lajosz, 2008-05-19 10:40:06 |
|
| [2651] Lajosz | 2008-05-19 10:40:06 |
 Ismétléses variáció:
A totón, ha minden esetet megjátszunk, (3 a 13-on ), mennyi 0, 1, 2,...11, 12, 13. találatunk lesz, hogyan kell kiszámítani?
Ugyanezt hogyan számítjuk, ha 1 fix mérkőzés mellett (3 a 12-en) eredményt megjátszunk, mennyi 0, 1, 2,...11, 12. találatunk lesz?
etc...
|
|
|
| [2648] Sirpi | 2008-05-16 02:27:20 |
 És hogy ez miért optimális:
A közlekedőutat tekintsük egy gráfnak (a csúcsok az üres mezők, az élek az élszomszédos mezőket kötik össze). Erről a gráfról kell belátni, hogy ha nem is mindig összefüggő, de néhány autó átpakolásával mindig azzá tehető. Hiszen ha van út, ami nincs összeköttetésben a bal felső sarokkal (az ábrán a sárga tartomány), akkor az annyit jelent, hogy egy vagy több autó blokkolja az utat a bal felső sarokig. Vegyünk egy ilyen autót (piros), és toljunk rajta egyet, rá a belső útra (kék helyzet). Az autó az új helyzetében nem blokkolhat másik autót, hiszen az autók hiába hajtanak a belső útra, onnan nem tudnak kijutni, csak ha az eredeti helyükre visszamennek, tehát a kék mező érintése nélkül is ki tudnak jutni, ha eddig ki tudtak. A kék autó pedig szintén kijut (egyet előremegy, és onnan már a feltételezésünk szerint kijut). Ezzel a tolással a belső út hossza 1-gyel csökkent, így ilyen lépések véges sorozatával felszámolható az összes belső út (jelen esetben a kék autót még 1-gyel lejjebb tolva a belső út összekapcsolódik a "fő" úthálózattal, vagyis több lépésre nincs is szükség).
Így a továbbiakban feltehető, hogy a közlekedőutak hálózata összefüggő, álljon k mezőből. Ekkor legalább k-1 belső kapcsolódása van (az összefüggő gráfnak legalább k-1 éle van). Minden belső kapcsolódás 2-vel csökkenti a közlekedőhálózat kerületét, tehát az összkerület legfeljebb 4k-2(k-1)=2k+2. Minden él a kerületen egy autónak ad lehetőséget, hogy felhajtson az úthálózatra, és így eljusson a bal felső sarokba (egy autó több élen át is megteheti ezt). Sőt, a bal felső mező két sarokéle nem segít egy autónak sem, vagyis legfeljebb 2k autó lehetséges k mezőből álló úthálózat esetén. Tehát a mezők számának legfeljebb 2/3-án lehetnek autók, és ez az arány aszimptotikusan (az előző hsz. ábrája alapján) el is érhető.
Megj.: Sőt, az út "meglátogatja" a másik 3 sarkot is, hiszen egy sarok és két szomszédja közül nem állhat mind a 3-on autó, vagyis k mezőből álló úthálózat esetén legfeljebb 2k-3 autó lehetséges (hiszen minden határélnél vesztünk egy autót) - feltéve, hogy a parkoló mindkét oldalának hossza legalább 4, mert ilyenkor a sarkokkal szomszédos mezők nem eshetnek egybe.
|
 |
| Előzmény: [2649] Sirpi, 2008-05-16 01:37:44 |
|
|
|
| [2646] Róbert Gida | 2008-05-15 23:35:28 |
 Szerintem nem adható rá explicit képlet tetszőleges n-re. Programozási versenyen volt egy hasonló példa axb-es téglalapra, de úgy, hogy alul és felül is ki lehet jutni, gyakorlatilag végignézték az összes esetet a megoldásoknál.
Ha az első ábrában a hatodik sor első pozicióján nem autó van, és ilyen 7x7-es blokkokat rakunk egymásra, akkor tetszőleges autó fel tud jutni a legfelső sorba. Ha a nagy négyzet felső sorából töröljük az autókat, így már mindenki kijut, ez (7k)x(7k)-asra müködik, ha n nem ilyen alakú, akkor legyen k=floor(n/7). Az autók száma aszimptotikusan 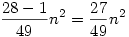 . .
Felső becslés pedig: egy autónak van van legalább egy nem autó szomszédja, hogy esélye legyen kijutni (kivéve, ha n=1 és 1 autó van az ábrán), továbbá egy nem autó hely maximum 3 autónak lehet szomszédja, ami kijutásra használja, ellenben minden szomszéd autó, de akkor nem tudna kijutni, ha odamenne. Így #autó<=3*#nemautó, azaz
#auto<=3*(n2-#auto), innen 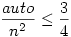 teljesül, ha n>1. teljesül, ha n>1.
|
| Előzmény: [2643] Lóczi Lajos, 2008-05-15 21:51:46 |
|
| [2645] Sirpi | 2008-05-15 22:39:14 |
 Szerintem ezt a négyzetfelosztást mindig meg lehet csinálni akkor is, ha a két kis négyzet (egész) oldalhosszát előírjuk (a és b). Hiszen ekkor egy ab(a2+b2) oldalhosszú négyzet biztos kitölthető, méghozzá úgy, hogy a felső részében vannak az a oldalhosszú kis négyzetek (b(a2+b2)×a db.), alatta pedig a b oldalúak (a(a2+b2)×b db.). Sőt, gyakran kevesebb is elég lehet, pl. ha a és b nem relatív prím. Viszont azt nem tudom, hogy ennél kevésbé rendezett megoldások is vannak-e kisebb elemszámmal.
|
| Előzmény: [2643] Lóczi Lajos, 2008-05-15 21:51:46 |
|
| [2644] jonas | 2008-05-15 22:23:31 |
 A négyzetes nem nehéz.
Egyszerűen választunk egy (s,a,x) számhármast, amelyre 1<s,x és 0<x<a2, és a2-x=s2x. Ezután egy nagy négyzetet felosztunk a2 közepes négyzetre, majd x darab közepes négyzetet egyenként s2 darab kis négyzetre.
Több megfelelő számhármas is van, az ábra a (2,5,5)-nek megfelelő megoldást mutatja, de jó például a (2,10,20),(3,10,10),(7,10,2),(2,15,45),(4,17,17),(2,20,80),(3,20,40),... is.
Ha 4s2 x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja. x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja.
|
 |
| Előzmény: [2643] Lóczi Lajos, 2008-05-15 21:51:46 |
|
| [2643] Lóczi Lajos | 2008-05-15 21:51:46 |
 Hát akkor tűzzük ki :) Az is érdekes kérdés, hogy határértékben mi a fekete/fehér kockák aránya, az optimális esetben, ha a négyzetrács mérete végtelenhez tart. Amúgy ezt a feladatot idén adták fel orosz 6.-osoknak, egy olimpiai előkészítőn. A közölt megoldás is 28-at ad meg (egyébként Python ábráján a jobb szélsőt), persze nem bizonyítja az optimalitást. (A feladat pontozása érdekes: aki 25 autót rak be, 1 pontot kap, ezen felül viszont minden újabb autó plusz 2 pontot ér :-)
A másik, hasonlóan érdekes feladat: osszunk fel egy négyzetet kétféle méretű négyzetre, úgy, hogy a két fajtából egyforma számú darab szerepel. Kíváncsi vagyok, hogy van-e lényegében másfajta elrendezés, mint amit közöltek.
(A többi 4 feladat triviális volt ezekhez képest.)
|
| Előzmény: [2642] Python, 2008-05-15 19:55:25 |
|
| [2642] Python | 2008-05-15 19:55:25 |
 A 28 nálam is megvan és szerintem nincs ennél jobb, mivel elég sokat szórakoztam, és 28-at többfélét találtam, de annál jobbat nem (3 példányt felteszek ábrában). Érdekes lenne a feladatot általánosabban is kitűzn, tehát n×n-es parkolóra.
|
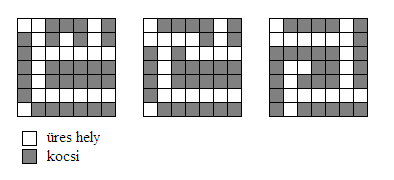 |
| Előzmény: [2640] Káli gúla, 2008-05-15 14:50:44 |
|
| [2641] Róbert Gida | 2008-05-15 16:48:03 |
 Jók a számok. Lehet találni egy formulát, ami ilyen számokat állít elő, feltéve, hogy néhány szám prím a formulában. Ez hasonló a Carmichael számokat gyártó képlethez, ami persze nem véletlen, hiszen ahogy írtad ezek mind azok. Ha egy ikerprím sejtéshez hasonló sejtés igaz, akkor máris végtelen sok ilyen szám van.
|
| Előzmény: [2638] Enkidu, 2008-05-15 12:41:43 |
|
|
|
| [2638] Enkidu | 2008-05-15 12:41:43 |
 Ha jól számoltam az első két szám: 1729 és 2465 (a harmadik a 15841). A "bizonyításom" egy program, ami végigfut a Carmichael-számokon (csak ilyenek lehetnek a feladatban kitűzött számok).
Hogy miért éppen a Carmichael-számok?! Azok az n számok, melyekre minden lnko(a,n) = 1 esetén an-1 1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség. 1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség.
Most hirtelenjében csak azokon a számokon fut a progi, amik beleférnek a szabvány 16-bites (max 32000) egész szám fogalmába. Arra nem merek tippelni, hogy véges, vagy végtelen sok ilyen szám van.
Üdv!
|
| Előzmény: [2633] Róbert Gida, 2008-04-28 19:11:45 |
|
| [2637] Lóczi Lajos | 2008-05-13 12:14:17 |
 Egy 7x7-es autóparkolóba legfeljebb hány darab autót helyezhetünk el, ha azt akarjuk, hogy bármelyik ki tudjon jönni a többitől függetlenül? (A kijárat bal fölül van, és egyszerre mindig csak 1 autó mozog. 1 autó 1 teljes négyzetet foglal el és csak a négyzetrács mentén mozoghatnak függőlegesen vagy vízszintesen.)
|
 |
|
|
| [2635] Róbert Gida | 2008-05-12 01:35:06 |
 Ha valaki ki akarná számolni: Monte Carlo módszere kb. 0.177-et ad az integrálra, 1 millió pontot használva az egységnégyzetből, ez így kb. 1/sqrt(1000000)=1/1000-ed pontosságot jelent.
|
| Előzmény: [2634] Gyöngyő, 2008-05-12 00:58:33 |
|
| [2634] Gyöngyő | 2008-05-12 00:58:33 |
 Mennyi a következő integrál értéke: Ahol a kapcsos zárójel törtrészt jelent:
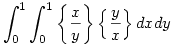
Üdv.: Zsolt
|
|









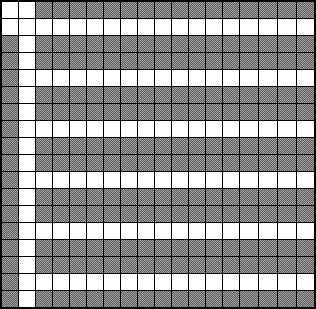
 57,143%. Viszont 6×6-asra tudtam egy kicsit jobbat is csinálni, csak a bal felső (pirosra festett) autót kell kiszedni. De egyetlen autó kivétele nem befolyásolja a határértéket, ami jelen esetben 21/36
57,143%. Viszont 6×6-asra tudtam egy kicsit jobbat is csinálni, csak a bal felső (pirosra festett) autót kell kiszedni. De egyetlen autó kivétele nem befolyásolja a határértéket, ami jelen esetben 21/36
 x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja.
x, akkor megtehetjük azt is, hogy egy (vagu több) közepes négyzetet kis négyzetek közé fáziseltolással csempészünk be, ahogy a második ábra mutatja. 


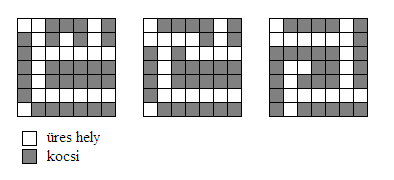

 1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség.
1(modn) azok éppen a prímek és a Carmichael-számok. Prímek esetén viszont van olyan a<n, amely primitív gyök, erre az a-ra nem teljesülhet a feladatban kitűzött egyenlőség. 
 2 gondolom így sokat segít.
2 gondolom így sokat segít.