Előre is bocs, TeX-ben (újra)kezdő vagyok!
Ha bevezetjük az
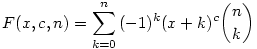
jelölést, akkor az igazolandó állítás: F(0,c,n)=0, ha c<n. Mi egy kicsit általánosabbat fogunk bizonyítani: F(x,c,n) 0 is igaz. 0 is igaz.
Biz.: Indukcióval.(Ha c,n-t rögzítjük, akkor F egyváltozós -csak x!- függvény.) Valamint a továbbiakban feltesszük, hogy n>c mindig.
F(x,1,2)=x-2(x+1)+(x+2) 0, ez rendben. Ezek szerint F(x,1,2) (c,n-t rögzítve) a konstans 0 függvény, és persze -F(x+1,1,2) 0, ez rendben. Ezek szerint F(x,1,2) (c,n-t rögzítve) a konstans 0 függvény, és persze -F(x+1,1,2) 0 is igaz. Ha kirészletezzük 0 is igaz. Ha kirészletezzük
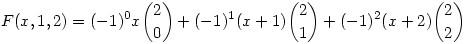
valamint
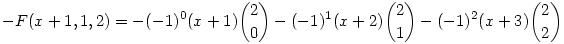
Mivel a binomiális együtthatókra igaz, hogy
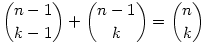
, emiatt 0 F(x,1,2)-F(x+1,1,2)=F(x,1,3) is igaz. (Azért írtam ilyen részletesen, mert az indukció többi lépése ugyanerre az ötletre épül.) F(x,1,2)-F(x+1,1,2)=F(x,1,3) is igaz. (Azért írtam ilyen részletesen, mert az indukció többi lépése ugyanerre az ötletre épül.)
Hasonlóan ha F(x,1,n) 0, akkor -F(x+1,1,n) 0, akkor -F(x+1,1,n) 0 és az előzőek szerint F(x,1,n+1) 0 és az előzőek szerint F(x,1,n+1) 0 is igaz, vagyis c=1-re igaz az állítás. 0 is igaz, vagyis c=1-re igaz az állítás.
Másfelől ha F(x,c,n)-t x- szerint deriváljuk, F'(x,c,n)=cF(x,c-1,n). Emiatt, ha F(x,c,n) 0, akkor F(x,c+1,n) 0, akkor F(x,c+1,n) d valamilyen d számra. Azt kellene látni, hogy feltéve, hogy F(x,n-2,n) d valamilyen d számra. Azt kellene látni, hogy feltéve, hogy F(x,n-2,n) 0, F(x,n-1,n) 0, F(x,n-1,n) d esetén d csak a 0 lehet. Ez pedig a következők miatt igaz: x=-n/2 helyettesítéssel: d esetén d csak a 0 lehet. Ez pedig a következők miatt igaz: x=-n/2 helyettesítéssel:
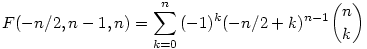
itt n akár páros, akár páratlan az első-utolsó, második-utolsó előtti... tagok a szummában egymás ellentettjei (páros n esetén a középső tag egy 0), így összegük: 0. Mivel F(x,n-1,n) konstans volt, csak a konstans 0 lehet. Ezek szerint F(x,1,3) 0 miatt F(x,2,3) 0 miatt F(x,2,3) 0 is igaz, innen hasonlóan, mint c=1 esetén F(x,2,n) (n>2) is a konstans 0. Onnan F(x,3,4) 0 is igaz, innen hasonlóan, mint c=1 esetén F(x,2,n) (n>2) is a konstans 0. Onnan F(x,3,4) 0, majd F(x,3,n) 0, majd F(x,3,n) 0 (n>3) és így tovább... Ezzel az állítást beláttuk. 0 (n>3) és így tovább... Ezzel az állítást beláttuk.
Melléktermékként kijöttek nekem a következő összefüggések (bizonyítás nélkül):
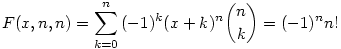
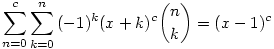
Ez utóbbi két összefüggés (1.) x=0, valamint (2.) x=-1,0,1 esetén szép összegeket ad, valamint a második összegben c-helyett végtelenig is mehetünk.
Feladat: bizonyítsuk ezt a két utóbbi összeget!
Ui.: Bocs ez egy kicsit szószátyár lett. Hellósztok!
|



 z) zárójelezések számát. Ha n kisebb mint z, akkor pn,z=0, ami azt jelenti, hogy kevesebb a nyitó mint a záró zárójel, vagyis a zárójelezés nem folytatható. Ekkor pn,0=1 (n db. nyitó zárójel), és
z) zárójelezések számát. Ha n kisebb mint z, akkor pn,z=0, ami azt jelenti, hogy kevesebb a nyitó mint a záró zárójel, vagyis a zárójelezés nem folytatható. Ekkor pn,0=1 (n db. nyitó zárójel), és 








 0 is igaz.
0 is igaz.