| [268] Csimby | 2004-02-25 11:00:28 |
 Andris mindenképpen eltudja érni, hogy egyenlők legyenek az esélyek, ha az egyik kockára 1,2,3,16,17,18-at ír. Ha Béla nem, akkor ő kiválasztja ezt a kockát -> 1/2 valószínűséggel nyer, függetlenül a másik két kockától.
Tehát ha valakinek van nyerő stratégiája, az Andris. Olyan elosztást kéne találni, hogy az A kocka jobb a B-nél, B a C-nél, C az A-nál -> Béla akármit választ, Andris tud jobbat.
|
|
| [267] lorantfy | 2004-02-25 10:52:45 |
 Kedves Károly és Fórumosok!
Abból, hogy a számok összege minden kockán 57 én még nem látom tisztán, hogy egyenlő lenne a nyerési esély és van ilyen elosztás?
Én igy gondolom: András nyilván igyekszik úgy elosztani a számokat, hogy legalább két kockával egyenlő legyen a nyerési esély és a harmadikkal ezeknél kisebb. Ha ez lehetséges, akkor egyenlő valószinüséggel nyerhetnek. (A 3. kocka azért nem lényeges, mert Béla kiválasztja az egyik jobb kockát, András meg a másikat)
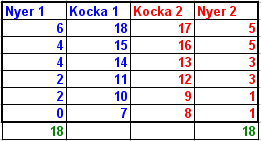
A lenti táblázatba beírtam a számok elosztásását. A szélső oszlopokba pedig, hogy az adott szám hány párban nyerő. A 36 lehetőségből mindkét kocka 18-18 szor nyer. Tehát mindeny, hogy kinek a helyében játszunk
|
 |
| Előzmény: [264] Hajba Károly, 2004-02-24 21:05:58 |
|
| [266] Sirpi | 2004-02-25 10:52:29 |
 Az előző példám nagyon sarkított, és természetesen nem fér bele a feladat kereteibe (1-18-ig terjedő, különböző számok), de rávilágít valamennyire a dologra...
S
|
| Előzmény: [265] Sirpi, 2004-02-25 10:47:37 |
|
| [265] Sirpi | 2004-02-25 10:47:37 |
 Sajnos ez az érvelés hibás... Tegyük fel, hogy van két kockánk, egyiken 0, 0, 0, 0, 0, 100000 számok vannak, a másikon 1,1,1,1,1,1 számok. Melyik kocka a jobb? A másodikkal 5/6 eséllyel nyerek az első ellen, pedig az összeg (átlag) kisebb rajta.
S
(Imserem a megoldást, de csöndben maradok...)
|
| Előzmény: [264] Hajba Károly, 2004-02-24 21:05:58 |
|
| [264] Hajba Károly | 2004-02-24 21:05:58 |
 60. feladathoz:
Ha András úgy ossza ki a számokat a dobókockák között, hogy az egyik kocka oldalösszege nagyobb, mint a többin, akkor Béla ezt választva hosszútávon elönyt élvezhetne, mivel magasabb átlagpontot érne el vele. Amennyiben mindhárom kockán egyenletesen vannak elosztva a számok, azaz egy-egy kockán található számok összege 57-57, teljesen mindegy a választott kockán lévő számok értéke, hosszútávon kiegyenlítődik a játék. A teljesen egyenletes eloszlás miatt úgy kell a kiosztást elvégezni, hogy egy-egy kocka két-két ellentétes oldalán található számok összege 19 legyen.
Ezzel a taktikával mindegy, hogy ki kezd és véletlenszerű a különbség.
HK
|
| Előzmény: [263] Gyuri, 2004-02-23 15:19:09 |
|
| [263] Gyuri | 2004-02-23 15:19:09 |
 Kedves Fórumosok!
Íme egy újabb feladat:
60. feladat: András és Béla játszák a következő játékot: András az 1,2,...,18 számokat felírja 3 db, kezdetben számozatlan dobókocka lapjaira, minden lapra pontosan egy számot. Ezután Béla választ egy kockát e három közül, persze a választás előtt kedvére tanulmányozhatja őket. András a megmaradt két kocka közül választ, majd rátérnek a játék fő részére. Dobnak mindketten a saját kockájukkal, és a nagyobb számot dobó elnyer egy forintot a másiktól. Így dobálgatnak a kockáikkal, minden lépésben a sajátjukkal. Kérdés: kinek a helyében érdemes játszani? mennyire éri meg?
Üdv: Gyuri
|
|
|
|
| [260] Gubbubu | 2004-02-19 20:16:44 |
 Kedves Fórum!
A következő feladatot azoknak ajánlom, akik az itteni versenyszintű feladatokat túl nehéznek, de a "darálós" matematikafeladatokat (pl. zöld könyv) túl könnyűnek érzik.
59. fa.: Oldjuk meg a
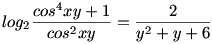
egyenletet, (x,y) R2 R2
|
|
| [259] Lóczi Lajos | 2004-02-19 04:32:18 |
 Kedves Onogur!
Még utoljára hadd reagáljak én is a kérdésre. Persze, én is hasonlóra gondoltam a "képlet" szó hallatán---arra a néhány "önkényesen" kijelölt függvényre (pl. szinusz, logaritmus, négyzetgyök, stb.), melyeket "legtöbbször" használunk, illetve ilyenekből (véges sok lépésben ?) a függvényműveletekkel (pl. alapműveletek, kompozíció, inverz, stb.) készíthető függvényekre.
A "véges lépésben kifejezhetőség" kérdését és a másodfokú egyenlet megoldóképletét nézhetjük azonban a következő nézőpontból is: pl. már az x2=2 (x>0) egyenlet megoldása, azaz 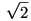 sem fejezhető ki racionális számokkal és véges sok alapművelettel; természetesen a határérték felhasználásával (és végtelen sok racionális szám felhasználásával) már kifejezhető. De ugyanígy van a 10x=2 egyenlet valós megoldásával is: a log102 kifejezést sem lehet a határérték fogalmának mellőzésével véges sok racionális számból megkonstruálni. (Limesz segítségével persze könnyen definiálható pl. a logaritmus hatványsora és így a log102 szám is.) Ugyanez a helyzet tehát minden irracionális számmal, hiszen irracionális számokat "konstruálni" csak már valami meglévő "anyagból", pl. a racionális számokból lehet. sem fejezhető ki racionális számokkal és véges sok alapművelettel; természetesen a határérték felhasználásával (és végtelen sok racionális szám felhasználásával) már kifejezhető. De ugyanígy van a 10x=2 egyenlet valós megoldásával is: a log102 kifejezést sem lehet a határérték fogalmának mellőzésével véges sok racionális számból megkonstruálni. (Limesz segítségével persze könnyen definiálható pl. a logaritmus hatványsora és így a log102 szám is.) Ugyanez a helyzet tehát minden irracionális számmal, hiszen irracionális számokat "konstruálni" csak már valami meglévő "anyagból", pl. a racionális számokból lehet.
Már az is szerencsének számít szerintem, hogy egy "véletlenszerűen" felírt nemlineáris egyenletnek egyáltalán kifejezhető a megoldása a "megszokott", elemi függvények segítségével (és határértékképzéssel).
Ilyen típusú tételekkel, kérdésfelvetéssel egyébként a primitívfüggvény-keresés (azaz határozatlan integrálás) elméletében foglalkoznak, meg lehet kérdezni pl., hogy egy adott függvénynek a (bizonyíthatóan létező) primitív függvénye egy adott függvényosztályban van-e: pl. jól ismert, hogy az x e-x2 függvény primitív függvénye "nem elemi" függvény, azaz a "szokásos" képletekkel nem "fejezhető ki". Ennek ellenére egyszerű hatványsorral (ismét határértékképzés!) minden további nélkül előállítható a primitív függvénye. (És ha tetszik, be is vezethetünk erre egy új nevet, ahogyan ezt szokták is (valójában a függvény konstansszorosát nevezik el): legyen ez az ún. hibafüggvény, és jelöljük az erf(x) jellel. Ezzel aztán ugyanúgy számolhatunk, mint pl. a log(x) függvénnyel...tehát a történetnek sosem lehet vége.) e-x2 függvény primitív függvénye "nem elemi" függvény, azaz a "szokásos" képletekkel nem "fejezhető ki". Ennek ellenére egyszerű hatványsorral (ismét határértékképzés!) minden további nélkül előállítható a primitív függvénye. (És ha tetszik, be is vezethetünk erre egy új nevet, ahogyan ezt szokták is (valójában a függvény konstansszorosát nevezik el): legyen ez az ún. hibafüggvény, és jelöljük az erf(x) jellel. Ezzel aztán ugyanúgy számolhatunk, mint pl. a log(x) függvénnyel...tehát a történetnek sosem lehet vége.)
|
| Előzmény: [258] Hajba Károly, 2004-02-19 00:42:09 |
|
| [258] Hajba Károly | 2004-02-19 00:42:09 |
 Kedves Lajos!
A "pontos érték" alatt én is olyasvalamire gondoltam, mint gubbubu; vagy például képlet alatt olyanra, mint a másodfokú megoldóképlet, tehát véges lépésben kifejezhető érték. Feltehetően nem pontosan fogalmaztunk.
De azt javaslom, hogy ezirányú pontosításokat ne folytassuk, mivel ilyen - fent vázolt módon kifejezhető formában - feltehetően nem létezik, másrészről a feladatot természetesen megoldotnak tekintem én is. :o)
HK
|
| Előzmény: [256] Lóczi Lajos, 2004-02-18 02:53:55 |
|
|
| [256] Lóczi Lajos | 2004-02-18 02:53:55 |
 Kedves Onogur!
Mit értesz pontosan "pontos érték" alatt? Megmutattuk, hogy a harmadik megoldás létezik, egy valós szám, és más, ismert mennyiségekből elő is állítottuk (határérték segítségével).
Üdv, Lajos
|
| Előzmény: [250] Hajba Károly, 2004-02-17 14:18:00 |
|
| [255] Gubbubu | 2004-02-17 20:37:02 |
 Kedves Zormac!
Ha minden igaz, eredetileg az n tényleg egész volt, tehát jól emlékszel (amennyiben én is jól emlékszem). Csak később Onogur és én kutatásokat:-) végeztünk a feladat mindenféle általánosításaival kapcsolatban. Egyébként egy másik (talán a 46.)-os feladatban azt mondtam, hogy a megoldó kedve szerint választhat az N,Z,Q,R,C alaphalmazok közül, és ezek felett is megoldhatja az egyenletet, a probléma bármely variációja más-más okok miatt érdekes lehet.
|
| Előzmény: [241] Zormac, 2004-02-13 14:20:48 |
|
|
| [253] Rizsa | 2004-02-17 15:41:45 |
 Kedves Sirpi!
Hat ez nagyon nem kellett volna az en gyenge idegrendszeremnek, elegge idegbetegnek ereztem eddig is magam, de most hogy negyed ora probalkozas meg magamban uvoltozes utan itt egy gepteremben vegul is sikerult... hat nem mondom, jo erzes, amugy nagyon vicces volt, csak az elindulas tartott 5 percig. minden elismeresem eme remekmu felfedezesehez. levezetoul ajanlom a kovetkezot: laget.kicks-ass.net/pingvin/ kivalo mulatsag, egy kicsit kevesebb szellemi szint igenyevel.
udv, rizs
|
| Előzmény: [249] Sirpi, 2004-02-17 13:12:19 |
|
| [252] Hajba Károly | 2004-02-17 14:36:34 |
 Kedves László!
Úgy tűnik, hogy szilveszter óta senki sem tért még magához :o), mivel a 44. feladatra még nem jött megoldás. Én is csak részmegoldást tudok adni, mivel csak a bikákra jött ki egész érték. Tehát a csordában 2226 fehér, 1602 fekete, 1580 tarka és 891 barna bika van, vagy együttesen egész számú többszörösei. A tehenekre eddig csak túl magas szám jött ki az egész számok körében.
HK
|
| Előzmény: [199] lorantfy, 2003-12-29 14:48:13 |
|
| [251] Hajba Károly | 2004-02-17 14:21:24 |
 Kedves zormac!
Eredetileg a kéttagú szorzatokra gondoltam, így meglelted a 9 megoldást. A többtagú szorzattal nem foglalkoztam, de érdekes a kiegészítésed. Köszönet érte.
HK
|
| Előzmény: [247] Zormac, 2004-02-17 12:28:57 |
|
| [250] Hajba Károly | 2004-02-17 14:18:00 |
 Kedves Sirpi!
Valószínű, hogy én kavartam be egy kicsit, de a [215] alatt gubbubu feltette a következő kiegészítő kérdését:
48.C. feladat: Nincs-e a harmadik, nem egész megoldásnak pontos értéke, mondjuk valami egész szám logaritmusa?
Erre eddig nem jött az iteratív válaszon kivül más. Tehát még annyi sem egy igazi matematikustól, hogy ... Ne is keressétek, mivel jelenleg nem tud a matematika ilyent felállítani! vagy bizonyítás, hogy nem lehet ilyent felállítani. Itt most nem LL határértékszámítási képletére gondolok.
HK
|
| Előzmény: [249] Sirpi, 2004-02-17 13:12:19 |
|
| [249] Sirpi | 2004-02-17 13:12:19 |
 Ja, és Csimby, bocs, hogy ugyanazt mondtam el, mint Te, de mivel azt írta itt valaki, hogy még nem oldódott meg a 47. példa, söt, Zormac is írt rá egy megoldást, ezért nem álltam neki utánanézni, hogy tényleg meg lett-e már oldva. Bocsi érte.
S
|
| Előzmény: [245] Csimby, 2004-02-16 20:12:00 |
|
| [248] Sirpi | 2004-02-17 12:45:11 |
 Sziasztok!
Akinek anno tetszett a farkas, kecske, káposzta folyón való átvitele, de túl könnyünek találta, annak itt egy kicsit nehezebb változat:
A nagy japán folyós játék
Sajna a szöveg japánul van, de ez ne riasszon el senkit, a kezdöképernyön a nagy kerek gombra kell bökni, és utána át kell juttatni az anyukát, apukát, két lányukat, két fiukat, valamint a rendört és a fegyencet a túlpartra, a következök figyelembevételével:
- Mindenkinek át kell menni a folyón
- Csak két személy lehet egyszerre a tutajon
- Az apa nem maradhat egyedül egyik lánnyal sem mert megveri ot
- Az anya nem maradhat egyedül egyik fiúval sem mert megveri ot
- A fegyenc (csíkos ruha) nem maradhat a rendor felügyelete nélkül mert megver valakit
- Csak az anya, az apa és a rendor vezetheti a tutajt
- A fegyenc egyedül maradhat, nem fog megszökni
Jó szórakozást a játékhoz!
S
|
|
| [247] Zormac | 2004-02-17 12:28:57 |
 57. feladathoz
Nem tudom, vajon van-e ennek a feladatnak elemi megoldása, s mivel én nem találtam olyat, így programmal estem neki. Ha már lúd, legyen kövér: nem csak a kitűzött formátumú megoldásokat kerestem, hanem másokat is, amelyek ráillenek a kiírás szövegére. Az eredeti, vagyis az AB*CDE=GHIJ formátumból az alábbi hetet találta a progi:
12 x 483 = 5796; 18 x 297 = 5346; 27 x 198 = 5346; 28 x 157 = 4396; 39 x 186 = 7254; 42 x 138 = 5796; 48 x 159 = 7632
Emellett adódott két darab A*BCDE=GHIJ típusú megoldás (4 x 1738 = 6952; 4 x 1963 = 7852), valamint számtalan A*B*CDE=GHIJ és A*BC*DE=GHIJ típusú is, például 3 x 28 x 71 = 5964 illetve 6 x 9 x 138 = 7452.
A négyféle típus elemeinek összlétszáma 79.
Akit esetleg érdekel, a program forrása és teljes kimenete megtalálható itt.
|
| Előzmény: [246] Hajba Károly, 2004-02-16 22:43:09 |
|
| [246] Hajba Károly | 2004-02-16 22:43:09 |
 57. feladat:
Tekintsük a 48×159=7632 szorzatot, melyben az 1-9 számjegyek mindegyike szerepel, de csak egyszer. Képezzünk hasonló szorzásokat!
HK
|
|
| [245] Csimby | 2004-02-16 20:12:00 |
 Én is ezt mondtam [216]-ban, de hát gyorsan felejtenek a népek...
|
|
| [244] Sirpi | 2004-02-16 11:07:28 |
 n2+1=2m és m 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás. 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.
m=0 esetén n=0, m=1 esetén n= 1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk. 1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk.
S
|
| Előzmény: [238] Zormac, 2004-02-12 16:24:18 |
|









 R2
R2 
 e-x2 függvény primitív függvénye "nem elemi" függvény, azaz a "szokásos" képletekkel nem "fejezhető ki". Ennek ellenére egyszerű hatványsorral (ismét határértékképzés!) minden további nélkül előállítható a primitív függvénye. (És ha tetszik, be is vezethetünk erre egy új nevet, ahogyan ezt szokták is (valójában a függvény konstansszorosát nevezik el): legyen ez az ún. hibafüggvény, és jelöljük az erf(x) jellel. Ezzel aztán ugyanúgy számolhatunk, mint pl. a log(x) függvénnyel...tehát a történetnek sosem lehet vége.)
e-x2 függvény primitív függvénye "nem elemi" függvény, azaz a "szokásos" képletekkel nem "fejezhető ki". Ennek ellenére egyszerű hatványsorral (ismét határértékképzés!) minden további nélkül előállítható a primitív függvénye. (És ha tetszik, be is vezethetünk erre egy új nevet, ahogyan ezt szokták is (valójában a függvény konstansszorosát nevezik el): legyen ez az ún. hibafüggvény, és jelöljük az erf(x) jellel. Ezzel aztán ugyanúgy számolhatunk, mint pl. a log(x) függvénnyel...tehát a történetnek sosem lehet vége.) 

 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.
2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.  1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk.
1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk.