|
|
| [2707] Python | 2008-06-29 20:05:28 |
 Egy 2x2 méteres négyzet alakú papírlap mögött el van rejtve egy 1 méter átmérőjű kör alakú céltábla. Legalább hányszor kell rálőnie egy mindig pontosan célzó mesterlövésznek, hogy biztosan eltalálja a céltáblát? (A találatok pontszerűek, a céltábla pereme is érvényes találat.)
|
|
| [2706] jenei.attila | 2008-06-27 22:15:49 |
 Nagyon szép. Máris találtunk 3 látszólag teljesen különböző rekurziót. Mepróbáltam a teljes indukciós bizonyítást, egyelőre nem sokra jutottam vele, de még nem adtam fel. Azért nem könnyű. Kiváncsi lennék egy közvetlen kombinatorikai gondolatmenetre, ami egyből kiadja a zárt alakot.
|
| Előzmény: [2705] leni536, 2008-06-27 18:43:15 |
|
| [2705] leni536 | 2008-06-27 18:43:15 |
 Legyen n db nyitó és n db záró zárójelünk. A helyes zárójelezések száma an.
a0=1
Vizsgáljuk meg, hogy n+1 db nyitó és záró zárójelből hány zárójelezés készíthető. A zárójelezés nyilván egy nyitó zárójellel kezdődik, ennek keressük meg a záró párját. A kettő között elhelyezkedik k db zárójelpár, utána pedig n-k:
( k db zárójelpár ) n-k db zárójelpár
A két zárójel között ak, utána pedig an-k zárójelezés készíthető. Mivel k 0-tól n-ig terjedhet, ezért:
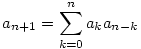
Sirpi Wikipédiás linkje alapján ezek egyértelműen a Catalan számok.
|
|
| [2704] Sirpi | 2008-06-27 13:47:57 |
 Egyébként ezt az angol nyelvű linket is érdemes megnézni, itt 3 különböző bizonyítás is van a dologra (egy generátorfüggvényes és két elemi - utóbbinak külön szépsége, hogy az  szorzót is megmagyarázza), zárójelezés helyett jobbra és felfelé lépkedő, főátló alá nem lépő királlyal. szorzót is megmagyarázza), zárójelezés helyett jobbra és felfelé lépkedő, főátló alá nem lépő királlyal.
|
| Előzmény: [2703] lorantfy, 2008-06-27 11:05:36 |
|
|
|
| [2701] jenei.attila | 2008-06-25 14:53:42 |
 A pn,z-re (ha n z) nem tudok zárt képletet, de pn,n másképp is felírható, ami alapján egy teljes indukciós bizonyítás sikerre kell hogy vezessen. Az összes zárójelezések száma z) nem tudok zárt képletet, de pn,n másképp is felírható, ami alapján egy teljes indukciós bizonyítás sikerre kell hogy vezessen. Az összes zárójelezések száma 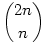 , amiből ki fogjuk vonni a rossz zárójelezések számát. Vezessünk be egy s számlálót 0 kezdőértékkel, amely a zárójelekből álló sztringet elejétől olvasva 1-gyel nő, ha nyitó, illetve 1-gyel csökken, ha záró zárójelet olvasunk. A zárójelezés nyilván akkor romlik el, amikor az s -1 -et vesz fel, ez pedig csak páratlan pozícióban lehet. Pl. nyilván rossz a zárójelezés, ha )-lel kezdődik. Tehát a következőképpen számolunk: A szóban forgó páratlan pozíció (2i+1) előtt befejezett, jó zárójelezés áll (s=0), aztán záró zárójel következik. Ezen esetek száma az előző 2i pozíción létrejövő jó zárójelezések száma (pi,i), szorozva a 2i+2 -edik pozíciótól kezdődő összes zárójelezések számával ( , amiből ki fogjuk vonni a rossz zárójelezések számát. Vezessünk be egy s számlálót 0 kezdőértékkel, amely a zárójelekből álló sztringet elejétől olvasva 1-gyel nő, ha nyitó, illetve 1-gyel csökken, ha záró zárójelet olvasunk. A zárójelezés nyilván akkor romlik el, amikor az s -1 -et vesz fel, ez pedig csak páratlan pozícióban lehet. Pl. nyilván rossz a zárójelezés, ha )-lel kezdődik. Tehát a következőképpen számolunk: A szóban forgó páratlan pozíció (2i+1) előtt befejezett, jó zárójelezés áll (s=0), aztán záró zárójel következik. Ezen esetek száma az előző 2i pozíción létrejövő jó zárójelezések száma (pi,i), szorozva a 2i+2 -edik pozíciótól kezdődő összes zárójelezések számával (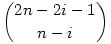 ). Ha i megy 0-tól n-1 -ig, ezek összege megadja az összes rossz zárójelezést. Vagyis: ). Ha i megy 0-tól n-1 -ig, ezek összege megadja az összes rossz zárójelezést. Vagyis:
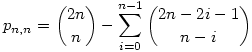
Ebben a rekurzióban már csak egy index szerepel, úgyhogy teljes indukcióval bebizonyítható, hogy a Catalan számokat adja. Sok sikert.
|
| Előzmény: [2700] lorantfy, 2008-06-24 10:55:29 |
|
|
|
|
| [2697] jenei.attila | 2008-06-23 13:03:50 |
 Nem tudom beszúrni a linket. E téma 80. oldal, 685 hsz.
Link javítva - Sirpi
|
|
| [2698] jenei.attila | 2008-06-23 12:36:36 |
 Jelöljük pn,z-vel, az n db. nyitó és z db. záró zárójelből álló "folytatható" (n z) zárójelezések számát. Ha n kisebb mint z, akkor pn,z=0, ami azt jelenti, hogy kevesebb a nyitó mint a záró zárójel, vagyis a zárójelezés nem folytatható. Ekkor pn,0=1 (n db. nyitó zárójel), és z) zárójelezések számát. Ha n kisebb mint z, akkor pn,z=0, ami azt jelenti, hogy kevesebb a nyitó mint a záró zárójel, vagyis a zárójelezés nem folytatható. Ekkor pn,0=1 (n db. nyitó zárójel), és
pn,z=pn,z-1+pn-1,z
megfelelően annak, hogy egy n nyitó és z-1 záró zárójelből álló, vagy egy n-1 nyitó és z záró zárójelből alló folytatható zárójelezést folytatunk nyitó, illetve záró zárójellel.
A feladat, nyilván a pn,n értékét kérdezi, amire az első néhány értéket kiszámolva:
p1,1=1,p2,2=2,p3,3=5,p4,4=14,p5,5=42
.
Zárt alakot nem sikerült találni, de egyébként a feladat tulajdonképpen azonos Atos gyógyszeres feladatával, amire szintén nem találtunk zárt alakot annak idején.
|
| Előzmény: [2693] lorantfy, 2008-06-20 10:50:43 |
|
|
| [2693] lorantfy | 2008-06-20 10:50:43 |
 Van n db zárójelünk, fele nyitó fele záró. Hány féle helyes zárójelezést lehet ezekkel megvalósítani?
|
|
|
|
| [2690] Róbert Gida | 2008-06-10 18:34:59 |
 Azt azért hozzátehetted volna, hogy a pontonkénti konvergenciát láttad be. A kérdés is egy kicsit gagyi volt, csak úgy, hogy konvergens nem mondjuk a függvényekre, szerintem. Továbbá azt sem árt megjegyezni, hogy az fn függvények nem ugyanazon az intervallumon vannak értelmezve...
Az egyenletes konvergencia már nem igaz.
|
| Előzmény: [2686] leni536, 2008-06-09 18:12:37 |
|
| [2689] leni536 | 2008-06-10 14:15:46 |
 Az an (bn) sorozat monoton növekvő (csökkenö) és felső (alsó) korlátja f(x). Ugyanis az n+1. intervallum részhalmaza az n. intervallumnak, ezért a fügvény minimuma (maximuma) az intervallumon nem csökkenhet (nőhet).
|
| Előzmény: [2687] nadorp, 2008-06-10 08:56:14 |
|
|
| [2687] nadorp | 2008-06-10 08:56:14 |
 A befejezés egy kicsit hiányos.
"A folytonosság úgy teljesülhet, ha: ...", helyett az kéne, hogy
Mivel az f(x) függvény folytonos, ezért ....
De honnan tudjuk, hogy az an,bn sorozatok konvergensek, miért következik ez a folytonosságból ?
|
| Előzmény: [2686] leni536, 2008-06-09 18:12:37 |
|
| [2686] leni536 | 2008-06-09 18:12:37 |
 Legyen an a függvény minimuma, bn a függvény maximuma az ![\left[x-\frac1n,x+\frac1n\right]](keplet.cgi?k=47741834DE2AA290) intervallumon. intervallumon.

(Két függvényt integrálunk és az egyik minden pontban nagyobb vagy egyenlő, mint a másik)
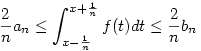
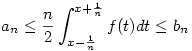
A folytonosság úgy teljesülhet, ha:
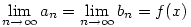
A rendőrelv alapján a keresett határérték:
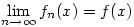
|
| Előzmény: [2685] Gyöngyő, 2008-06-09 17:01:17 |
|
| [2685] Gyöngyő | 2008-06-09 17:01:17 |
 Sziasztok!
Van egy jó kis feladatom!
Legyen f folytonos (0,1)-en. Konvergens-e a következő függvénysorozat?
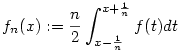
bocs, de a képletbeírási megoldásod "enyhén" rontotta a fórumképet, javítottam - Sirpi
|
|
| [2684] lgdt | 2008-06-09 00:24:52 |
 Hű, érdekes megoldások. Mi egy polinomos feladat kapcsán jöttünk rá, hogy ez így van.
Vegyük egy tetszőleges c-edfokú polinomfüggvény helyettesítési értékeit n+1 egymást követő egész helyen: P(x),P(x+1),...,P(x+n), legyen c<n.
Vonjuk ki az értékekből az őket megelőző értékeket (azaz képezzük a differencia-sorozatot), ekkor egy kisebb fokszámú polinomfüggvény helyettesítési értékeit kapjuk eggyel kevesebb helyen (vagy ha konstans 0 volt, akkor konstans 0-t).
Ezt n-szer ismételve egyetlen szám marad. Kövessük nyomon, hogy ez az első polinom helyettesítési értékeitől hogyan függ: látjuk, hogy mivel a képzési szabály éppen a váltakozó előjelekkel megtűzdelt Pascal-háromszög képzési szabálya, ezt kapjuk:
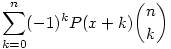
Ekkorra a polinom már teljesen elfogy, ezért a megmaradó szám csak 0 lehet.
Írok egy példát is:
| a, b, c, d, e // harmadfokú |
| b-a, c-b, d-c, e-d // másodfok |
| c-2b+a, d-2c+b, e-2d+c // elsőfokú |
| d-3c+3b-a, e-3d+3c-b // nulladfokú |
| e-4d+6c-4b+a = 0 |
|
Azért nagyon jó ez az egész, mert könnyen meg lehet vele mondani egy polinom következő helyettesítési értékét az előzőek alapján.
Arra vagyok nagyon kíváncsi, hogy van-e kombinatorikai interpretációja a feladatnak, és esetleg van-e kombinatorikai megoldása.
|
|








 z) nem tudok zárt képletet, de pn,n másképp is felírható, ami alapján egy teljes indukciós bizonyítás sikerre kell hogy vezessen. Az összes zárójelezések száma
z) nem tudok zárt képletet, de pn,n másképp is felírható, ami alapján egy teljes indukciós bizonyítás sikerre kell hogy vezessen. Az összes zárójelezések száma  z) zárójelezések számát. Ha n kisebb mint z, akkor pn,z=0, ami azt jelenti, hogy kevesebb a nyitó mint a záró zárójel, vagyis a zárójelezés nem folytatható. Ekkor pn,0=1 (n db. nyitó zárójel), és
z) zárójelezések számát. Ha n kisebb mint z, akkor pn,z=0, ami azt jelenti, hogy kevesebb a nyitó mint a záró zárójel, vagyis a zárójelezés nem folytatható. Ekkor pn,0=1 (n db. nyitó zárójel), és 




