| [2721] Gyöngyő | 2008-07-24 08:01:03 |
 Sziasztok!
Kit érdekelne esetleg egy pár db könyv(angolul),pdf fájlban? 8gb anyag körülbelül 3500db könyvem van,és jobbnál jobb témák,pl: Ramanujan könyvek. Akit érdekel bátran irjon!
Üdv.: Zsolt
|
|
| [2720] szbela | 2008-07-16 21:31:38 |
 Sziasztok!
Először is elnézést a hanyag TEX miatt. Egy picit másképpen Cckek feladatának megoldása:
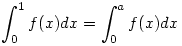
mert 
Legyen g(x):=f(x)/s , ahol s:=sup{|f'(x)|,x [0,1]} [0,1]}
ekkor nyilván sup{|g'(x)|,x [0,1]}=1 [0,1]}=1
Azt kell belátnunk, hogy 
Megmutatjuk, hogy |g(x)|<=a-x+|g(a)|  x x [0,a]-ra [0,a]-ra
Tfh indirekten, hogy  y y [0,a] melyre |g(y)|>a-y+|g(a)| [0,a] melyre |g(y)|>a-y+|g(a)|
ha a=y, akkor nyilvánvalóan ellentmondásra jutunk, ha a y akkor átrendezés után y akkor átrendezés után 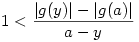
Alkalmazzuk a háromszögegyenlőtlenséget és mivel a>y, így: 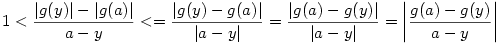 Amire alkalmazva Lagrange-középértéktételét, adódna hogy Amire alkalmazva Lagrange-középértéktételét, adódna hogy  z z (y,a) melyre |g'(z)|>1 Ellentmondásra jutottunk. (y,a) melyre |g'(z)|>1 Ellentmondásra jutottunk.
Beláttuk tehát, hogy |g(x)|<=a-x+|g(a)|  x x [0,a]-ra [0,a]-ra
Alkalmazzuk, hogy 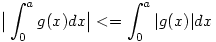 Mivel |g(x)|-et majorálja a-x+|g(a)| [0,a]-n, ezért Mivel |g(x)|-et majorálja a-x+|g(a)| [0,a]-n, ezért 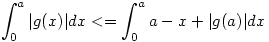 és így elég megmutatnunk, hogy és így elég megmutatnunk, hogy 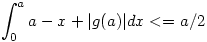 Alkalmazva a Newton-Leibniz-tételt: Alkalmazva a Newton-Leibniz-tételt: 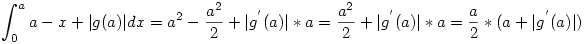
Így most már csak azt kell megmutatni, hogy |g'(a)|<=1-a
Alkalmazva az integrálszámítás középértéktételét  s s [a,1] [a,1] 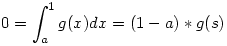 Ebből következik, hogy g(s)=0, hiszen a Ebből következik, hogy g(s)=0, hiszen a 1 1

ismét alkalmazva Lagrange középértéktételét adódik, hogy van ilyen z (a,s) (a,s)
|g'(z)|*|a-s|<=|a-s|=s-a hiszen s>a, s<=1. Amiből adódik, hogy |g'(a)|<=1-a
Így bebizonyítottuk az állítást.
|
| Előzmény: [2711] HoA, 2008-07-08 17:35:00 |
|
| [2719] Gyöngyő | 2008-07-14 17:02:45 |
 Akkor itt egy másik:
Bizonyítsuk be,hogy
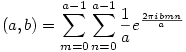
|
|
| [2718] jenei.attila | 2008-07-14 11:32:57 |
 A sorozatot kicsit elszámoltam: 1,2,4,3,6,10,12,4,8,18,...
|
| Előzmény: [2717] jenei.attila, 2008-07-14 11:17:24 |
|
| [2717] jenei.attila | 2008-07-14 11:17:24 |
 Tisztázva az eddigieket: a 2m -1 (mod 2n-1) kongruencia természetesen előállhat, de ez nem jelenti azt, hogy a bal oldali oszlop teljesen fekete lesz. A zavart az okozza, hogy ha 2m -1 (mod 2n-1) kongruencia természetesen előállhat, de ez nem jelenti azt, hogy a bal oldali oszlop teljesen fekete lesz. A zavart az okozza, hogy ha 2m 0 (mod 2n-1), az jelentheti a 2n-1 sorszámú korongot is. A kezdetben 0 (bal alsó) illetve 2n-1 (jobb felső) sorszámú korongok minden művelet után eredeti helyükre térnek vissza, ezért elég a többi korong mozgását követni. Ha 2m 0 (mod 2n-1), az jelentheti a 2n-1 sorszámú korongot is. A kezdetben 0 (bal alsó) illetve 2n-1 (jobb felső) sorszámú korongok minden művelet után eredeti helyükre térnek vissza, ezért elég a többi korong mozgását követni. Ha 2m q (mod 2n-1) (a jobb alsó korong m művelet után a q pozícióba kerül) és 2 q (mod 2n-1) (a jobb alsó korong m művelet után a q pozícióba kerül) és 2 q q 2n-2, akkor könnyen látható, hogy van olyan páros p (2 2n-2, akkor könnyen látható, hogy van olyan páros p (2 p p 2n-2), amelyre qp mod 2n-1 páratlan. Ez azt jelenti, hogy a kezdetben páros p sorszámú korong (bal oszlopbeli fehér) páratlan pozícióba, azaz a jobboldali oszlopba kerül. Márpedig a jobboldali oszlop soha nem lehet teljesen fehér, mivel a tetején mindig fekete korong áll. Vagyis m művelet elvégzése után csak akkor lesznek újra egyszínűek az oszlopok (és ekkor minden korong az eredeti helyére kerül vissza), ha 2m 2n-2), amelyre qp mod 2n-1 páratlan. Ez azt jelenti, hogy a kezdetben páros p sorszámú korong (bal oszlopbeli fehér) páratlan pozícióba, azaz a jobboldali oszlopba kerül. Márpedig a jobboldali oszlop soha nem lehet teljesen fehér, mivel a tetején mindig fekete korong áll. Vagyis m művelet elvégzése után csak akkor lesznek újra egyszínűek az oszlopok (és ekkor minden korong az eredeti helyére kerül vissza), ha 2m 1 (mod 2n-1). 1 (mod 2n-1).
Ha 2m q (mod 2n-1) és 2 q (mod 2n-1) és 2 q q 2n-2 akkor p legyen 2n-1/q felső egészrésze, vagy ha ez páratlan adjunk még hozzá 1-et. Ezzel a p-vel qp páros és 2n 2n-2 akkor p legyen 2n-1/q felső egészrésze, vagy ha ez páratlan adjunk még hozzá 1-et. Ezzel a p-vel qp páros és 2n qp qp 4n-3, vagyis qp mod 2n-1 =qp-(2n-1), ami páratlan. 4n-3, vagyis qp mod 2n-1 =qp-(2n-1), ami páratlan.
Összefoglalva: an olyan, hogy 2an 1 (mod 2n-1). an néhány első értéke: 1,2,4,6,6,10,12,8 1 (mod 2n-1). an néhány első értéke: 1,2,4,6,6,10,12,8
|
| Előzmény: [2713] jenei.attila, 2008-07-12 17:05:19 |
|
|
| [2715] Róbert Gida | 2008-07-13 16:30:11 |
 Mértani sor összegképletét használva az állítás átírható a következő szintén érdekes alakra:
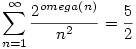
Ahol omega(n) az n különböző prímosztóinak a száma. Bár nem tudom, hogy ez segít a bizonyításhoz...
|
| Előzmény: [2714] Gyöngyő, 2008-07-13 04:19:57 |
|
| [2714] Gyöngyő | 2008-07-13 04:19:57 |
 Bizonyítsuk be,hogy
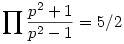
ahol p végig fut a primek halmazán.
|
|
| [2713] jenei.attila | 2008-07-12 17:05:19 |
 Javítás: "1 vagy -1 2-es alapú logaritmusa modulo 2n+1" helyesen: 1 vagy -1 2-es alapú logaritmusa modulo 2n-1. Másrészt a 2m -1 (mod 2n-1) kongruencia valószínűleg soha nem állhat elő, mert a 0 sorszámú korong mindig helyben marad, vagyis a baloldali oszlop soha nem lehet teljesen fekete, márpedig ebből a kongruenciából az következne. Ezen még gondolkozok. -1 (mod 2n-1) kongruencia valószínűleg soha nem állhat elő, mert a 0 sorszámú korong mindig helyben marad, vagyis a baloldali oszlop soha nem lehet teljesen fekete, márpedig ebből a kongruenciából az következne. Ezen még gondolkozok.
|
| Előzmény: [2712] jenei.attila, 2008-07-12 15:49:09 |
|
| [2712] jenei.attila | 2008-07-12 15:49:09 |
 Lórántfy zsetonos feladatáról néhány gondolat. Számozzuk a zsetonokat a következőképen: A baloldali oszlop alsó korongja 0, a jobboldali oszlop alsó korongja 1, a bal oszlop alulról második korongja 2, a jobb oszlop alulról második korongja 3, s.í.t. sorszámokat kapnak. Vagyis a bal oszlopban alulról számolva 0-tól 2n-2 -ig páros sorszámot kapnak, míg a jobboldali oszlopban 1-től 2n-1 -ig páratlan sorszámot kapnak a korongok. összefésülés után, nyilván alulról 0-tól 2n-1 -ig lesznek megszámozva a korongok az egyesített oszlopban. Felezzük el az összefésült oszlopot lórántfy utasítása szerint, majd számozzuk újra a korongokat az előző eljárás szerint. Ekkor, ha egy korong sorszáma eredetileg p volt, akkor újraszámozás után ugyanez a korong 2p mod 2n-1 sorszámot kap. Ha pl. n=3 és a 3-as sorszámú korongot tekintjük (jobboldali oszlop alulról második korongja), akkor ez a 2*3=1 (mod 5) sorszámot kapja, ami azt jelenti, hogy a művelet elvégzése után a jobboldali oszlop aljára kerül. Általában m művelet elvégzése után az eredetileg p sorszámú korong a 2mp mod 2n-1 sorszámot kapja. Látható, hogy így minden egyes korong mozgását pontosan nyomon tudjuk követni. Tekintsük az eredetileg 1-es sorszámú (jobb oszlop alsó) korongot. Ha 2m 1 (mod 2n-1), akkor m menet után ez a korong az eredeti helyére ér vissza. De ekkor minden korong is az eredeti helyére ér vissza, mert nyilván 2mp 1 (mod 2n-1), akkor m menet után ez a korong az eredeti helyére ér vissza. De ekkor minden korong is az eredeti helyére ér vissza, mert nyilván 2mp p (mod 2n-1) is igaz. Ha 2m p (mod 2n-1) is igaz. Ha 2m -1 -1 2n-2 (mod 2n-1), akkor az eredetileg jobb oszlop alsó korongja a bal oszlop tetejére érkezik, és mindkét oszlop oszloponként egyszínű korongokból fog állni, csak éppen az eredeti sorrend fordítottjaként. Tehát a válasz: ha 2m 2n-2 (mod 2n-1), akkor az eredetileg jobb oszlop alsó korongja a bal oszlop tetejére érkezik, és mindkét oszlop oszloponként egyszínű korongokból fog állni, csak éppen az eredeti sorrend fordítottjaként. Tehát a válasz: ha 2m  1 (mod 2n-1), akkor m művelet elvégzése után biztosan újra egyszínű oszlopokat kapunk. Próbálgatással úgy tűnik azonban, hogy kevesebb lépésben ez nem áll elő. Ezt még be kéne bizonyítani. természetesen az m többszörösei is jók, tehát a legkissebb ilyen m-et keressük (1 vagy -1 2-es alapú logaritmusa modulo 2n+1; nem tudom hogy lehet könnyen kiszámítani). 1 (mod 2n-1), akkor m művelet elvégzése után biztosan újra egyszínű oszlopokat kapunk. Próbálgatással úgy tűnik azonban, hogy kevesebb lépésben ez nem áll elő. Ezt még be kéne bizonyítani. természetesen az m többszörösei is jók, tehát a legkissebb ilyen m-et keressük (1 vagy -1 2-es alapú logaritmusa modulo 2n+1; nem tudom hogy lehet könnyen kiszámítani).
|
| Előzmény: [2694] lorantfy, 2008-06-20 11:10:20 |
|
| [2711] HoA | 2008-07-08 17:35:00 |
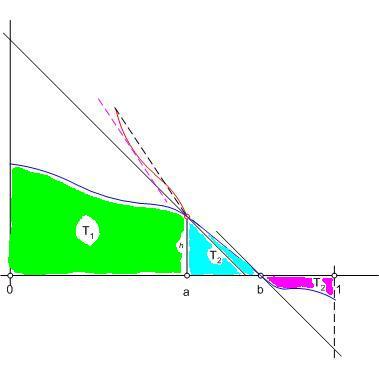
 Amíg nem születik prcíz megoldás, itt egy geomatriai megközelítés, ahol elfogadjuk, hogy "határozott integrál" = "görbe alatti terület" és f'(x) = "érintő meredeksége". A feltétel miatt
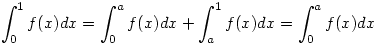
Legyen s=sup{|f'(x)|:x [0,1]}>0 ( a triviális 0 esettől eltekinthetünk ). Mindkét oldalt s-sel osztva a baloldalon g(x) = 1/s f(x) integrálja szerepel, a jobboldalon a/2 . Bizonyítandó tehát: [0,1]}>0 ( a triviális 0 esettől eltekinthetünk ). Mindkét oldalt s-sel osztva a baloldalon g(x) = 1/s f(x) integrálja szerepel, a jobboldalon a/2 . Bizonyítandó tehát:
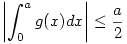 , ,
ahol g olyan függvény, melyre sup{|g'(x)|:x [0,1]}=1 . Tegyük fel, hogy g(a)=h [0,1]}=1 . Tegyük fel, hogy g(a)=h 0 ( ellenkező esetben az abszolút érték miatt vehetjük a -g(x) függvényt ) Ha ábrázoljuk g(x)-et, megállapíthatjuk, hogy 0 és a között nem lehet pontja a -1 meredekségű y = h - ( x - a ) = h + a - x egyenes felett, ugyanis ha valamilyen u-ban g(x) > h + a - u , akkor u és a között lenne olyan v, ahol |g'(v)| > 1. Ugyanígy nem lehet g(x)-nek pontja (0,a) -ban az y = h + x - a egyenes alatt sem. A baloldali integrál abszolut értéke, a görbe alatti terület akkor a legnagyobb, ha a teljes rendelkezésre álló pozitív tartományt kitölti, vagyis 0 ( ellenkező esetben az abszolút érték miatt vehetjük a -g(x) függvényt ) Ha ábrázoljuk g(x)-et, megállapíthatjuk, hogy 0 és a között nem lehet pontja a -1 meredekségű y = h - ( x - a ) = h + a - x egyenes felett, ugyanis ha valamilyen u-ban g(x) > h + a - u , akkor u és a között lenne olyan v, ahol |g'(v)| > 1. Ugyanígy nem lehet g(x)-nek pontja (0,a) -ban az y = h + x - a egyenes alatt sem. A baloldali integrál abszolut értéke, a görbe alatti terület akkor a legnagyobb, ha a teljes rendelkezésre álló pozitív tartományt kitölti, vagyis 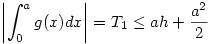 . a és 1 között a görbe alatti terület 0, tehát g(x) negatív értéket is felvesz, ezért van olyan x . a és 1 között a görbe alatti terület 0, tehát g(x) negatív értéket is felvesz, ezért van olyan x (a,1) , ahol g(x) = 0 . Az a-hoz legközelebbi ilyen x legyen b. Az előzőekhez hasonlóan belátható, hogy a és b között a görbének nem lehet pontja az y = h + a - x egyenes alatt, így b (a,1) , ahol g(x) = 0 . Az a-hoz legközelebbi ilyen x legyen b. Az előzőekhez hasonlóan belátható, hogy a és b között a görbének nem lehet pontja az y = h + a - x egyenes alatt, így b a+h és a+h és 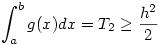 Végül a (b,1) szakaszon Végül a (b,1) szakaszon 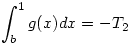 , a görbének nem lehet pontja az y = b -x egyenes alatt, amiből az előzőekhez hasonlóan , a görbének nem lehet pontja az y = b -x egyenes alatt, amiből az előzőekhez hasonlóan  következik. Egyenlőtlenségeinket egybevetve következik. Egyenlőtlenségeinket egybevetve
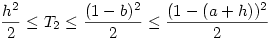 . Nemnegatív számokról lévén szó . Nemnegatív számokról lévén szó 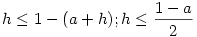
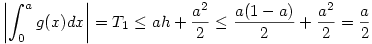
|
 |
| Előzmény: [2710] Cckek, 2008-07-04 10:43:05 |
|
|
|
|
| [2707] Python | 2008-06-29 20:05:28 |
 Egy 2x2 méteres négyzet alakú papírlap mögött el van rejtve egy 1 méter átmérőjű kör alakú céltábla. Legalább hányszor kell rálőnie egy mindig pontosan célzó mesterlövésznek, hogy biztosan eltalálja a céltáblát? (A találatok pontszerűek, a céltábla pereme is érvényes találat.)
|
|
| [2706] jenei.attila | 2008-06-27 22:15:49 |
 Nagyon szép. Máris találtunk 3 látszólag teljesen különböző rekurziót. Mepróbáltam a teljes indukciós bizonyítást, egyelőre nem sokra jutottam vele, de még nem adtam fel. Azért nem könnyű. Kiváncsi lennék egy közvetlen kombinatorikai gondolatmenetre, ami egyből kiadja a zárt alakot.
|
| Előzmény: [2705] leni536, 2008-06-27 18:43:15 |
|
| [2705] leni536 | 2008-06-27 18:43:15 |
 Legyen n db nyitó és n db záró zárójelünk. A helyes zárójelezések száma an.
a0=1
Vizsgáljuk meg, hogy n+1 db nyitó és záró zárójelből hány zárójelezés készíthető. A zárójelezés nyilván egy nyitó zárójellel kezdődik, ennek keressük meg a záró párját. A kettő között elhelyezkedik k db zárójelpár, utána pedig n-k:
( k db zárójelpár ) n-k db zárójelpár
A két zárójel között ak, utána pedig an-k zárójelezés készíthető. Mivel k 0-tól n-ig terjedhet, ezért:
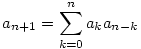
Sirpi Wikipédiás linkje alapján ezek egyértelműen a Catalan számok.
|
|
| [2704] Sirpi | 2008-06-27 13:47:57 |
 Egyébként ezt az angol nyelvű linket is érdemes megnézni, itt 3 különböző bizonyítás is van a dologra (egy generátorfüggvényes és két elemi - utóbbinak külön szépsége, hogy az  szorzót is megmagyarázza), zárójelezés helyett jobbra és felfelé lépkedő, főátló alá nem lépő királlyal. szorzót is megmagyarázza), zárójelezés helyett jobbra és felfelé lépkedő, főátló alá nem lépő királlyal.
|
| Előzmény: [2703] lorantfy, 2008-06-27 11:05:36 |
|
|
|
| [2701] jenei.attila | 2008-06-25 14:53:42 |
 A pn,z-re (ha n z) nem tudok zárt képletet, de pn,n másképp is felírható, ami alapján egy teljes indukciós bizonyítás sikerre kell hogy vezessen. Az összes zárójelezések száma z) nem tudok zárt képletet, de pn,n másképp is felírható, ami alapján egy teljes indukciós bizonyítás sikerre kell hogy vezessen. Az összes zárójelezések száma 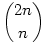 , amiből ki fogjuk vonni a rossz zárójelezések számát. Vezessünk be egy s számlálót 0 kezdőértékkel, amely a zárójelekből álló sztringet elejétől olvasva 1-gyel nő, ha nyitó, illetve 1-gyel csökken, ha záró zárójelet olvasunk. A zárójelezés nyilván akkor romlik el, amikor az s -1 -et vesz fel, ez pedig csak páratlan pozícióban lehet. Pl. nyilván rossz a zárójelezés, ha )-lel kezdődik. Tehát a következőképpen számolunk: A szóban forgó páratlan pozíció (2i+1) előtt befejezett, jó zárójelezés áll (s=0), aztán záró zárójel következik. Ezen esetek száma az előző 2i pozíción létrejövő jó zárójelezések száma (pi,i), szorozva a 2i+2 -edik pozíciótól kezdődő összes zárójelezések számával ( , amiből ki fogjuk vonni a rossz zárójelezések számát. Vezessünk be egy s számlálót 0 kezdőértékkel, amely a zárójelekből álló sztringet elejétől olvasva 1-gyel nő, ha nyitó, illetve 1-gyel csökken, ha záró zárójelet olvasunk. A zárójelezés nyilván akkor romlik el, amikor az s -1 -et vesz fel, ez pedig csak páratlan pozícióban lehet. Pl. nyilván rossz a zárójelezés, ha )-lel kezdődik. Tehát a következőképpen számolunk: A szóban forgó páratlan pozíció (2i+1) előtt befejezett, jó zárójelezés áll (s=0), aztán záró zárójel következik. Ezen esetek száma az előző 2i pozíción létrejövő jó zárójelezések száma (pi,i), szorozva a 2i+2 -edik pozíciótól kezdődő összes zárójelezések számával (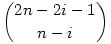 ). Ha i megy 0-tól n-1 -ig, ezek összege megadja az összes rossz zárójelezést. Vagyis: ). Ha i megy 0-tól n-1 -ig, ezek összege megadja az összes rossz zárójelezést. Vagyis:
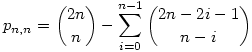
Ebben a rekurzióban már csak egy index szerepel, úgyhogy teljes indukcióval bebizonyítható, hogy a Catalan számokat adja. Sok sikert.
|
| Előzmény: [2700] lorantfy, 2008-06-24 10:55:29 |
|
|
|
|
| [2697] jenei.attila | 2008-06-23 13:03:50 |
 Nem tudom beszúrni a linket. E téma 80. oldal, 685 hsz.
Link javítva - Sirpi
|
|




 [0,1]}
[0,1]}  x
x y
y y akkor átrendezés után
y akkor átrendezés után  -1 (mod 2n-1) kongruencia természetesen előállhat, de ez nem jelenti azt, hogy a bal oldali oszlop teljesen fekete lesz. A zavart az okozza, hogy ha 2m
-1 (mod 2n-1) kongruencia természetesen előállhat, de ez nem jelenti azt, hogy a bal oldali oszlop teljesen fekete lesz. A zavart az okozza, hogy ha 2m q
q
 1 (mod 2n-1), akkor m művelet elvégzése után biztosan újra egyszínű oszlopokat kapunk. Próbálgatással úgy tűnik azonban, hogy kevesebb lépésben ez nem áll elő. Ezt még be kéne bizonyítani. természetesen az m többszörösei is jók, tehát a legkissebb ilyen m-et keressük (1 vagy -1 2-es alapú logaritmusa modulo 2n+1; nem tudom hogy lehet könnyen kiszámítani).
1 (mod 2n-1), akkor m művelet elvégzése után biztosan újra egyszínű oszlopokat kapunk. Próbálgatással úgy tűnik azonban, hogy kevesebb lépésben ez nem áll elő. Ezt még be kéne bizonyítani. természetesen az m többszörösei is jók, tehát a legkissebb ilyen m-et keressük (1 vagy -1 2-es alapú logaritmusa modulo 2n+1; nem tudom hogy lehet könnyen kiszámítani). 
 0 ( ellenkező esetben az abszolút érték miatt vehetjük a -g(x) függvényt ) Ha ábrázoljuk g(x)-et, megállapíthatjuk, hogy 0 és a között nem lehet pontja a -1 meredekségű y = h - ( x - a ) = h + a - x egyenes felett, ugyanis ha valamilyen u-ban g(x) > h + a - u , akkor u és a között lenne olyan v, ahol |g'(v)| > 1. Ugyanígy nem lehet g(x)-nek pontja (0,a) -ban az y = h + x - a egyenes alatt sem. A baloldali integrál abszolut értéke, a görbe alatti terület akkor a legnagyobb, ha a teljes rendelkezésre álló pozitív tartományt kitölti, vagyis
0 ( ellenkező esetben az abszolút érték miatt vehetjük a -g(x) függvényt ) Ha ábrázoljuk g(x)-et, megállapíthatjuk, hogy 0 és a között nem lehet pontja a -1 meredekségű y = h - ( x - a ) = h + a - x egyenes felett, ugyanis ha valamilyen u-ban g(x) > h + a - u , akkor u és a között lenne olyan v, ahol |g'(v)| > 1. Ugyanígy nem lehet g(x)-nek pontja (0,a) -ban az y = h + x - a egyenes alatt sem. A baloldali integrál abszolut értéke, a görbe alatti terület akkor a legnagyobb, ha a teljes rendelkezésre álló pozitív tartományt kitölti, vagyis 

 R deriválható függvény, úgy hogy létezik a
R deriválható függvény, úgy hogy létezik a



