| [3012] m2mm | 2009-08-17 14:50:26 |
 Én találtam egy (lehet hogy elemi[mi számít eleminek?], mindenesetre komplex számok nélküli) megoldást. Legyen a>0, tehát a többi megoldást keressük.
a2+1=b3, tehát a2=b3-1=(b-1)(b2+b+1)=(b-1)((b-1)2+3(b-1)+3). Tetszőleges 3-mal nem egyenlő p prímre, b-1=pkl alakba írható. a2=pk(p2kl3+3pkl2+3l) Ha k>0, akkor p2kl3+3pkl2+3l nem osztható p-vel, tehát k páros. Magyarán b-1=c2, vagy b-1=3c2. Előbbi esetben Q=(b-1)2+3(b-1)+3 négyzetszám, de ((b-1)+1)2<Q<((b-1)+2)2, tehát mégse az: b-1=3c2.Mivel a>0, ezért b>1, tehát c pozitív.
a2+1=(3c2+1)3=27c6+27c4+9c2+1, ebből 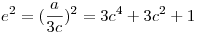 . (c2+1)2<e2<(2c2+1)2. Tehát e c2-tel való osztási maradéka 2,3,4,...,0 lehet(tehát csak 1 nem lehet), mindegyik 1 esetben. e2 c2-tel való osztási maradéka 1. . (c2+1)2<e2<(2c2+1)2. Tehát e c2-tel való osztási maradéka 2,3,4,...,0 lehet(tehát csak 1 nem lehet), mindegyik 1 esetben. e2 c2-tel való osztási maradéka 1.
Tehát e=c2+f, e2=c4+2fc2+f2, e2 f2 f2 12 (modc2), tehát c2|(f-1)(f+1), magyarán f=1 vagy f=c2-1. f=1 nem lehet, tehát e=2c2-1. Tehát 3c4+3c2+1=(2c2-1)2=4c4-4c2+1, 7c2=c4, c>0 miatt 7=c2, tehát c nem egész. Tehát csak az (a,b)=(0,1) számpár megoldás. 12 (modc2), tehát c2|(f-1)(f+1), magyarán f=1 vagy f=c2-1. f=1 nem lehet, tehát e=2c2-1. Tehát 3c4+3c2+1=(2c2-1)2=4c4-4c2+1, 7c2=c4, c>0 miatt 7=c2, tehát c nem egész. Tehát csak az (a,b)=(0,1) számpár megoldás.
|
| Előzmény: [3011] Lóczi Lajos, 2009-08-17 13:54:34 |
|
|
|
| [3009] Higgs | 2009-08-16 16:02:20 |
 Igen, rosszul tettem fel! Az előbb említett eseten kívűl van-e más megoldás is, és ha nincs, akkor hogyan bizonyítható?
|
|
|
| [3007] Higgs | 2009-08-15 21:40:05 |
 Üdv!
Egy négyzetszám+1 lehet egyenlő egy köbszámmal?
|
|
|
| [3005] djuice | 2009-08-12 21:08:56 |
 Sziasztok!
A következő feladatot adnám fejtörés gyanánt: Adottak A és B pontok melyek mozognak egy meghatározott síkban, A-B távolsága mindíg állandó. A pont vízszintesen mozog, B függőlegesen. Ha A-B pontok állandó távolságát pl egy rúddal szemléltetjük, a rúd mozgás során kapott gördülési íve milyen síkgörbével határozható meg? Továbbá ha ezt a rendszert pl egy lezáródó garázsajtóként értelmezzük (merthogy gyakorlati alkalmazásként onnan származik), egy adott H magasságú jármű milyen minimális M távolságra kell beparkoljon a garázsba, hogy a lezáródó ajtó ne ütközzön a tetejének? (nem túl bonyolult feladat, de érdekes paraméteres egyenletet lehet rá felírni) :)
|
|
|
| [3003] MTM | 2009-08-01 13:27:33 |
 Ha van másik 10n+1 alakú prím, akkor annak a négyzete pal., de tudtommal nem ismert másik(és nincs is bizonyítva, hogy nincs több), magyarán ez a kérdés baromi nehéz.
|
| Előzmény: [3000] Radián, 2009-07-22 19:17:50 |
|
|
|
| [3000] Radián | 2009-07-22 19:17:50 |
 Lehet, hogy kicsit elsietem, de nem lehet tudni mikorra lesz meg e probléma megoldása. Kapcsolódó kérdés:
Mely prímeknek van többjegyű palindrom hatványa?(7-nek,11-nek,101-nek van, de vajon rendelkezik e tulajdonsággal még valamelyik másik prím is?)
|
|
| [2999] Radián | 2009-07-22 19:13:37 |
 Csak addig jutottam, hogy 2 hatványai közül csak azok jöhetnek szóba melyek 20-szal való osztási maradéka 1,2,3 v. 16. Gondolom ez a tény semmire se jó de hátha valami csoda folytán valakinek segít:)
|
|
|
| [2997] MTM | 2009-07-19 16:18:36 |
 Üdv!
Van-e 2-nek többjegyű palindromhatványa?
|
|
|
| [2995] sanyi15ka | 2009-06-26 09:43:13 |
 En mashogy oldottam meg, de igy is jo. En inkabb roman modszert hasznaltam, vagyis egy kis rendezessel felirtam 3 egyenlotlenseget es ezek altal bebizonyitottam h csak n=3-ra kompatibilisek az egyenletek es igy megkimeltem magam attol, hogy n=1-t, illetve n=2-t targyaljam.:)
|
| Előzmény: [2994] R.R King, 2009-06-26 08:34:00 |
|
| [2994] R.R King | 2009-06-26 08:34:00 |
 egy pozitív szám és a reciprokának összege legalább 2, így a második egyenletből n legfeljebb 3 lehet.Ha n pl 3 akkor a második egyenlet csak X(i)=1 esetben teljesülhet.Ez teljesíti az első egyenletet is. Ebben az esetben tehát a kérdéses összeg 3. n=1, illetve n=2-tőt rád bízom:)
|
| Előzmény: [2993] sanyi15ka, 2009-06-26 00:32:28 |
|
| [2993] sanyi15ka | 2009-06-26 00:32:28 |
 Udv! 10. vegen megkert minket a matektanarunk, hogy szerkesszunk 2 matek feladatot. Nekem ez lett az egyik. Az e-mail cimemre varom a megoldasokat. Ha lehet akkor a feladatom elemi matekkel legyen megoldva, mert csak jovore, 11-be, tanulok analizist meg felsobb dolgokat es azokat meg nem tudom.
|
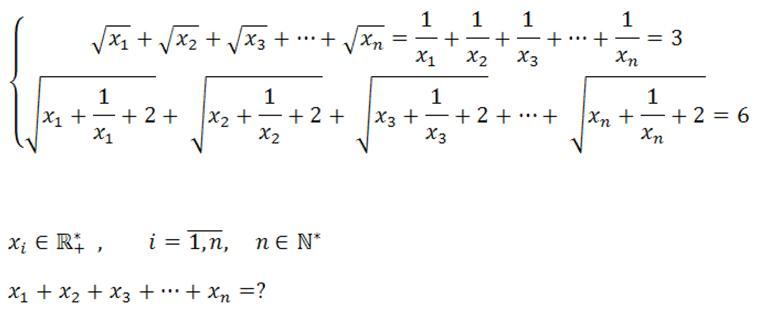 |
|
|
| [2991] m2mm | 2009-06-22 22:08:40 |
 Üdv!
Két idei KöMaL-feladat általánosítása:
Egy májusi feladat:
B. 4185. Mutassuk meg, hogy minden nemnulla polinomnak van olyan nemnulla polinomszorosa, amelyben minden tag kitevője osztható 3-mal.
Ez a (a+b+c)(a2+b2+c2-ab-bc-ca)=a3+b3+c3-3abc azonossággal könnyen kezelhető.
A kérdés: Mely n-ekre igaz az, hogy minden nemnulla polinomnak van olyan nemnulla polinomszorosa, amelyben minden tag kitevője osztható n-nel?
Egy márciusi feladat:
B. 4167. Egy n pozitív egészre jelölje f(n) az n tízes számrendszerbeli alakjának a megfordításával kapható számot. (Tehát f(2500)=52, f(1456)=6541.) Keressük meg azokat a pozitív egész k számokat, amelyekre teljesül, hogy tetszőleges n többszörösükre k az f(n) számnak is osztója.
A kérdés: Mik a keresendő k számok r alapú számrendszerben? (esélyesnek tartom r2-1 osztóit, de nem tudtam bizonyítani)
|
|
|
|
|



 f2
f2