| [3037] nadorp | 2009-10-29 15:24:20 |
 Valamit nem értek vagy nem látok, de szerintem csak azt tudjuk, hogy tetszőleges a-ra
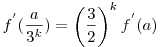 teljesül. Amit Te írtál, ott a jobb oldalon f(a) áll és nem a deriváltja. Hogy jött ez Neked ki ? teljesül. Amit Te írtál, ott a jobb oldalon f(a) áll és nem a deriváltja. Hogy jött ez Neked ki ?
Másrészt az f-ről csak azt tudjuk, hogy deriválható és nem biztos, hogy folytonosan deriválható. Miért teljesül
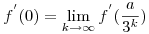
|
| Előzmény: [3035] jenei.attila, 2009-10-29 14:43:51 |
|
| [3036] HoA | 2009-10-29 14:54:54 |
 Én arról az oldalról próbáltam, hogy egészről valósra áttérve igazoljuk, hogy a függvény csak
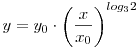
alakú lehet, ahonnan már következik, hogy a 0 -beli deriválhatósággal van a baj.
|
| Előzmény: [3035] jenei.attila, 2009-10-29 14:43:51 |
|
|
| [3034] nadorp | 2009-10-29 14:11:01 |
 Egy hónappal lemaradtam, de találtam egy szinte számolás nélküli megoldást.
yn+1=(1+x)yn+nx2
yn+1+nx=(1+x)(yn+nx)
yn+1+(n+1)x=(1+x)(yn+nx)+x
yn+1+(n+1)x+1=(1+x)(yn+nx+1)
Most már csak fel kell írni a fenti utolsó összefüggést az n=0,1,...,n-1 értékekre és összeszorozni őket. Kapjuk:
yn+nx+1=(1+x)n(y0+0.x+1)=2(1+x)n
yn=2(1+x)n-nx-1
Más:
Lóczi Lajos utolsó példájára szerintem csak az f(x)=0 a megoldás.
|
| Előzmény: [3028] jonas, 2009-09-27 20:46:48 |
|
| [3033] Lóczi Lajos | 2009-10-29 10:47:02 |
 Legyen f olyan valós függvény, amelyik mindenhol értelmezve van és mindenhol deriválható. Tudjuk továbbá, hogy minden valós x esetén f(3x)=2f(x).
Adjuk meg az összes ilyen tulajdonságú f leképezést.
|
|
| [3032] djuice | 2009-10-27 13:25:56 |
 Az angol wiki is foglalkozik vele: http://tinyurl.com/yhhtvkh
|
|
| [3031] djuice | 2009-09-28 19:14:04 |
 NEM SEMMI! Hát le a kalappal, komolyan! Én már nem is merek többet itt kérdezni. :) Egy volt KGB-s se nyomozta volna ki tüzetesebben! :)))
Mindenesetre lelombozó a tény ami a példát illeti, elvesztette minden varázsát.
|
| Előzmény: [3030] Borsos, 2009-09-28 05:55:23 |
|
|
| [3029] jonas | 2009-09-27 20:48:37 |
 „Nem valószínűsíthető hogy hibás lenne, hiszen akkor minek őrizték volna 100 meg 100 éveken át a könyvtárban.”
Kivéve persze, ha csak egy nemrégi átírás vagy fordítás lenne a hibás.
|
| Előzmény: [3027] djuice, 2009-09-27 19:25:51 |
|
| [3028] jonas | 2009-09-27 20:46:48 |
 Én is ilyesmit próbáltam. A különbség az, hogy még kifejtés előtt a rekurziót szétszedtem két részre:
p0=1;pn+1=(1+x)pn
q0=0;qn+1=(1+x)qn+nx2
Ekkor könnyen belátható, hogy
xn=pn+qn
Mármost az első rekurziót triviális feloldani, a másodikat pedig ki kell fejteni, így két olyan összeget kaptam, aminek már ismert a kiszámítási módja, és nekem is végig kéne tudnom számolni, de elrontottam, és nem volt türelmem másodszor is nekiállni.
|
| Előzmény: [3026] Euler, 2009-09-27 13:49:07 |
|
| [3027] djuice | 2009-09-27 19:25:51 |
 Szia Borsos,
Nem valószínűsíthető hogy hibás lenne, hiszen akkor minek őrizték volna 100 meg 100 éveken át a könyvtárban. Erre cáfol az egyetemenünkön egy tanár állítása is, miszerint elképzelhető hogy a feladatot (megírása korában) fejben meg lehetett oldani, nem ám hogy ámítógép meg ezmegaz! :)
Nyilván akkoriban sokkal többen használták a koponyájukat fejszámolásra, mint ma, a kalkulátorok korában. Pl. Bolyai is remekül tudott akkoriban fejben gyököt vonni és 4-5 jegyű számokat összeszorozni, osztani. (mellesleg aki itt közülünk tud ilyet és megosztaná a módszerét, szívesen meghallgatnám, ui állítólag a szorobán oktatás lényege is ez lett volna, hogy vizuálisan tudjon az ember számolni, ne az ujján...)
Szóval a feladatba nekem is beletört minden próbálkozásnál a bicskám, hiába kezdtem az amúgy értelmezni se egyszerű feladatból kifejezni az ismeretleneket... A lényeg hogy lehet több megoldása is, mert a végén a leírás leszűkíti ezeket "négyzet alakba sorakozva", vagyis egész szám aminek gyöke is egész, ill. "3-szögű rend" a csoportosításnál valamilyen egészekből álló sorozatot takar. Ennyire sikerült segítség nélkül rájönnöm. A sorozat elvileg lehet szimmetrikus és asszimmetrikus is, pl így:
|
 |
| Előzmény: [3025] Borsos, 2009-09-26 18:58:55 |
|
| [3026] Euler | 2009-09-27 13:49:07 |
 A helyes válasz: y(n)=2(1+x) az n-ediken-1-nx. A megoldásom menete: feloldottam a rekurziót, ekkor megkaptam y(n)-t, aztán összegeztem egy csomó mértani sorozatot. Ha valakinek van egyszerűbb, kérem irja fel a fórumra.
|
| Előzmény: [3022] Lóczi Lajos, 2009-09-25 23:53:41 |
|
|
|
|
| [3022] Lóczi Lajos | 2009-09-25 23:53:41 |
 Legyen x rögzített valós szám és tekintsük az y0=1,
yn+1=(1+x)yn+nx2
rekurzív sorozatot. Adjuk meg yn explicit alakját csak x és n függvényében.
|
|
|
| [3020] Sirpi | 2009-09-14 09:22:30 |
 234167589133(10) = 110110 10000101 01111001 11011001 00001101(2)
Meg képzelj elé egy csomó 0-t, hogy 64 jegyű legyen. Amíg az első jegy 0, addig a legalsó korong még a helyén van, amíg a 2. nulla, addig az utolsó előtti is, stb. Ebben az állásban a 38. (alulról a 27.) korongot már átmozgattuk (mert az az első 1-es). Ha a köv. helyiértéken 0 lenne, akkor az még rajta lenne a 38. korongon, de mivel 1-es van, ezért már lekerült róla. A köv. jegy 0, ezért a 36. a 37.-en van rajta, aztán 1, vagyis a 35. lekerült róluk stb.
A 4 állapot, amit írtam (00, 01, 10, 11 kezdetek) azt jelzi, hogy az alsó két korong épp milyen állapotban van:
00: mindkettő az eredeti helyén
01: az utolsó előtti átkerül
10: az utolsó átkerül, de az utolsó előtti még nincs rajta
11: mind2 átkerült és egymáson vannak
Ez a gondolatmenet hasonlóan folytatható is az alsó 3, 4 stb korongra, ahogy fent már elemezgettem. Ami ebből nem látszik, hogy melyik korong épp melyik rúdon van, de az valahogy paritásból ki kell, hogy jöjjön, most túl korán van nekem ehhez :-) De ha rá akarsz erre jönni, akkor ne 64 koronggal próbálkozz, hanem mondjuk 3-4-gyel.
|
| Előzmény: [3019] Higgs, 2009-09-13 20:30:32 |
|
| [3019] Higgs | 2009-09-13 20:30:32 |
 Biztos csak nekem nem világos, de a "4 állapotot"-nál elvesztettem a fonalat. Pl. az 234167589133-dik lépés utánni állapotot 64 korongnál hogyan tudhatom meg? Vagy hogyan számolhatom ki a k-adik korong álltal megtett utat a kirakás után, bár ez más kérdés:D
|
| Előzmény: [3018] Sirpi, 2009-09-13 19:40:34 |
|
| [3018] Sirpi | 2009-09-13 19:40:34 |
 Az n 2-es számrendszerbeli alakjából szerintem ki lehet gyorsan következtetni. Pl. az utolsó, k. korong a 2k-1-dik lépésben kerül át a 3. rúdra, és onnan ott marad. hasonlóan a k-1. is 2k-2-dik lépésben kerül át a "rossz" rúdra, majd a 2k-1+2k-2-dik lépésben a jóra. Ezt a 4 állapotot a szám kettes számrendszerbeli eleje jelzi (00, 01, 10, 11). A k-2. korongot már 4-szer fogjuk mozgatni, mindig félidőben a korábbiakhoz képest. Figyelni kell rá, hogy a két szabad közül épp melyikre tesszük le, ezt most nem gondolom végig, valami maradjon Neked is ;-)
|
| Előzmény: [3017] Higgs, 2009-09-13 18:57:46 |
|
| [3017] Higgs | 2009-09-13 18:57:46 |
 Sziasztok!
A következő a kérdésem: Hanoi tornyai feladatnál, hogyan határozhatjuk meg, hogy az n-edik lépés után az egyes korongok melyik rúdon, és milyen magasan fognak elhelyezkedni? (Feltételezve, hogy optimálisan oldjuk meg, vagyis 2 a k-adikon-1 lépésben.)
|
|
| [3016] djuice | 2009-08-25 03:20:34 |
 mégegy igazítás, az ábrán a=4; h<a a helyes jegyzet és a valamint h értékei ismertek (paraméterek)
Ezek után jöjjön a nagy kedvencem:
Hány marhát számlált a Napisten nyája, barátom Gonddal számold ki, hogyha vág az eszed Hányat őriztek Szicília tág legelőin, Négy kisebb részre bontva az isteni nyájt.
Mindegyik rész más színű volt. Hószín a legelső, Egy másik résznek színe sötét fekete. Barna a harmadik, a negyedik meg tarka-iromba. Mindben több a bika és kevesebb a tehén.
Többen voltak a barna bikák ott, mint a fehérek, Mégpedig a feketék harmadával s felivel. Tarkák számának negyedével és ötödével Múlta felül feketék száma a barnákét. Tarkák is túltettek a barnákon a fehérek Egyhatodával s még egyhetedével rá.
így a bikák. Hát a tehenek? Közülük a fehérek A fekete marhák harmadát s negyedét Alkották. Fekete tehenek meg a tarka Marhák egynegyedét, s rá még egyötödét.
Tarka-iromba tehén volt egyötöd- és hatodannyi Ebben a csordában, mint a barna barom. Végül barna tehén hatodannyi s még hetedannyi, Volt mint tiszta fehér marha (tehén s bika is).
Hogyha kiszámítod színenként hány bika volt ott És tehenekből hány - számok mestere vagy. Bölcsnek azonban nem mondhatnak, míg figyelembe Nem veszed azt is, amit még hozzáteszek ím:
Bonts a bikák nyáját két részre: fehér s feketékre Egy részben, másba barna s tarka kerül. Akkor az első rész sorakozhat négyzetalakban S háromszögletű szép rendben a többi bika.
Hogyha a problémát úgy oldod meg, hogy ez is vág Győzelmed teljes, s híres lesz a neved.
(A feladatot 1773-ban egy görög nyelvű kéziratban találta G. E. Lessing a wolfenbütteli könyvtárban.)
Mindent bele! :DD
|
|
| [3015] djuice | 2009-08-24 23:45:26 |
 bocsánat, a kék vonal a grafikonon nem a kapu pályaíve, hanem az ajtó záródásának függvényeként "t" értéke -> t(x)
|
|
| [3014] djuice | 2009-08-24 23:40:37 |
 :)))) Véletlenek nincsenek, sőt! Mivel annyit nem tanítottak meg analízisből hogy egy ilyen, a valós életből származó problémát le tudjon kezelni egy diák így kicsit nekem még középiskolás (paraméteres egyenlet) maradt megoldásnak. Volna miért szégyelnem magam, hogy 1 hónapig rágódtam rajta mire kiizzadtam, de valahogy a hasonló 3szögek ismérvei eszembe sem jutottak, ami végülis a megoldáshoz vezetett. A megrázó az, hogy kínomban már megmutattam itt a Miskolci Egyetemen a matektanáromnak (matematikai tudományok kandidátusa meg minden) és nem tudott vele mit kezdeni!!!!! Sajnos be kellett látnom, hogy aki 40 évig séma szerűen ugyanazt tanítja, "beleszürkül" a dolgokba és ilyen egyszerűbb gyakorlati dolgokat nem tud kezelni.
Szóval a megoldásom:
|
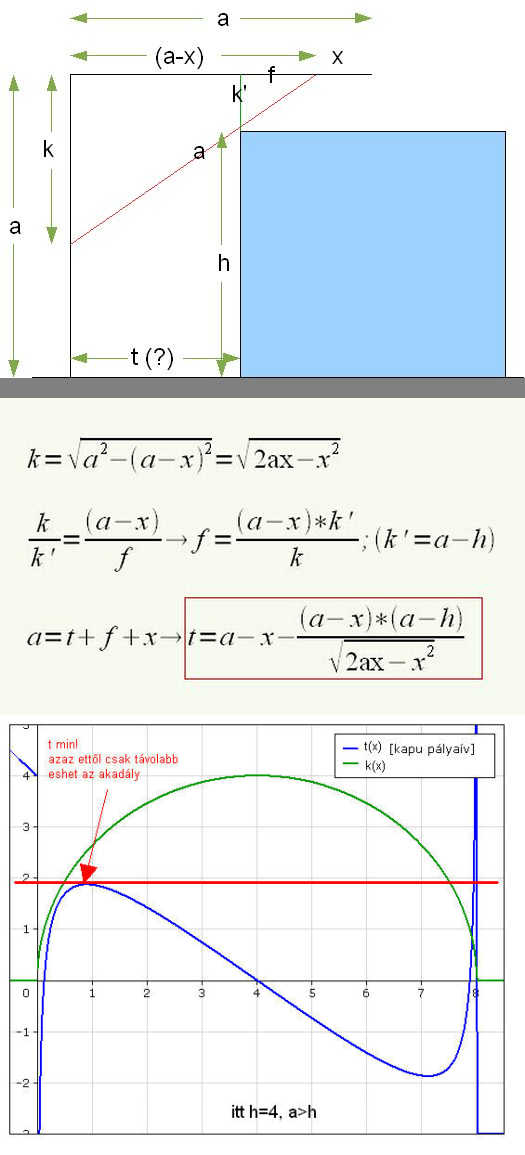 |
| Előzmény: [3006] leni536, 2009-08-12 21:43:45 |
|
|




 0, vagyis f csak akkor deriválható 0-ban, ha f(a)=0 minden a valós számra.
0, vagyis f csak akkor deriválható 0-ban, ha f(a)=0 minden a valós számra.




