|
| [3075] bily71 | 2009-11-29 18:21:36 |
 Adott az ABCD négyzet. Osszuk fel az AB és a BC oldalakat n egyenlő részre. Kössük össze az A csúcsot a BC oldal B-hez közelebbi első osztópontjával, azután az AB oldal A-hoz közelebbi első osztópontját a BC oldal B-hez közelebbi második osztópontjával, sít., végül az AB oldal B-hez közelebbi első osztópontját fogjuk összekötni a C csúccsal. A kapott szakaszok egy görbét érintenek, ami az E pontban metszi a BD átlót. Milyen arányban osztja az E pont az átlót, ha n-et minden határon túl növeljük?
|
|
| [3074] Janosov Milán | 2009-11-29 17:27:54 |
 Hahó!
Egy szerintem érdekes (de nem annyira nehéz feladat):
Írjuk fel a 24-et az 1, 3, 4 és 6 számok és az alapműveletek segítségével úgy, hogy mindegyik számot pontosan egyszer kell felhasználni, zárójelet használhatunk, de a számokat közvetlenül egymás mellé írva többjegyű számokat alkotni nem szabad.
(A feladat egy BME-s felvételivel kapcsolatos újságjából való)
|
|
|
|
|
| [3070] bily71 | 2009-11-29 10:07:49 |
 Nem fokozom, csak leírom a választ.
am+bm=cm, mivel c>a, létezik n egész, hogy c=a+n. Fermat tételéből következik, mivel m prím, hogy
cm c c (a+n)m (a+n)m a+n(mod m) a+n(mod m)
, továbbá
am a(mod m) a(mod m)
bm b(mod m) b(mod m)
, ebből
am+bm a+b a+b a+n(mod m) a+n(mod m)
b n(mod m) n(mod m)
, tehát
b=n+xm
, ahol x nemnegatív egész.
|
| Előzmény: [3067] bily71, 2009-11-28 16:05:53 |
|
|
|
|
|
| [3063] bily71 | 2009-11-27 22:41:08 |
 Igaz-e, hogy ha teljesül az am+bm=cm egyenlőség, akkor teljesül az am+(n+mx)m=(a+n)m egyenlőség is, ahol b=n+mx, c=a+n?
(a<b<c és a,b,c,n,m,x nemnegatív egészek.)
|
|
|
|
| [3060] m2mm | 2009-11-27 22:07:06 |
 Miért lenne 2x2=y2-1 egyenlet összes megoldása x= 2, y= 2, y= 3? 3?
2x2+1=y2-re megoldás az x0=0, x1=2, xn=6xn-1-xn-2 sorozat, ami szig.mon. nő, ergo végtelen sok megoldás van[a következő néhány (x,y) pár a sorozatban (12,17), (70,99), (408,577)].
|
| Előzmény: [3056] bily71, 2009-11-27 21:20:12 |
|
| [3059] bily71 | 2009-11-27 21:50:28 |
 Bocs, elnéztem, a jobb oldal összeg, nem különbség. Hirtelen azt hittem, hogy a második egyenlet egy zárt görbe egyenlete, ami csak véges sok rácsponton haladhat át, de ez egy nyílt görbe egyenlete.
De mivel van ellenpélda, így a válasz: nem igaz.
|
| Előzmény: [3056] bily71, 2009-11-27 21:20:12 |
|
| [3058] RRichi | 2009-11-27 21:45:31 |
 Feladat: Ismert n db prímszám, melyeket összeszorozzuk, az eredményhez hozzáadunk egyet, és az így kapott a számnak vesszük a legkisebb 1-től különböző osztóját, ami biztosan prímszám lesz. Ezt hozzávesszük az ismert prímekhez, és újrakezdjük az algoritmust. Kérdés, hogy bármely kiindulóprímek esetén megkapható e az összes létező prímszám ezzel a módszerrel?
|
|
|
| [3056] bily71 | 2009-11-27 21:20:12 |
 Legyen k=2, tehát nem négyzetszám és l=1, ekkor
2x=y2-1.
Az egyik lehetséges megoldás: x=4, y=3, azaz
2.4=32-1.
A kx2+l=y2, azaz behelyettesítve, átrendezve, az
2x2=y2-1
egyenlet összes megoldása: x= 2, y= 2, y= 3, tehát nem igaz. 3, tehát nem igaz.
A második egyenlet átrendezve:
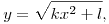
az
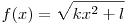
függvénynek véges sok zérushelye van, (0, 1 vagy 2 db.), tehát semmilyen k,l értékek esetén sem lehet végtelen sok megoldás.
|
| Előzmény: [3054] m2mm, 2009-11-27 18:44:02 |
|
|
|
| [3053] BohnerGéza | 2009-11-27 18:32:11 |
 Nem.
x+8=yy (k=1, l=8) egyenletnek van megoldása: (1,3).
Az xx+8=yy egyenletnek csak 4 mo-sa van: (1,3), (1,-3), (-1,3), (-1,-3)
|
| Előzmény: [3052] m2mm, 2009-11-27 14:42:14 |
|
| [3052] m2mm | 2009-11-27 14:42:14 |
 Igaz-e, hogy ha az egész számpárok halmazán van megoldása a kx+l=y2 egyenletnek(k,l adott), akkor végtelen sok megoldása van a kx2+l=y2 egyenletnek?
|
|
|
| [3050] jenei.attila | 2009-10-30 23:45:00 |
 Valóban ugyanaz a konstrukció. Tényleg nem adtam meg az összes fv.-t, és ahogy javasoltad úgy jó fv.-ek konstruálhatók. Elég megadni pl. az [1,3] intervallumon akármilyen deriválható fv.-t, amelyre f(3)=2f(1), és 3-ban a balodali derivált értéke az 1-beli jobboldali derivált értékének 2/3-szorosa. A többi a már általad leírt módon mehet tovább. Ilyen módon valóban az összes megfelelő fv.-t megadjuk (a 0-beli deriválhatóság természetesen nem teljesíthető).
|
| Előzmény: [3049] HoA, 2009-10-30 13:24:23 |
|







 c
c 2, y=
2, y=

