|
| [3115] Róbert Gida | 2009-12-19 14:28:38 |
 Csak annyi a lényeges, hogy C(x)=n, (nem érdekes, hogy fixpontnál x=n). Mert akkor n csak nagyon kevés féle szám lehet, konkrétan binomial(d+9,9), ha n legfeljebb d jegyű. Ez d=21-re is csak 14307150 (ha x az hosszabb, mint 21 jegy,akkor C(x)<x, így nem lehet fixpont), ez pedig egy perc alatt végignézhető. Egy gráf is építhető, élnek egy (x,C(x)) felel meg. Hosszabb ciklusok keresése is ugyanígy mehet, tulajdonképpen az összes kört is megkereshetnénk, diszjunkt irányított körök (esetleg kettő hosszúak) és hurokélek uniójára esik szét a gráf, hiszen minden kifok 1 a gráfban. (minden 21-nél hosszabb szám elég sok iteráció után 21-nél rövidebbre esik, így itt is elég ezeket nézni).
|
| Előzmény: [3114] Lóczi Lajos, 2009-12-19 12:22:37 |
|
| [3114] Lóczi Lajos | 2009-12-19 12:22:37 |
 Kíváncsi lennék, hogy a fixpontokat milyen egyszerűsítési feltevésekkel/esetszétválasztásokkal/algoritmussal állítottad elő konkrétan.
Találtál esetleg menet közben 2-nél hosszabb ciklust? (Én eddig csak ilyenre bukkantam rá.)
|
| Előzmény: [3112] Róbert Gida, 2009-12-19 00:26:20 |
|
|
| [3112] Róbert Gida | 2009-12-19 00:26:20 |
 10-es számrendszerben összesen 109 fixpont van, éspedig:
22,10213223,10311233,10313314,10313315,10313316,10313317,10313318,10313319,21322314, 21322315,21322316,21322317,21322318,21322319,31123314,31123315,31123316,31123317,31123318, 31123319,31331415,31331416,31331417,31331418,31331419,31331516,31331517,31331518,31331519, 31331617,31331618,31331619,31331718,31331719,31331819,1031223314,1031223315,1031223316, 1031223317,1031223318,1031223319,3122331415,3122331416,3122331417,3122331418,3122331419, 3122331516,3122331517,3122331518,3122331519,3122331617,3122331618,3122331619,3122331718, 3122331719,3122331819,10413223241516,10413223241517,10413223241518,10413223241519, 10413223241617,10413223241618,10413223241619,10413223241718,10413223241719,10413223241819, 41322324151617,41322324151618,41322324151619,41322324151718,41322324151719,41322324151819, 41322324161718,41322324161719,41322324161819,41322324171819,1051322314251617, 1051322314251618,1051322314251619,1051322314251718,1051322314251719,1051322314251819, 1051322325161718,1051322325161719,1051322325161819,1051322325171819,5132231425161718, 5132231425161719,5132231425161819,5132231425171819,5132232516171819,106132231415261718, 106132231415261719,106132231415261819,106132231426171819,106132231526171819, 613223141526171819,1011112131415161718,1011112131415161719,1011112131415161819, 1011112131415171819,1011112131416171819,1011112131516171819,1011112141516171819, 1011113141516171819,1111213141516171819,10713223141516271819,101112213141516171819
|
| Előzmény: [3110] Sirpi, 2009-12-17 12:00:10 |
|
| [3111] Lóczi Lajos | 2009-12-18 00:22:57 |
 Ezzel kapcsolatban érdekes volt megfigyelni azt, hogy a legkisebb fixpontok minden számrendszerben csupa egyforma számjegyből állnak. (Vajon ezt a tényt külön be lehetne/lehetett volna látni a konkrét értékek ismerete nélkül?)
|
| Előzmény: [3110] Sirpi, 2009-12-17 12:00:10 |
|
| [3110] Sirpi | 2009-12-17 12:00:10 |
 Kicsit átírtam a progit, hogy más számrendszerekkel is menjen. Ezeket találtam a kül. számrendszerekre:
2-es: 111, 1101001
3-as: 22, 10111, 11112, 100101, 2021102, 1011122, 10010122
4-es: 22, 1011112, 1011113, 1111213, 10213223, 10311233, 101112213
5-ös: 22, 10213223, 10311233, 10313314, 21322314, 31123314, 101111x1y (1<x<y), 10111221314
Elvileg ezekre nincs is más megoldás.
10-esre ezek a legfeljebb 8-jegyű megoldások, itt is csak pár sorozat van (3<x<y): 22, 10213223, 10311233, 1031331x, 2132231x, 3112331x, 31331x1y
És ugye igaz, hogy ha van olyan megoldás, ahol minden darabszám egyjegyű, akkor az minden magasabb számrendszerben is megoldás lesz.
|
|
| [3109] Sirpi | 2009-12-14 13:09:39 |
 Nem írtam át a progit a 2-es számrendszer kezelésére (amúgy is csak otthon van meg, ezt meg a villamoson agyaltam reggel fejben). De akkor kicsit kipofozom majd.
|
| Előzmény: [3108] jonas, 2009-12-14 11:33:27 |
|
| [3108] jonas | 2009-12-14 11:33:27 |
 Érdekes, azt gondoltam, hogy a kettes számrendszerbeli kis megoldásokat számítógéppel könnyen megtalálod. Van pontosan egy kisebb is a 1101001-nél.
|
| Előzmény: [3107] Sirpi, 2009-12-14 09:17:31 |
|
| [3107] Sirpi | 2009-12-14 09:17:31 |
 Ez a C függvény más számrendszerek esetén is érdekes lehet. Pl. 2-es számrendszernél szenvedtem egy kicsit, mire összehoztam a 1101001 számot (tudtok még?). Itt ugyanis nem megy a 22, mint legkisebb megoldás, ami minden más számrendszernél működik.
|
| Előzmény: [3096] Lóczi Lajos, 2009-12-12 11:16:37 |
|
|
|
| [3104] jonas | 2009-12-13 14:36:06 |
 A C függvényről szóló 6. feladat nem nehéz. Könnyű látni, hogy ha n legfeljebb 10n jegyből áll, akkor C(n) legfeljebb 10(n+1) jegyből. Így aztán 30 jegyűnél hosszabb fixpont nem létezhet, tehát kell lennie legnagyobb fixpontnak. Ugyanez részben megoldja az 5. feladatot is, ugyanis azt bizonyítja, hogy minden számból indulva előbb-utóbb olyan ciklusba esünk, amiben minden elem legfeljebb 101030, így a ciklus is legfeljebb ilyen hosszú. Hasonlóan viszont azt is könnyű látni, hogy van tetszőlegesen hosszú átmeneti szakasz, mert ha n legalább 10.10n jegyű, akkor C(n) legalább 1+n jegyű (vagy valami hasonló egyenlőtlenség igaz).
A 3. és 4. feladatot feltehetően kimerítő kereséssel meg lehet válaszolni, kivéve ha valamiért nincsen 2-es ciklus, vagy a legkisebb is nagyon nagy.
|
| Előzmény: [3103] Lóczi Lajos, 2009-12-13 01:15:16 |
|
| [3103] Lóczi Lajos | 2009-12-13 01:15:16 |
 Következzen végül néhány újabb kérdés és sejtés a C függvény kapcsán, amelyek természetes módon felmerülnek és amelyek között szerintem nehezebbek is vannak. (A saját tippjeimet egyelőre nem írom ide, hogy ne befolyásoljak senkit.)
Egy n szám 2-es ciklus, ha C(n) n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is. n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is.
3. feladat. Melyik az a legkisebb n, amely (a C leképezés iterációja során) előbb-utóbb 2-es ciklust eredményez?
4. feladat. Melyik az a legkisebb n, amely rögtön egy 2-es ciklus egyik tagja?
5. feladat. Igaz-e, hogy minden kezdőértékre a C iteráltjaiból alkotott sorozat előbb-utóbb ciklikussá válik? Ha igen, van-e tetszőlegesen hosszú "átmeneti szakasz", mielőtt a sorozat ciklizálni kezd? Van-e maximális ciklushossz, vagy pedig tetszőlegesen hosszú ciklusok előfordulhatnak?
6. feladat. Igaz-e, hogy C-nek van legnagyobb fixpontja? Ha igen, konkrétan melyik szám az?
A fenti C leképezést egyébként a Conway-féle "look and say" sorozat mintájára gyártottam, csak annál egyszerűbb. A Conway-féle sorozat sok érdekes tulajdonsággal bír, különösen meghökkentő a rá vonatkozó "cosmological theorem".
|
| Előzmény: [3096] Lóczi Lajos, 2009-12-12 11:16:37 |
|
| [3102] Radián | 2009-12-12 19:41:48 |
 Ha vesszük a hatjegyűeket, ott 3 db különböző számjegy kell szerepeljen. A szám mindegy jegye kisebb az 5-nél. Ha a számok C(n) alakját akarom felírni az alábbi esetek állhatnak fenn:
1.) 4db x 1db y 1db z (a 4-es és 2 db 1-es sorrendje persze más is lehet, 1,4,1 1,1,4.) Tehát a számban biztosan fog szerepelni az 1,4,q számjegyek. 1-esből biztosan kell legyen legalább 2 db a C(n) felírás alapján, így a számban csak 4 db 1-es fordulhat elő, de ekkor nem az 1. ponti lenne a C(n) alak.
2.) 2db x 2db y 2db z Az 1. ponthoz hasonlóan n kellene tartalmazzon 3 db 2-est ,azaz C(n) alakjába kellene legyen egy 3db q alakú rész. Tehát ez az eset sem állhat elő.
3.) 1db x 2db y 3db z (Az 1,2,3 sorrendje más is lehet.) A szám eredeti alakjába tehát kell szerepeljen 1-es 2-es és 3-as, ezzel meg van az összes különböző jegy. Mivel x,y,z nem egyenlő egymással, így 1-esből 2-esből és 3-masból is több mint egy jegy fog szerepelni a számban, tehát nem lehet a C(n) alakja a 3. pontbeli.
|
| Előzmény: [3101] Radián, 2009-12-12 19:17:27 |
|
| [3101] Radián | 2009-12-12 19:17:27 |
 A négyjegyűeket átfutottam. Egyik se lett jó. Elvileg csak a hatjegyűek között akadhat kisebb, de ezeket nem néztem meg rendesen. 4 jegyűeknél a szám pontosan két különböző számjegyet kell tartalmazzon, ráadásul mindkét jegyből 2-2 db van. E jegyek pedig a 0,1,2 közül kerülhetnek ki. Mivel mindkét jegyből 2-2 db van, ezért a keresett számok csak 2x2x alakúak lehetnek melyek nyilván nem egyenlők a hozzájuk rendelhető C(2x2x)-szel.
|
| Előzmény: [3099] Valezius, 2009-12-12 18:07:21 |
|
| [3100] Sirpi | 2009-12-12 18:17:40 |
 5 perc alatt összeütöttem rá egy progit, amiből kiderült, hogy ez-e a 2. legkisebb... Annyit mindenesetre elárulok, hogy legfeljebb 8 jegyű megoldás 36 db van.
|
| Előzmény: [3099] Valezius, 2009-12-12 18:07:21 |
|
| [3099] Valezius | 2009-12-12 18:07:21 |
 Ha 8 jegyűt keresünk, akkor 10-val kell kezdődnie, a 3. jegy 0,1,2 lehet, amiből a 0 nem lehet, de az 1 sem, hisz ez a helyiérték az egyesek számát mutatja. 1021x2yz alakú számok maradtak. x legalább 3. És ekkor kijön, amit írtál. Amiről elhiszem, hogy kisebb, mint az enyém :) Tehát ha van kisebb, akkor az 4 vagy 6 jegyű lehet.
|
| Előzmény: [3098] Radián, 2009-12-12 16:12:24 |
|
|
|
| [3096] Lóczi Lajos | 2009-12-12 11:16:37 |
 Vezessük be a következő, C-vel jelölt függvényt.
C egy tízes számrendszerbeli pozitív egészhez egy ugyanilyen típusú számot rendel. A számok nem kezdődhetnek 0-val.
Ha n egy pozitív egész, akkor C(n) értéke legyen az a szám, amelyet úgy kapunk, hogy számjegyenként nagyság szerint sorban megszámoljuk, hogy az illető jegyből az n szám összesen hány darabot tartalmaz, ezt leírjuk, majd rögtön utána hozzáírjuk a számjegyet magát, és ezt minden szereplő jegyre megismételjük folytatólagosan leírva.
Például C(2009)=201219, mert 2009-ben (számjegyek szerint növekvő sorrendben) található "2 darab 0", "1 darab 2-es" és "1 darab 9-es".
Egy másik példa: C(31415927)=21121314151719.
Ha valamely számjegy nem szerepel n-ben, azt C nem veszi figyelembe, tehát nem mondunk olyat, hogy pl. "nulla darab egyes".
Egy n szám a C függvénynek fixpontja, ha C(n)=n.
1. feladat: Keressük meg C legkisebb fixpontját.
2. feladat: Keressük meg C második legkisebb fixpontját.
|
|
| [3095] bily71 | 2009-12-02 11:59:04 |
 Valószínűleg megbuktatnának :) Nem okoskodok tovább, igazatok van, inkább sokak örömére visszavonulok, nagyon keveset tudok, én itt esetleg csak kérdezhetek, ide nem elég a matek szeretete, itt tényleg zsenik vannak, valóban ez nem az a fórum... Inkább ezt a pár hónapot a felvételire való felkészüléssel kellene töltenem, elvégre sok bepótolni valóm van.
|
| Előzmény: [3094] nadorp, 2009-12-02 08:52:48 |
|
| [3094] nadorp | 2009-12-02 08:52:48 |
 Nem tudom mit szólnának hozzá egy számelmélet vizsgán
"...ergó n|mx, mivel m prím, ezért n|x"
1) ha 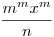 egész, akkor csak az következik, hogy n|mmxm. Az állításod első fele csak akkor igaz ha n prím ( 12|33.143, de 12 egész, akkor csak az következik, hogy n|mmxm. Az állításod első fele csak akkor igaz ha n prím ( 12|33.143, de 12|3.14)
2) 18|3.30, mivel 3 prím ezért 18|30 ?????????????
|
| Előzmény: [3092] bily71, 2009-12-01 12:02:44 |
|
| [3093] bily71 | 2009-12-01 14:21:22 |
 Persze abból, hogy n|x, még nem következik, hogy m|a, csak érdekesnek találtam, így leírtam. Egyébként, ha m=2, akkor igaz minden esetben, hogy 2|a, mivel a és b közül az egyik páros, és igazából nincs jelentősége annak, hogy a két négyzetszám közül, amelyek összege is négyzetszám, melyiket jelöljük a-val, jelölhetjük mindig a párosat.
|
| Előzmény: [3092] bily71, 2009-12-01 12:02:44 |
|
| [3092] bily71 | 2009-12-01 12:02:44 |
 Folytatva:
am+(n+mx)m=(n+a)m
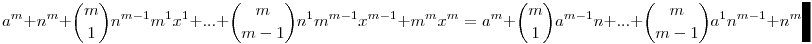
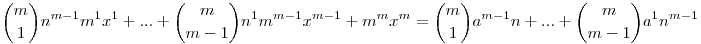
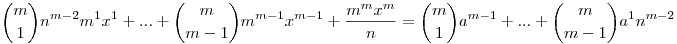
A jobb oldali tört elötti, és a bal oldali összeg értéke egész, ebből következik, hogy a tört értéke is egész, ergó n|mx, mivel m prím, ezért n|x. Tehát
am+(n(my+1))m=(n+a)m
|
| Előzmény: [3087] bily71, 2009-11-30 23:38:47 |
|






 n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is.
n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is. 
