|
| [3228] lgdt | 2010-02-10 19:46:38 |
 Látom, már megoldódott. Lehet, hogy senkit nem érdekel, de azért leírom, hogy hogyan jutottam megoldáshoz az undorítóan bonyolult gondolatmenetemmel:
Mivel f( ) folytonos, ha ) folytonos, ha  >1-re lehetne negatív, akkor 0 is lenne valahol, azaz a determináns harmadik sorát ki lehetne hozni az első kettő >1-re lehetne negatív, akkor 0 is lenne valahol, azaz a determináns harmadik sorát ki lehetne hozni az első kettő  1-gyel és 1-gyel és  2-vel súlyozott lineáris kombinációjaként. Ez pedig azt jelentené, hogy a 2-vel súlyozott lineáris kombinációjaként. Ez pedig azt jelentené, hogy a 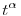 függvényt három helyen is metszené a függvényt három helyen is metszené a  1+ 1+ 2t egyenes, ami - ahogy neked is ezen múlott - a függvény konkáv volta miatt nem lehetséges. 2t egyenes, ami - ahogy neked is ezen múlott - a függvény konkáv volta miatt nem lehetséges.
|
| Előzmény: [3225] Ali, 2010-02-09 11:14:23 |
|
|
| [3227] Fálesz Mihály | 2010-02-10 10:34:19 |
 A derivált használatát el lehet kerülni.
Ha az x,y,z számok különbözők, akkor
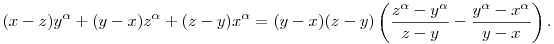
Ha   1 vagy 1 vagy   0, akkor a 0, akkor a  függvény konvex, tehát az utolsó tényező nemnegatív. függvény konvex, tehát az utolsó tényező nemnegatív.
Ha 0   1, akkor 1, akkor  konkáv, és az utolsó tényező nempozitív. konkáv, és az utolsó tényező nempozitív.
(Ez lényegében ugyanaz, mint Ali megoldása.)
Egy kapcsolódó KöMaL feladat itt olvasható.
|
| Előzmény: [3225] Ali, 2010-02-09 11:14:23 |
|
| [3225] Ali | 2010-02-09 11:14:23 |
 Ha  > 1, akkor f > 1, akkor f  0, ha 0 < 0, ha 0 <  < 1, akkor f < 1, akkor f  0. Ha pedig 0. Ha pedig  =0 vagy =1, akkor f=0. Ha x=0, akkor triviális. =0 vagy =1, akkor f=0. Ha x=0, akkor triviális.
Legyen y=ux, z=vy=uvx. Feltehető tehát, hogy x > 0, u,v > 1
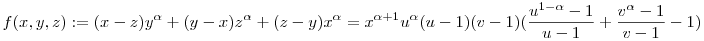
Ismert, hogy konvex és differenciálható g fv-re 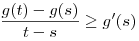 , ahol t > s. Ha g konkáv, akkor az ellenkező irányú egyenlőtlenség áll fenn. Legyen g(x):=xa. , ahol t > s. Ha g konkáv, akkor az ellenkező irányú egyenlőtlenség áll fenn. Legyen g(x):=xa.
g konvex, ha a>1, illetve a<0, konkáv, ha 0<a<1. Ezért ha  > 1, akkor > 1, akkor 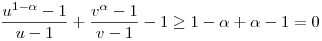 . Ha pedig 0 < . Ha pedig 0 <  < 1, akkor < 1, akkor 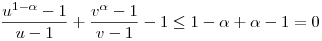 . .
f-re is ugyanez igaz, mivel 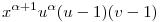 > 0. > 0.
|
| Előzmény: [3201] sakkmath, 2010-02-05 15:18:09 |
|
|
| [3223] Róbert Gida | 2010-02-08 22:02:04 |
 n=2,p=5-re nem igaz a kongruenciád. Ahhoz, hogy jó legyen  (p)-1 kell a kitevőbe, továbbá p lehet páros is. És persze ezt nem p prím esetén Euler-Fermat tételnek hívják, és nem kis-Fermat tételnek. (p)-1 kell a kitevőbe, továbbá p lehet páros is. És persze ezt nem p prím esetén Euler-Fermat tételnek hívják, és nem kis-Fermat tételnek.
|
| Előzmény: [3221] Sirpi, 2010-02-08 10:52:51 |
|
| [3222] Fernando | 2010-02-08 11:27:47 |
 Kedves Bily71!
A Fermat-álprímekről (341 Fermat-álprím 2-es alapra nézve), Carmichael számokról (pl. 561) és a Fermat-tétel megfordításának lehetőségiről olvashatsz: "Megyesi László: Bevezetés a számelméletbe" című könyvében (Polygon, Szeged 1997)
|
| Előzmény: [3212] bily71, 2010-02-07 19:23:42 |
|
|
|
| [3219] Sirpi | 2010-02-08 09:15:16 |
 RG sajátságos stílusával azt próbálta sugallni, hogy ez az összefüggés prímekre pl. ekvivalens a kis-Fermat tétellel (sőt, a következő átalakításnál csak azt használom ki, hogy p páratlan poz. egész):
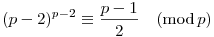
2.(p-2)p-2 p-1 p-1
-2.(p-2)p-2 -(p-1) -(p-1)
(p-2).(p-2)p-2 1 1
(p-2)p-1 1 1
Ez meg tényleg a kis-Fermat a=p-2-es alapra. Már ez az alap is nagyon sok nem-prímet lebuktat, de ha további alapokat is nézünk, akkor egyre biztosabban eldönthető, hogy p prím-e. Egyébként ez a prímteszt erősíthető (Rabin-Miller-féle prímteszt):
Legyen p-1=2m.k, és vegyünk egy 1<a<p-1 alapot. Számítsuk ki az ak,a2k,a4k,...,a2mk=ap-1 számokat (az elsőt "bináris" hatványozással, a többit mindig az előzőből sima négyzetre emeléssel).
Ha az utolsó nem 1 maradékot ad p-vel osztva, akkor p biztosan összetett. Ha már ak 1, akkor a teszt nem tud semmit mondani. Ellenkező esetben viszont van néhány 1-től különböző elem a sorozatban, aztán a végén néhány 1-es. Van tehát egy utolsó, 1-től különböző elem. Ha ez nem -1, akkor p összetett, ez a teszt lényege (ha p prím, akkor az x2 1, akkor a teszt nem tud semmit mondani. Ellenkező esetben viszont van néhány 1-től különböző elem a sorozatban, aztán a végén néhány 1-es. Van tehát egy utolsó, 1-től különböző elem. Ha ez nem -1, akkor p összetett, ez a teszt lényege (ha p prím, akkor az x2 1-nek csak 2 megoldása lehet, az 1 és a -1). 1-nek csak 2 megoldása lehet, az 1 és a -1).
Bizonyítható, hogy adott p összetett számra a szóba jöhető a-k legfeljebb negyede nem buktatja le p összetettségét, vagyis pl. 20 véletlen a-t választva 1/420 esélye lesz annak, hogy p összetett és ez mégse derült ki. A teszt viszont hiába buktatja le p-t, semmilyen támpontot nem ad p osztóira.
|
| Előzmény: [3218] Róbert Gida, 2010-02-07 22:48:06 |
|
|
|
|
|
|
|
| [3212] bily71 | 2010-02-07 19:23:42 |
 Igaz-e, hogy, ha p P, azaz prím, akkor P, azaz prím, akkor
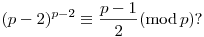
|
|
|
| [3210] lgdt | 2010-02-06 14:23:19 |
 Hát izé. A vektort megszorozhatjuk annyival, hogy a nem 0 koordinátái mind 1-nél nagyobbak legyenek, és ettől a determináns előjele nem változik. Ekkor viszont f( ) monoton növő és folytonos. ) monoton növő és folytonos.
|
| Előzmény: [3209] sakkmath, 2010-02-06 13:43:09 |
|
|
| [3208] lgdt | 2010-02-06 12:34:11 |
 Hasonlóan 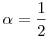 jó a b) feladatra, csak ki kell cserélni az utolsó két sort, ezért lesz a determináns negatív. És intuitíve ha jó a b) feladatra, csak ki kell cserélni az utolsó két sort, ezért lesz a determináns negatív. És intuitíve ha  >1, akkor a koordinátánkénti hatványozás "ugyanúgy" forgatja el az (x,y,z) vektort, mint az >1, akkor a koordinátánkénti hatványozás "ugyanúgy" forgatja el az (x,y,z) vektort, mint az  =2 esetben, ezért az előjeles térfogat pozitív marad. Szóval azt sejtem, hogy =2 esetben, ezért az előjeles térfogat pozitív marad. Szóval azt sejtem, hogy  <1-re f <1-re f 0, 0,  =1-re f=0 és =1-re f=0 és  >1-re f >1-re f 0. 0.
|
| Előzmény: [3207] lgdt, 2010-02-06 01:23:54 |
|
|
|
|



 ) folytonos, ha
) folytonos, ha  1-gyel és
1-gyel és 
 1 vagy
1 vagy  0, akkor a
0, akkor a 


 (p)-1 kell a kitevőbe, továbbá p lehet páros is. És persze ezt nem p prím esetén Euler-Fermat tételnek hívják, és nem kis-Fermat tételnek.
(p)-1 kell a kitevőbe, továbbá p lehet páros is. És persze ezt nem p prím esetén Euler-Fermat tételnek hívják, és nem kis-Fermat tételnek.

 P, n
P, n p-1
p-1
