|
| [3253] bily71 | 2010-02-16 20:04:32 |
 Ez a kongruenciarendszer minden természetes számot lefed a 0-án kívül, tehát részleges lefedőrendszer. Változtassunk egy kicsit a szabályokon. Legyen az ![x_n\equiv\left[\frac{p_n}{6}\right]~(\mod{p_n})](keplet.cgi?k=9446EE673F8A0723) kongruenciáknak megfelelő számtani sorozatok első eleme kongruenciáknak megfelelő számtani sorozatok első eleme ![p_n+\left[\frac{p_n}{6}\right]](keplet.cgi?k=6C0902C528816160) , az , az ![x_m\equiv-\left[\frac{p_m}{6}\right]~(\mod{p_m})](keplet.cgi?k=F051519F148EC06D) kongruenciáknak megfelelőeknek pedig változatlanul kongruenciáknak megfelelőeknek pedig változatlanul ![-\left[\frac{p_m}{6}\right]](keplet.cgi?k=728CDC07E3F05BB2) . .
Nevezzük az ilyen rendszereket, ahol a kongruenciáknak megfelelő számok sorozata nem a maradékosztályt reprezentáló legkisebb elemtől indul, számtani sorozatok lefedőrendszerének, ha minden természetes szám tagja legalább egy sorozatnak. Számtani sorozatok részleges lefedőrendszerének pedig akkor, ha létezik k>0 természetes szám, úgy, hogy a rendszer minden k-nál nagyobb számot lefed.
Utolsó kérdésem e témában: 1. Az így kapott számtani sorozatok rendszere részleges lefedőrendszer-e, vagyis a le nem fedett számok halmaza véges, avagy végtelen?
Mégegyszer elnézést kérek a témakör érdektelenségéért.
|
| Előzmény: [3248] bily71, 2010-02-14 23:10:38 |
|
|
| [3251] Fálesz Mihály | 2010-02-15 10:16:11 |
 Én pontosan fordítva szervezném a számolást:
1. eset: a -1 nem kvadradikus maradék mod p, azaz minden pár két különböző maradékból áll. A párok száma (p-1)/2. A Wilson-tételt is alkalmazva,
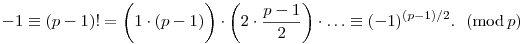 | (1) |
Mivel p>2, a +1 és -1 maradékok különbözőek, a -1 (-1)(p-1)/2 (mod p) kongruencia akkor teljesül, ha (p-1)/2 páratlan, azaz p 4k+3 alakú. (-1)(p-1)/2 (mod p) kongruencia akkor teljesül, ha (p-1)/2 páratlan, azaz p 4k+3 alakú.
2. eset: a -1 kvadradikus maradék mod p, azaz létezik egy a maradék, amire a2 -1(mod p). Ilyen maradék a -a is, a két maradék külöböző, mert p páratlan, és több nincs. -1(mod p). Ilyen maradék a -a is, a két maradék külöböző, mert p páratlan, és több nincs.
Az (1)-beli szorzatból hagyjuk el a (a,a) és a (-a,-a) párokat, és helyettük vegyük hozzá a szorzathoz az (a,-a) párt (ahol a.(-a)=-a2 +1(mod p)): +1(mod p)):
-1 (p-1)!=(a.(-a)).(1.(p-1)).... (p-1)!=(a.(-a)).(1.(p-1)).... (-1)(p-3)/2. (mod p) (-1)(p-3)/2. (mod p) | (2) |
A -1 (-1)(p-3)/2 (mod p) kongruencia akkor teljesül, ha (p-3)/2 páratlan, azaz p 4k+1 alakú. (-1)(p-3)/2 (mod p) kongruencia akkor teljesül, ha (p-3)/2 páratlan, azaz p 4k+1 alakú.
Összességében az derült ki, hogy a -1 akkor és csak akkor kvadradikus maradék mod p, ha p 4k+1 alakú.
|
| Előzmény: [3250] bily71, 2010-02-14 23:27:08 |
|
|
|
| [3248] bily71 | 2010-02-14 23:10:38 |
 Tehát, ha jól értem azt állítod, hogy az
x1 m(mod p1) m(mod p1)
x2 m(mod p2) m(mod p2)
...
xn m(mod pn) m(mod pn)
végtelen kongruenciarendszer lefedőrendszer?
Szerintem nem.
Bármelyik számot fedem le az összes kongruenciával, az ugyanaz, mintha a 0-át fedném le. Az eratoszthenészi szita működik akkor is, ha nem a 0-ról indítjuk a lépéseket, hanem m-ről, hiszen minden modulus prím, csak ebben az esetben nem a pl. 5-tel osztható számokat húzzuk le, hanem m-től minden 5k-adik számot.
Ha pedig arra gondoltál, hogy minden kongruenciával másik számot fedünk le, azt egy esetként írtam le, vagyis a végtelen sok megoldást egy típusba soroltam.
De mi a helyzet akkor, ha minden 3-nál nagyobb prímet kétszer használunk fel, és ha a lefedett szám függ a modulustól, mint a következő rendszerben:
x1 1(mod 5) 1(mod 5)
x2 -1(mod 5) -1(mod 5)
x3 1(mod 7) 1(mod 7)
x4 -1(mod 7) -1(mod 7)
x5 2(mod 11) 2(mod 11)
...
](keplet.cgi?k=31B7602D9EBE3CC4)
,](keplet.cgi?k=65AD1F2195D695B8)
ahol ha pn=6k+1, akkor ![\left[\frac{p_n}{6}\right]](keplet.cgi?k=EC986CB74BE95A64) az alsó egészrészt jelöli, ha pn=6k-1, akkor pedig a felsőt? Lehet-e ez a rendszer részleges lefedőrendszer, tehát létezik-e olyan természetes szám, hogy minden nála nagyobbat lefed a rendszer? az alsó egészrészt jelöli, ha pn=6k-1, akkor pedig a felsőt? Lehet-e ez a rendszer részleges lefedőrendszer, tehát létezik-e olyan természetes szám, hogy minden nála nagyobbat lefed a rendszer?
|
| Előzmény: [3246] jonas, 2010-02-14 17:18:58 |
|
| [3247] bily71 | 2010-02-14 22:12:36 |
 Ezt kapjuk:
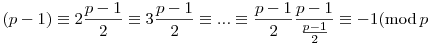
.
Két eset lehetséges, első:
2 |  , ekkor van , ekkor van  darab számpárunk, amelyek szorzata ab darab számpárunk, amelyek szorzata ab -1(mod p), ha behelyettesítünk, akkor ezt kapjuk: -1(mod p), ha behelyettesítünk, akkor ezt kapjuk:

.
Második:
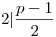 , ekkor létezik a, hogy a2 , ekkor létezik a, hogy a2 -1(mod p), de akkor (p-1)2 -1(mod p), de akkor (p-1)2 -1(mod p). Így kapunk -1(mod p). Így kapunk  darab számpárt, amelyek szorzata ab darab számpárt, amelyek szorzata ab -1(mod p), és mivel 2 -1(mod p), és mivel 2 |  , ezért, ha behelyettesítünk, ezt kapjuk: , ezért, ha behelyettesítünk, ezt kapjuk:

.
|
| Előzmény: [3243] Fálesz Mihály, 2010-02-13 12:38:17 |
|
| [3246] jonas | 2010-02-14 17:18:58 |
 Ne viccelj már. Ha végtelen sok kongruenciát használhatsz, és csak a modulusokra van megkötés, akkor nagyon sok megoldás van, mert akár minden kongruenciával elég egy egész számot lefedned.
|
| Előzmény: [3244] bily71, 2010-02-13 12:46:49 |
|
|
| [3244] bily71 | 2010-02-13 12:46:49 |
 Triviális megoldás az
x1 1(mod p1) 1(mod p1)
x2 2(mod p2) 2(mod p2)
...
xn n(mod pn), n(mod pn),
kongruenciarendszer, ahol n végig fut a természetes számokon, pn>n és a prímek páronkét különböznek.
A p1<p2<...<pn nem szükséges feltétel, pn itt nem az n-edik prímet jelöli és nem szükséges minden prímet felhasználni, akár végtelen sok is kimaradhat.
Egy másik:
x1 a1(mod p1) a1(mod p1)
x2 a2(mod p2) a2(mod p2)
x3 a3(mod p3) a3(mod p3)
...
xm am(mod pm) am(mod pm)
xm+1 b1(mod pm+1) b1(mod pm+1)
...
xm+n bn(mod pm+n), bn(mod pm+n),
ahol bi pi valamely maradékosztálya, bi és bj nem feltétlenül különböző számok, bn<pm+n és bn az n-edik olyan természetes szám, amely nem elégít ki p1-től pm-ig egy kongruenciát sem, pm nem az m-edik prím és p1<p2<...<pm+n itt sem szükséges feltétel, és itt sem szükséges minden prímet felhasználni.
1. Van-e több megoldás?
(Szerintem nincs a jonas által [3239]-ben ismertetett okok miatt.)
Nevezzünk részleges lefedőrendszernek egy olyan kongruenciarendszert, ahol létezik k természetes szám, hogy a k-nál nagyobb természetes számok mindegyike kielégít valamely kongruenciát, azaz k fölött a rendszer minden számot lefed.
2. Konstruálható-e véges, vagy végtelen részleges inkongruens lefedőrendszer, ha minden modulus prím?
3. Konstruálható-e véges, vagy végtelen részleges lefedőrendszer, ha minden modulus prím, és minden prímet kétszer használunk fel?
Elnézést, ha bárkit is untatok.
|
| Előzmény: [3241] bily71, 2010-02-12 22:53:59 |
|
|
|
|
|
| [3239] jonas | 2010-02-12 21:57:23 |
 Nyilván nem, mert a modulusok relatív prímek, így mindegyik sorozat tagjaihoz egyet hozzáadva a kapott sorozatoknak van metszetük, és az ebben lévő számok egyik eredeti sorozatban sincs benne.
|
| Előzmény: [3238] bily71, 2010-02-12 21:01:37 |
|
| [3238] bily71 | 2010-02-12 21:01:37 |
 Konstruálható-e inkongruens lefedőrendszer csak prím modulusú tagokból?
|
|
|
|
| [3235] Sirpi | 2010-02-11 18:03:18 |
 m2mm úgy érti, hogy a bizonyítás ilyen hosszúságban elmondható (gyakorlatilag változatlan formában) úgy, hogy nem ejted ki azt a szót, hogy latin négyzet. Mellesleg én is ezt a bizonyítást ismerem a tétel "alap" bizonyításának.
|
| Előzmény: [3234] bily71, 2010-02-11 17:28:19 |
|
| [3234] bily71 | 2010-02-11 17:28:19 |
 Annyi köze van a latin négyzetekhez, hogy ha nem latin négyzetekről lenne szó, akkor nem biztos, hogy tudnánk párokat képezni, ugyanis nem lenne biztosított, hogy minden sorban szerepeljen az egyes, főleg, hogy csak egyszer, biztosítva a párok egyértelműségét, elvégre definíció szerint egy n×n-es latin négyzet az 1-től n-ig terjedő egész számokat tartalmazza úgy, hogy minden sorában és oszlopában egy szám csak egyszer szerepel.
|
| Előzmény: [3233] m2mm, 2010-02-11 14:52:08 |
|
| [3233] m2mm | 2010-02-11 14:52:08 |
 Ez korrekt megoldás, de ennek valójában semmi köze a latin négyzetekhez. Egyszerűen párokat képezel, ez az egyik legismertebb bizonyítása a tételnek.
|
| Előzmény: [3231] bily71, 2010-02-11 12:49:08 |
|
|
| [3231] bily71 | 2010-02-11 12:49:08 |
 Ha életedben nem hallottad, hogy a latin négyzetek segítségével a Wilson-tétel bizonyítható, ez bizonyára érdekes lesz számodra, és legalább nem "halál ismert", legalábbis általad, (itt most az idézőjel nem iróniát, hanem tényleges idézést jelöl).
Legyen p P, azaz prím. Képezzünk p maradékosztályaiból, a 0-át kihagyva szorzótáblát. Ekkor a táblázat latin négyzet, ezt már [3187]-ben beláttuk. P, azaz prím. Képezzünk p maradékosztályaiból, a 0-át kihagyva szorzótáblát. Ekkor a táblázat latin négyzet, ezt már [3187]-ben beláttuk.
Ennek az a következménye, hogy minden a-hoz létezik egy, és csakis egy b szám, hogy
ab 1(mod p), 1(mod p),
ahol a és b p egy-egy maradékosztálya.
Az a=b csak a=1, vagy a=p-1 esetén fordulhat elő, minden más esetben a b, ugyanis, ha b, ugyanis, ha
a2 1(mod p), 1(mod p),
akkor
a2-1 0(mod p), 0(mod p),
de akkor p nem lehet prím, mert
a2-1=(a-1)(a+1) 0(mod p). 0(mod p).
Ennek az a következménye, hogy az 1<a<p-1 maradékosztályok párokba rendezhetőek, így lesz 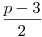 darab olyan számpárunk, hogy darab olyan számpárunk, hogy
aibj 1(mod p). 1(mod p).
Ezeket a számpárokat helyettesíthetjük 1-gyel, így a következőt kapjuk:
(p-1)!=1.2.3...(p-3)(p-2)(p-1)=1.1...1.1(p-1) p-1(mod p). p-1(mod p).
Q.E.D.
|
| Előzmény: [3186] Róbert Gida, 2010-02-01 17:11:09 |
|
|




 (-1)(p-1)/2 (mod p) kongruencia akkor teljesül, ha (p-1)/2 páratlan, azaz p 4k+3 alakú.
(-1)(p-1)/2 (mod p) kongruencia akkor teljesül, ha (p-1)/2 páratlan, azaz p 4k+3 alakú. 


 0 vagy
0 vagy  0, akkor az
0, akkor az 


 P, azaz prím. Képezzünk p maradékosztályaiból, a 0-át kihagyva szorzótáblát. Ekkor a táblázat latin négyzet, ezt már [3187]-ben beláttuk.
P, azaz prím. Képezzünk p maradékosztályaiból, a 0-át kihagyva szorzótáblát. Ekkor a táblázat latin négyzet, ezt már [3187]-ben beláttuk.  b, ugyanis, ha
b, ugyanis, ha