| [3406] robertgidatestvere | 2010-12-31 12:52:39 |
 Igen, de nem az volt a kérdés, hogy te mit csinálsz a gépeden, van aki beszél a számítógéphez, és egy hangfelismerő program írja a szöveget a képernyőre.
A precedencia pedig igenis fontos, számomra egy program bizonyítja egyértelműen, hogy az a precedencia amit kívánsz az tényleg igaz. 2+3*4-et egy matekprogram sem fog 20-ként kiértékelni.
|
| Előzmény: [3404] patba, 2010-12-31 12:43:32 |
|
| [3405] Tassy Gergely | 2010-12-31 12:48:41 |
 Valóban nem a programozási részére gondoltam, a 99!!!!!!!! elméletben kiszámítható ,,kézzel'' is. Persze vizsgálhatjuk azt a változatot is, ahol két !-jel nem állhat egymás mellett.
|
| Előzmény: [3404] patba, 2010-12-31 12:43:32 |
|
| [3404] patba | 2010-12-31 12:43:32 |
 Olvasd el még egyszer a feladatot!(Írni én kézzel szoktam, számítógépen meg gépelni.) Nem programozási feladat, a pontosítás szerintem csak annak szólt, hogy végtelen jelet ne használjunk, meg hasonlóakat.
Az én tippem: 99!!!!!!!!
|
| Előzmény: [3403] robertgidatestvere, 2010-12-31 12:37:34 |
|
| [3403] robertgidatestvere | 2010-12-31 12:37:34 |
 Az ötlet jó, de több probléma is van vele. Először egy olyan már létező programot kéne mutatni, amivel az adott kifejezés (elméletben) kiszámítható volna, és annyi lenne amit mondasz (plusz feltétel persze, hogy pozitív egésznek kell lennie a számnak).
Nekem már a precedencia sem világos, hogy ! vagy ^ van előrébb, bár ez programfüggőnek tűnik.
Ha PARI-GP-re gondoltál, akkor az bukta, mert a ^ jel nélkül ezt nem tudod bevinni, de egyébként sem müködne, mert itt például 2^3!=64 és nem 8!=40320. Mathematica 5.1-ben már n!!-t is multifaktoriálisként értelmezi, így ez már itt elbukik. Maple 12-ben rákérdez n!! esetén, hogy dupla faktoriálist kérsz, vagy a faktoriálist kétszer alkalmazva. De n!!! esetén nekem soha nem alkalmazza a faktoriálist háromszor. Így ez is bukta.
|
| Előzmény: [3402] patba, 2010-12-31 11:44:39 |
|
|
|
| [3400] Tassy Gergely | 2010-12-30 23:29:00 |
 519. feladat. Melyik a 10 karakterrel leírható legnagyobb pozitív egész szám?
(A feladat további pontosításra szorul, egyelőre csak gondolatébresztőnek szántam. Karakter alatt elsősorban a számjegyeket, az alapműveleti jeleket, valamint szükség esetén további, egy számítógép-billentyűzeten megtalálható betűket, szimbólumokat (pl. e, !) értek. Várom az esetleges további felmerülő kérdéseket, ötleteket.)
|
|
|
| [3398] ibiro | 2010-12-29 22:20:00 |
 Tényleg jó az oldal, kösz szépen. Amit ott láttam nem matematikai megoldás, tehát akit érdekel érdemes valami matematikai megoldást is keresni.
|
| Előzmény: [3397] Tóbi, 2010-12-29 01:37:14 |
|
| [3397] Tóbi | 2010-12-29 01:37:14 |
 Kiszámítottam az első pár tagot, arra rákerestem, ezen az oldalon, ahol a nevezetes egész sorozatokat tartják számon. Itt van minden hivatkozás a sorozattal kapcsolatban, utána lehet nézni, ha érdekel. Egyébként valóban csak az első 43 tag egész, utána egyik sem az. Szerintem nagyon hasznos a fenti adatbázis, sokat segített volna a Kömalban is, de sajnos csak az egyetemen hallottam róla először.
|
| Előzmény: [3396] ibiro, 2010-12-28 23:03:29 |
|
|
|
|
| [3393] jonas | 2010-12-10 19:27:40 |
 Az 511-re lényegében jó a válaszod, de csak akkor ez a képlet, ha m+n páros, különben hm,n=0.
Az 512-re jó a válaszod, a tanulság pedig az, hogy ha csak az 511-re adott képletet látnád, akkor sokkal nehezebb lenne megkapni a determinánst, mint így.
Az 513-ra vagy nem egészen jó a megoldásod, vagy a feladatot adtam fel rosszul, mert nem csupa nullák vannak a szorzatban.
|
| Előzmény: [3392] stray dog, 2010-12-10 13:13:34 |
|
|
|
| [3390] apci | 2010-12-09 21:22:52 |
 Sziasztok! Ezzel a feladattal nem boldogulok:
|
 |
|
| [3389] Tóbi | 2010-12-07 22:25:50 |
 Először is egy átfordítás nem hozhat létre kört, és amíg nincs kör, mindig lesz átfordítható csúcs. Tehát a folyamat végtelen sokáig fog tartani. Azt kellene igazolni, hogy minden csúcs végtelen sokszor átfordul. Ekkor Mariska néni eljuthat K-ból A-ba: kinéz egy tetszőleges irányítatlan K-A utat, és átmegy az egyes éleken, mikor azok a megfelelő irányba fordulnak. Tekintsünk egy minimális csúcsszámú gráfot, ahol az állítás nem igaz. Tegyük fel, hogy P olyan csúcs, ami csak véges sokszor fordul át. Ekkor egy idő után P már nem forog, és a P-ből kimenő élek száma monoton nő. Egy idő után ez is megáll. Hasonló igaz a P-ből elérhető pontokra, majd az azokból elérhetőekre is stb. Az elérhető csúcsok halmaza legyen S. Ha V(G)=S akkor egy idő után nem lenne több átfordulás, ez kizárt. Tehát néhány pont kimarad, egy idő után ezek közt zajlana minden átfordulás, mégpedig az S-el nem szomszédosak közt. Tekintsük most a V(G)\S csúcsai által adott részgráfot, és legyen ebben P' egy S-sel szomszédos pont (ilyen létezik az összefüggőség miatt). Ez egy kisebb ellenpélda lenne az állításra.
|
| Előzmény: [3385] Fálesz Mihály, 2010-12-07 12:48:40 |
|
|
|
| [3386] Sirpi | 2010-12-07 13:20:04 |
 Nagyon jó a megfogalmazás :-)
Csak lehet, hogy valamit félreértek, mert túl könnyűnek tűnik ellenpéldát gyártani:
Legyen 3 város, A, B és C, és a kezdeti kétirányú (összefüggő) úthálózat álljon az AB és BC utakból (Mariska néni A-ban lakik, C-be akar eljutni). A kezdeti irányítás legyen C->B->A, ez Mariska néninek nyilván nem fog tetszeni. Erre CB-t megfordítják: C<-B->A, de ekkor B lesz forrás, így CB-t megint megfordítják: C->B->A s.í.t., Mariska néni pedig hoppon marad (persze ha másodszor nem CB-t, hanem BA-t fordítjuk meg, akkor meg is van a kívánt út, szóval meg lehet oldani, hogy eljusson, de azt is, hogy ne).
Ja, és ez nem csak 3 városra ellenpélda, mert nyilván ha B-be becsatlakozik még egy csomó másik út, mondjuk mind B-ből kifelé, akkor is ugyanezt el lehet mondani).
|
| Előzmény: [3385] Fálesz Mihály, 2010-12-07 12:48:40 |
|
| [3385] Fálesz Mihály | 2010-12-07 12:48:40 |
 516. feladat (Valamikor réges-régen, egy nem annyira távoli galaxisban, olimpiai előkészítőn volt.)
Bergengóciában olyan az úthálózat, hogy a városok közötti utak nem ágaznak el, minden út két várost köt össze. Az úthálózat összefüggő, vagyis az utakon bármelyik városból bármelyik városba el lehetett jutni --- legalábbis a múlt hétig. A világgazdasági válság miatt ugyanis a bergengóc kormány változatos megszorításokra kényszerült. Az Utazásról Leszoktató Minisztérium például a következőket rendelte el:
56789/2010. Min. rendelet a helyváltoztatás szabadságának megőrzéséről és védelméről
1.§ (a) Az ország mindegyik útját egyirányúsítani kell.
(b) Az utak irányítását olyan módon kell megválasztani, hogy ne lehessen körbe utazni több város között.
Az intézkedés bevezetése ellen hevesen tiltakoztak a kukutyiniak, mert hozzájuk minden út befelé vezetett, és emiatt sehova nem tudtak utazni. A demonstráció vezérszónoka Mariska néni volt, aki az unokahúga nagybátya sógorának a régi kollégiumi szobatárását szerette volna meglátogatni Alsómocsoládon. A tiltakozások eredményeként a minisztérium a következővel egészítette ki a rendeletet:
2.§ (a) Minden héten, ha van olyan város, ahonnan csak kifelé vezet út, akkor ezek közül ki kell választani az egyiket, és az innen kifelé vezető utak irányítását meg kell fordítani.
(b) Az (a) pont rendelkezéseiben előírtaktól eltekintve, a többi út irányítása nem változik.
Eljuthat-e Mariska néni Kukutyinból Alsómocsoládra?
|
|
| [3384] Tóbi | 2010-12-01 02:43:46 |
 Tényleg van explicit megoldás. Ha k lehetséges végkimenetel van, a idegen egymástól függetlenül a szelvényt vesz, mi pedig k darabot, akkor a nyereményünk várható összege  jelöléssel: jelöléssel:
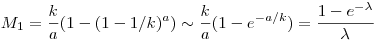
ha különböző szelvényeket veszünk,
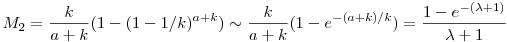
ha véletlenszerűen töltjük ki a szelvényeket.
|
| Előzmény: [3383] Róbert Gida, 2010-11-30 21:22:46 |
|
|
| [3382] Róbert Gida | 2010-11-30 21:20:15 |
 Itt szerintem neked feltételes valószínűséget kéne számolnod, ha összesen k darab telitalálat volt, akkor mennyi a valószínűsége, hogy ebből nekünk n darab telitalálatunk volt (persze 0 n n k). Amit te csinálsz a második szummában sehol nem jelenik meg k a valószínűségben, mást számolsz. k). Amit te csinálsz a második szummában sehol nem jelenik meg k a valószínűségben, mást számolsz.
Az, hogy rossz, legkönnyebben úgy látod: b=k azaz, ha minden szelvény telitalálatos, ekkor persze csak az lehet, hogy az összes szelvényünk nyert, ami a te formuládból nem következik.
Egyszerűbb egyébként úgy számolni, hogy k1 darab telitalálat volt a 8 millió szelvényből, és k2 darab volt nekünk (dupla szumma lesz itt is). Tóbi megoldása mindenesetre szellemesebb és rövidebb.
|
| Előzmény: [3381] Füge, 2010-11-30 18:12:07 |
|






 n
n 1, n
1, n N.
N. 




 n
n