 Úgy látszik, nem lett annyira érdekes a feladat. Akkor megmutatnék egy megoldást.
Az 1.)-re Jonas példája rendben van.
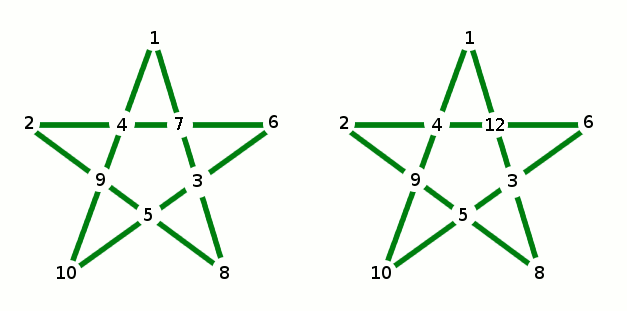
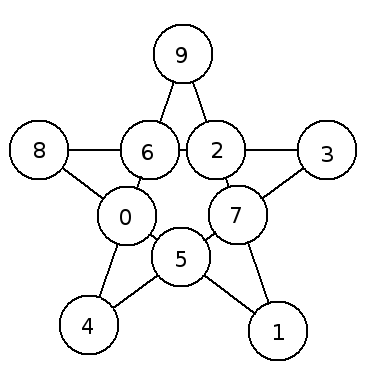
A 2.)-ra azt fogjuk megmutatni, hogy nem lehetséges, hogy 11 egymást követő egész szám közül ki lehet választani 10 különbözőt, úgy, hogy azokkal kitölthető jól a bűvös ötszög.
Indirekt tegyük fel, hogy ilyen kiválasztás, és elrendezés lehetséges. Nyilván akkor lehetséges az is, hogy az 1,2,...,10,11 számok közül hagyunk el egyet, és a maradék 10 számmal töltjük ki a bűvös ötszöget. Legyen V: a vonalakon szereplő 4-4 szám összege, míg S: az ötszögben szereplő 10 szám összege.
Mivel minden az ötszögben szereplő szám két vonalon szerepel 2S=5V 5|2S 5|2S 5|S 5|S
Mivel S=1+2+...10+11-"a hiányzó szám"=66-"a hiányzó szám", ezért "a hiányzó szám" csak az 1,6,11 közül kerülhet ki. Ha az 1-t, vagy a 11-t választjuk, akkor Lórántfy 3605-s feladatát kapjuk (az hasonlóan, ahogy most fogunk dolgozni megmutatható, hogy nem teljesíthető!), így válasszuk kimaradónak a 6-t!
Vagyis most S=66-6=60 , és így V=2S/5=24.
V=24, ami 3-mal osztható. Vagyis minden vonalon a 4 szám összegének 3-mal oszthatónak kell lennie! Most csoportosítsuk a 10 ötszögbe került számunkat a 3-as maradékaik szerint! 2db 0 maradékot ad (3,9), 4 darab 1 maradékot ad (1,4,7,10), és 4 darab 2 maradékot ad (2,5,8,11) 3-mal osztva. A 3-asra, és a 9-re fogunk figyelni!
Bármely két vonalnak egyértelműen létezik metszéspontja, így az ötszögbe került bármely két A,B számhoz (akár egy vonalon vannak, akár nem) van legalább egy harmadik olyan C szám, mellyel mindketten egy vonalon vannak (hiszen minden számra pontosan két vonal illeszkedik, azaz A,B-nek létezik legalább egy-egy nem közös vonala), méghozzá úgy, hogy A,B,C nincs mind egy közös vonalon.
Legyen A=3, B=9, és vizsgáljuk C-t! Mivel C nem osztható 3-mal 1,vagy 2 maradékot ad.
Legyen most C 1 maradékot adó. Az A,C vonalon lévő két másik szám is 1-1 maradékot kell adjon 3-mal osztva (mivel egyik sem adhat 0 maradékot, hiszen B más vonalon van)! Hasonlóan a B,C vonalon lévő másik két szám is 1 maradékot kell adjon! Igen ám, de akkor C, az A,C vonal két másik száma, illetve a B,C vonal két másik száma, azaz 5 különböző szám ad 3-mal osztva 1 maradékot, ami lehetetlen! (Ha abból indulunk ki, hogy C 2 maradékot ad, akkor pedig 5 darab 2 maradékot adó különböző számunk lenne!)
Ellentmondáshoz jutottunk, vagyis valóban lehetetlen a feltételeknek megfelelő bűvös ötszöget csinálni.
|




 =a) :)
=a) :)

 5|2S
5|2S


 cn.tr(A2)
cn.tr(A2)
 2-re valós Hilbert-térként gondolsz, a "szokásos" skaláris szorzattal. E skaláris szorzat által indukált normát jelöljük a szokásos módon ||.||2-vel. Egy x sorozat esetén az n-edik komponensét xn jelölje.
2-re valós Hilbert-térként gondolsz, a "szokásos" skaláris szorzattal. E skaláris szorzat által indukált normát jelöljük a szokásos módon ||.||2-vel. Egy x sorozat esetén az n-edik komponensét xn jelölje.  S.
S. 
 esetén
esetén