| [3658] w | 2013-01-31 19:21:02 |
 Minden bizonnyal a Te megoldásod a legelegánsabb, mert direkt úton visszavezeti a teljes négyzet-egyenlőtlenségre. Helyette próbáld a közepek közötti egyenlőtlenségekkel igazolni a feladatot (természetesebb is az adható megoldás).
Persze rendezési tétellel azonnal látszik ennek a megoldása, de nem működik az általános verzióra határértékek nélkül.
|
| Előzmény: [3653] ibiro, 2013-01-31 13:48:15 |
|
| [3657] w | 2013-01-31 19:16:02 |
 Lehet, hogy van rá egyszerűbb okoskodás, de az utolsó négy számjegyet a hatványok utolsó n számjegyének periodikus ismétlődésével meghatározhatjuk (ezt a 4545-re használjuk, az 5454 meg számológéppel megadható).
|
| Előzmény: [3654] Hajba Károly, 2013-01-31 17:14:38 |
|
|
|
|
| [3653] ibiro | 2013-01-31 13:48:15 |
 Kezdetnek nem rossz, de engem legalábbis nem visz közelebb az általánosabb megoldáshoz, megszorozzuk 4-el mindkét oldalt majd ilyen alakba lehet írni : 2(a2-bc)2+2(b2-ac)2+2(c2-ab)2+(a2-b2)2+(b2-c2)2+(c2-a2)2>=0
|
| Előzmény: [3652] w, 2013-01-30 17:26:13 |
|
| [3652] w | 2013-01-30 17:26:13 |
 Kezdésképpen igazoljuk, hogy
a4+b4+c4 a2bc+b2ca+c2ab. a2bc+b2ca+c2ab.
|
|
|
| [3650] ibiro | 2013-01-30 13:30:19 |
 A "tetszőleges xi>0, si valós számokra" kifejezés azt jelenti hogy si>0 ??? Ha igen akkor lehet gondolkozni a feladaton, ha pedig lehetnek negatív számok is, akkor nem igaz az egyenlőtlenség: n=2, x1=1, x2=2, s1=2,s2=-1 .
|
| Előzmény: [3649] w, 2013-01-13 21:25:23 |
|
| [3649] w | 2013-01-13 21:25:23 |
 Mutassuk meg, hogy tetszőleges xi>0, si valós számokra fennáll (i=1, 2, ..., n):
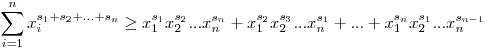 . .
|
|
| [3648] ibiro | 2012-12-08 22:26:04 |
 Az algoritmus remek és tényleg megérti egy hetedikes is, de biztos nem igy kapjuk meg a legkevesebb számú lépést (12,36,324,26244,26243,...,2012) és az algoritmus szerint ez az egyetlen megoldás, a valóságban pedig több is van.
|
| Előzmény: [3647] w, 2012-12-08 21:14:42 |
|
| [3647] w | 2012-12-08 21:14:42 |
 Mi választjuk-e meg a-t és b-t?
Erre egy trviális algoritmus: páros n=2k-ból k2 képezhető, ahol k2>2k, ha (k-1)2>1, k>2, n>4; páratlan n=2k+1-ből k(k+1) képezhető, itt k(k+1)=k2+k>2k+1, ha 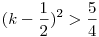 , , 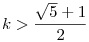 , , 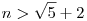 . Tehát szig. mon. növ. sorozatot képezhetünk n0>4 esetén, végül n=n-1+1 -ből n-1 képezhető, elég nagy sorozattag választásával így lecsökkenthetünk a szükséges számra. N>4-re tetszőleges M elérhető, de az is látszik, hogy N . Tehát szig. mon. növ. sorozatot képezhetünk n0>4 esetén, végül n=n-1+1 -ből n-1 képezhető, elég nagy sorozattag választásával így lecsökkenthetünk a szükséges számra. N>4-re tetszőleges M elérhető, de az is látszik, hogy N 4 esetén csak M 4 esetén csak M N érhető el. N érhető el.
Ilyen módon ez könnyen hetedikes szint. A megoldások és lépések minimális száma nem ilyen egyszerű, finoman fogalmazva.
|
| Előzmény: [3645] ibiro, 2012-12-08 11:45:22 |
|
| [3646] w | 2012-12-08 20:48:35 |
 Prímszám-e: 4545+5454?
|
|
| [3645] ibiro | 2012-12-08 11:45:22 |
 "Ha az n természetes számot felirjuk n=a+b alakba (ahol a,b szintén természetes szám), akkor helyettesitjük n-t az ab szorzattal és folytassuk az eljárást. Elindulva 12-vel, eljutunk-e 2012-ig ?". Én ismerek két megoldást (próbálkozással), de vajon hány megoldása van a feladatnak és átalánosan. ha elindulunk N-től eljutunk-e M-ig ? Minimálisan hány lépésben ? Megjegyzem, az eredeti feladat VII. osztályosoknak volt feladva.
|
|
| [3644] Róbert Gida | 2012-12-01 00:10:20 |
 "Az ellenpéldádtól csak úgy szabadulok meg ha még hozzáadom "a és b természetes számok és ab>1"."
Akkor az a=1;b=3-at mondom ellenpéldának. De, hogy valamit mondjak is: a,b>1-et célszerű feltenni, és akkor már igaz lesz az állításod (valamivel kevesebb is elég, de nem lényeges). Wilson tételből jön ki:
(p-1)! -1mod p, ha p prím. Az is igaz, hogy összetett n-re: (n-1)! -1mod p, ha p prím. Az is igaz, hogy összetett n-re: (n-1)! 0mod n, kivéve, ha n=4, ez jelent is egy külön esetet majd a feladatban. 0mod n, kivéve, ha n=4, ez jelent is egy külön esetet majd a feladatban.
|
| Előzmény: [3643] ibiro, 2012-11-30 21:25:20 |
|
| [3643] ibiro | 2012-11-30 21:25:20 |
 Ismét igazad van. Az ellenpéldádtól csak úgy szabadulok meg ha még hozzáadom "a és b természetes számok és ab>1". Bevallom, az eredeti tételt én írtam át a és b formába, de ezek szerint nem figyeltem oda eléggé és eltorzult a dolog. Ime itt az eredeti: "Let p and p+k be positive integers, with (p, p+k) = 1. Then: p and p+k are both prime iff (p-1)!(p+k) + (p+k-1)!p + 2p+k is congruent to 0 (mod p(p+k))". Sajnos innen is kihagyták hogy p>=1 és k>0. Az is igaz hogy (mod 1)-et csak ellenpéldáknál szokták használni ! Azért érdekesnek tartom most is ezt a tételt.
|
| Előzmény: [3641] Róbert Gida, 2012-11-29 18:17:51 |
|
|
|
|
|
|
| [3637] ibiro | 2012-11-27 11:01:11 |
 Csak azt akartam hangsúlyozni, hogy a "nehézség", "hazugság", "szépség",... relatív fogalmak. Az eredeti feladatot egy fórumon találtam VI.osztályosoknak, ezek szerint hibásan volt feltéve,de ... ez egy újabb kihívás. A net-en keresgéltem és valami ilyent találtam: " a és b egyidejűleg prím akkor és csakis akkor ha (a-1)!b+(b-1)!a+a+b  0 (mod ab)". Ekkor gondoltam hogy a feladat nem VI.-nak való. 0 (mod ab)". Ekkor gondoltam hogy a feladat nem VI.-nak való.
|
| Előzmény: [3633] w, 2012-11-26 19:19:32 |
|
|
|
|





 a2bc+b2ca+c2ab.
a2bc+b2ca+c2ab. 4 esetén csak M
4 esetén csak M
 -1mod p, ha p prím. Az is igaz, hogy összetett n-re: (n-1)!
-1mod p, ha p prím. Az is igaz, hogy összetett n-re: (n-1)!