| [368] syllabus | 2004-05-25 23:26:31 |
 Kedves László!
Azért kérdeztem, mert ha meg tudjuk a fentet és a lentet különböztetni, akkor ha 3-1 után ellentétest fogunk meg, akkor már egy lépésben kinyithatjuk a zárat.
|
|
| [367] Csimby | 2004-05-25 22:53:41 |
 Onogur, nem mondom még meg a megoldást, hátha valaki kitalálja (egyébként én csak olyat ismerek ami az első 1 millió tagra bizonyítja, hogy nincsen benne csak 3 négyzetszám, de szerintem azzal a módszerrel meglehet csinálni teljesen (még nem tettem meg, tehát gonosz dolog volt kitűzni a példát), ráadásul amit ismerek megoldást az is csak algoritmus, de hát vannak itt nálam okosabbak akik majd kitalálják ;-)) Segítség: A sorozat különböző mod.-al vett maradékait kell vizsgálni és így egy csomó kiesik (hiszen minden mod.-ra megvan, hogy mely maradékok nem tartozhatnak négyzetszámokhoz.)
|
| Előzmény: [362] Hajba Károly, 2004-05-24 23:58:07 |
|
| [366] lorantfy | 2004-05-25 22:15:53 |
 Kedves Károly!
Kösz az infót! Nem fogtam fel első olvasásra ezt a magában álló kapcsolót, hát hozzáköltöttem egy lámpát. Igy persze túl egyszerű lenne.
81. feladathoz: Szerintem nem lényeges, hogy le vagy fel vannak kapcsolva a kapcsolók, mert azt írja: a zár akkor nyit, ha mindegyik kapcsoló azonos állásban van.
|
| Előzmény: [364] Hajba Károly, 2004-05-25 10:07:53 |
|
| [365] syllabus | 2004-05-25 21:36:12 |
 Azt szeretném kérdezni a 81-es feladathoz, hogy mikor megfogunk két kapcsolót akkor azt érezzük, hogy különböző állásban vannak, vagy azt, hogy az egyik "fel" van kapcsolva a másik "le"?
A feladat tehát arra megy ki, hogy véges algoritmust adjunk, vagy egy elég sok lépésben "nagyon valószínű" eljárást keresünk?
|
|
| [364] Hajba Károly | 2004-05-25 10:07:53 |
 Kedves László!
Újrafelbukkant Gyuri szellemes feladatain én is elgondolkoztam.
A 81. feladatnál szerintem nem lehet 100 % biztonságú stratégiát kialakítani, de még gondolkodom rajta. A 82. feladatot pedig ismerem. Itt a kapcsoló csak egy állapotot mutat, de nem égőt kapcsol, így egy rab csak akkor jut újabb infóhoz, ha éppen ő van kinn sétán és megnézi a kapcsoló aktuális állapotát.
HK
|
| Előzmény: [363] lorantfy, 2004-05-25 09:31:53 |
|
| [363] lorantfy | 2004-05-25 09:31:53 |
 Kedves Gyuri!
Örülök, hogy újra látunk itt a Fórumon és a két jó példának is.
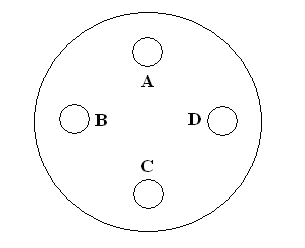
81. feladathoz: Két lyukat választhatunk ki. Vagy szomszédosakat választunk: pl.A-B, vagy átlósan kettőt: pl. A-C. Két kiválasztás után 3 kapcsolót biztos azonos állásba tudunk állítani, legyen ez a 3 A-B-C. Ha a D kapcsoló is ebben az állásban van, akkor a zár kinyílik.
Ha nem, akkor tudjuk hogy D ellenkező állásban van.
Ezután a következő a taktika: Kiválasztunk két lyukat, de csak akkor váltjuk át az egyik kapcsolót, ha ellenkező kapcsoló állást tapasztalunk. Ha a D kapcsolót váltottuk át, a zár kinyílik, ha nem akkor két-két kapsoló azonos állásban fog állni, pl. A és D 1-es, B és C 0 állásban.
Ezután viszont csak akkor fogjuk mindkét kiválasztott kapcsolót átváltani, ha azonos a kapcsoló állás. Ekkor a zár kinyílik.
Egyetlen apró kérdés maradt: Lehetséges-e ezt véges lépésben elvégezni?
82. feladathoz: A megbeszélésen minden rab kapjon egy sorszámot, amit megjegyez és megjegyzi még azt is, mi az utolsó sorszám. A cella falára mindegyik felkarcol egy táblázatot, annyi oszloppal ahányan vannak. Az éppen kint lévő rab annyiszor kapcsolja fel és le a lámpát, amennyi a sorszáma. Ekkor a cellában lévők tesznek egy x-et a megfelelő oszlopba, Ő meg a saját oszlopába, mikor visszaviszik. Ha bármelyik rabnál minden oszlopban lesz legalább egy x, akkor szólhat, hogy kész.
|
 |
| Előzmény: [361] Gyuri, 2004-05-24 14:08:19 |
|
| [362] Hajba Károly | 2004-05-24 23:58:07 |
 A 80. feladathoz:
A Fibonacci-számok birodalmába vezet a matematika.lap.hu oldalon található "ugródeszka" - aljas link :o)
Pl.: Fib(300)-ig nincs négyzetszám, de van néhány prím; találtam egy képletet, de nem sokra mentem vele:
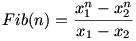 ahol x1 és x2 a x2-x-1=0 egyenlet gyökei. ahol x1 és x2 a x2-x-1=0 egyenlet gyökei.
HK
|
| Előzmény: [359] Csimby, 2004-05-23 22:59:42 |
|
| [361] Gyuri | 2004-05-24 14:08:19 |
 Kedves Mindenki!
A mostani feladatokkal még nem barátkoztam meg, de van két ajándékom.
81.feladat: Egy körlap alakú zárat kell kinyitni. Szimmetrikusan, 4 lyuk található a körlapon. Mindegyik lyukban van egy kétállású kapcsoló, melyek nem látszanak. A zár akkor nyit, ha mindegyik kapcsoló azonos állásban van. A kapcsolók állása viszont kitapintható! Lehetöségünk van kiválasztani két lyukat, majd oda egy-egy kezünkkel benyúlni, majd a kapcsolók kitapintása után azokon állítani. Miután ezt megtettük, a körlap alakú kapcsolótábla forgásnak indul, majd újra megáll. De hogy az eredeti helyzetéhez képest miként, arról semmit nem tudunk, hisz a forgás nagyon gyors volt. Ezután ismét kiválaszthatunk két lyukat, és az elöbb leírt módon operálhatunk. Ismét forgás következik. És így tovább!
Kinyitható-e a zár biztosan? Feltéve persze, hogy nem jelölhetjük meg a lyukakat! Megj.: ábrát nem csináltam, elnézést!
82.feladat: Egy börtönben 100 rab van. Az örök mindennap kiengednek egy rabot sétálni. A választás véletlenszerü. (Ha vki épp tegnap volt kint, attól még ma is kimehet, ilyenfajta megkötések nincsenek.) Megegyeznek a rabokkal, hogy mindenkit elengednek, ha a rabok szólnak, hogy már mindannyian voltak kint legalább 1x sétálni. Viszont a rabok a megegyezés ill. az utána következö stratégia megbeszélése után már nem tudnak egymással kommunikálni. Mindössze 1 kapcsoló van az udvaron, amit kapcsolgathat az éppen kint lévö rab. Tehát tfh. kezdetben a kapcsoló le van kapcsolva. A rabok kitalálták a stratégiát, ezután már az említett módon zajlanak a napok. Mi legyen a strat.? Természetesen ha korábban szólnak, azaz még nem is volt kint mindenki, akkor ugrott az egész. Feltehetö továbbá, h mindenki akárhányszor ki is tud menni, tehát nem halnak meg, meg ilyenek.
Jó fejtörést! (A másodikat még én sem tudom, ma kaptam egy barátomtól.)
|
|
| [360] Hajba Károly | 2004-05-24 01:09:41 |
 Kedves Csimby!
Én eddig 3-at találtam: a0=1;a1=1;a12=144. Az Excell 15 jegy pontosságával a73=806.515.533.049.393-ig nincs újabb. Efölött az Excell már alkalmatlan, programozói gyakorlatom nincs, hogy írjak egy rövid rutint, s általam nem ismert egy Fib(n)=... közvetlen képlet, melyből esetleg lehetne következtetni valamit.
Kiváncsi vagyok a Te megoldásodra is.
HK
|
| Előzmény: [359] Csimby, 2004-05-23 22:59:42 |
|
| [359] Csimby | 2004-05-23 22:59:42 |
 80.feladat Hány négyzetszám van a Fibonacci-sorozatban?
|
|
|
| [357] Kós Géza | 2004-05-17 14:11:17 |
 Mielőtt az Emberevők Szigete végleg elsülyedne a Feledés Tengerében, próbáljuk meg Csimby gondolatait egy teljes megoldássá rendezni.
Az előzést úgy értettem, hogy két falu között az egyik megelőzi a másikat. Tehát U elindul U-ból, és miközben V felé bandukol, megelőzi őt vetélytársa, a konkurrens felekezet tanait terjesztő T is, és V is partra száll V-ben. Mire U odaér V-be, addigra ott már megették T-t, és U mit sem sejtve tovább mehet W-be, ahol ő lesz a menü. Az U tehát U-ból indul, W-ben végzi, és közben mégis elindult valaki V-ből...
Szeretném hangsúlyozni, hogy az előzés lehetőségét példának hoztam fel arra, hogy sok részlet nincs következetesen és pontosan leírva. A teljesen végig nem gondolt részletekben pedig elbújhat egy olyan hiba, ami az egész megoldást megfúrja.
* * *
Térjünk vissza a megoldásra. Osszuk a misszionáriusokat két csoportra. Az egyikbe tartoznak a szerencsétlenebbek, akiket azonnal megesznek. A másik csoport a még szerencsétlenebbek, akiknek előbb dolgozni is kell; az a falu, ahonnan indulnak, az odaérkezésükkor éppen pogány. Minden még szerencsétlenebb misszionárius (MSZM) megtesz egy bizonyos utat a parton.
Csimby megoldása a következő lépésekből állna:
1. Az MSZM-ek által megtett utak nem fedhetik át egymást; nincs olyan partszakasz, ahol két misszionárius is áthaladt;
2. Az MSZM-ek által megtett partszakaszok egymáshoz csatlakoznak és a sziget teljes kerületét pontosan egszer lefedik.
3. Minden egyes faluban összesen két misszionárius fordult meg, és végül a falu újra pogány lett.
|
| Előzmény: [342] Csimby, 2004-04-23 14:09:11 |
|
| [356] joe | 2004-05-15 19:16:15 |
 A 78. feladathoz hasonló, de talán egy kicsit érdekesebb és elegánsabb megoldású a következő:
79. feladat: Tetszőleges n természetes számra állítsuk össze az A és B betűkből az összes lehetséges n betű hosszúságú szót. Osszuk e szavakat két halmazba, Pn-be és Nn-be aszerint, hogy egy adott szóban a BA betűcsoport előfordulásainak száma páros vagy páratlan (a nullát páros számnak tekintjük). Például a BABBBBA szó és az AAAAAAB szó a P7 halmazba, az AABBABB szó és a BABAABA szó az N7 halmazba tartozik. Határozzuk meg, mely n számokra van a Pn és az Nn halmaznak ugyanannyi eleme.
Hogy őszinte legyek, a 78. feladat megoldása nem túl szép, a 79.-re azonban ismerek egy ritka érdekes bizonyítást, ami eltér a "hivatalos" megoldástól és szerintem sokkal szebb.
Ha valaki tudna valamit mondani az ilyen feladatok eredetéről és mélyebb jelentőségéről, azt megköszönném.
|
|
| [355] joe | 2004-05-14 18:49:38 |
 Mint új fórumos, egy feladattal kezdeném:
78. feladat: Tetszőleges n természetes számra állítsuk össze az A és a B betűkből az összes lehetséges n betű hosszúságú "szót". Jelölje pn azon n hosszúságú "szavak" számát, melyek nem tartalmaznak sem négy egymást követő A betűt (AAAA csoportot), sem három egymást követő B betűt (BBB csoportot). Határozzuk meg a következő kifejezés értékét
|
 |
|
| [354] skg | 2004-05-13 19:49:14 |
 Hi!
Régebben beszéltetek itt a bűvös kockáról (rubik) azt szeretném megkérdezni, hogy tudtok-e olyan lapot, ahol van valami róla?
|
|
|
|
|
|
|
| [348] nadorp | 2004-04-27 15:42:14 |
 Megoldás a 77. feladatra.
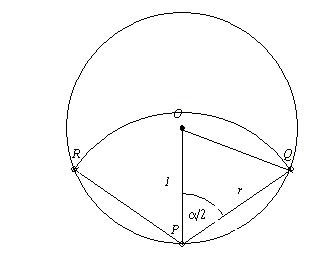
Legyen legelő középppontja O, sugara 1. A karó helye legyen P, a kötél hossza r ( lásd az ábrát). A P középpontú r sugarú kör messe a legelőt a Q és R pontokban.
Legyen RPQ = = . Nyilván . Nyilván  tompaszög, hiszen ellenkező esetben a két körív közti terület nagyobb a legelő felénél és az is látszik, hogy tompaszög, hiszen ellenkező esetben a két körív közti terület nagyobb a legelő felénél és az is látszik, hogy 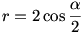 . A két körív közti terület egy körcikkre és két egybevágó körszeletre bontható, a területre: . A két körív közti terület egy körcikkre és két egybevágó körszeletre bontható, a területre:
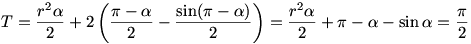
Mivel 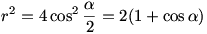 , ezért , ezért
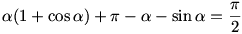
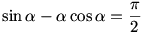
Ezt az egyenletet csak közelítőleg lehet megoldani,  =109,19o körül van.Innen r=1,16 egység. =109,19o körül van.Innen r=1,16 egység.
|
 |
|
| [347] lorantfy | 2004-04-27 12:33:01 |
 Az 59. feladat így szólt: Oldjuk meg a
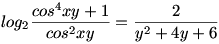
egyenletet, ha (x,y) R2 ! R2 !
Az 59. feladat megoldása: A logaritmus „hasában” álló A kifejezés:
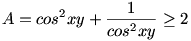
így log2A 1. 1.
A jobb oldali B tört nevezője: y2+4y+6=(y+2)2+2 2, így B 2, így B 1. 1.
A két oldal csak akkor lehet egyenlő, ha log2A=B=1. tehát y = -2. A = 2-ből cos2xy=1. cos2(-2x)=cos2(2x)=1, amiből cos2x=1 vagy cos2x=-1, 2x=k . .
Tehát 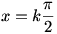 , ahol k , ahol k Z. Z.
|
| Előzmény: [343] Hajba Károly, 2004-04-27 00:15:48 |
|
|
|
| [344] lorantfy | 2004-04-27 10:47:14 |
 A 63. feladat ez volt: Három barátnő főzéshez készül, az egyik 5 db fát, a másik 3 db fát hozzott a spórba és így mindhármójuk megfőzött. A harmadik, mivel nem volt tüzifája, 8 forinttal járult hozzá a tüzifa költségekhez. A másik két barátnő milyen arányban osztozik igazságosan a pénzen?
A 63. feladat megoldása: A harmadik barátnő 8 Ft-ot ad a rá eső 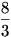 fahasábért, így fahasábért, így 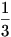 fahasáb 1 Ft-ot ér. fahasáb 1 Ft-ot ér.
Az első barátnő, aki 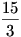 fahasábot adott fahasábot adott 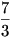 -al adott többet mint a saját része, így 7 Ft-ot kap, míg a második, aki -al adott többet mint a saját része, így 7 Ft-ot kap, míg a második, aki 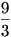 -ot adott csak -ot adott csak 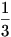 -al adott többet mint a saját része, tehát 1 Ft-ot kap a 8 Ft-ból. -al adott többet mint a saját része, tehát 1 Ft-ot kap a 8 Ft-ból.
|
| Előzmény: [343] Hajba Károly, 2004-04-27 00:15:48 |
|













 =
= . Nyilván
. Nyilván 
 R2 !
R2 !  1.
1.  1.
1.  .
.