|
| [3784] Ali | 2013-09-13 10:38:22 |
 Legyen g(x)=f(x)-x, és gn(x)=g(g(...g(x)...)). Az értelmezési tartományra tett megszorítás miatt g(x) 0 0  x x 0 esetén. 0 esetén.
Megoldva a gn+2(x)+gn+1(x)-2gn(x)=0 másodfokú lineáris rekurziót ( g0(x):=x, g1(x)=g(x) ),
gn(x)=(-2)n[x-g(x)]/3 +[2x+g(x)]/3, n 2 2
Ha x>g(x), akkor elég nagy páratlan n-re, míg x<g(x) esetén elég nagy páros n-re ellentmondás. Így g(x)=x és f(x)=2x.
|
| Előzmény: [3777] w, 2013-09-02 22:15:48 |
|
|
| [3782] juantheron | 2013-09-10 05:54:02 |
 Solution for real a,b,c in
a[a]+c{c}-b{b}=0.16
b[b]+a{a}-c{c}=0.25
c[c]+b{b}-a{a}=0.49
Where [x]= Integer part of x
and {x}= fractional part of x
|
|
| [3781] HoA | 2013-09-04 23:31:16 |
 A :-) -ból sejtem, észrevetted, hogy ez valójában a közismert izogonális pontos megoldás átírva komplexre.
A feladat talán éppen ezért érdekes: Hogyan derül ki a komplex megközelítésből, hogy a módszer csak 120o -nál kisebb szögű háromszögre működik?
|
| Előzmény: [3780] Fálesz Mihály, 2013-09-04 18:44:31 |
|
|
| [3779] HoA | 2013-09-04 10:54:29 |
 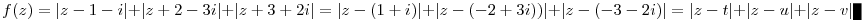 , ahol t=1+i,u=-2+3i,v=-3-2i Legyen továbbá z'=z-u,t'=t-u,v'=v-u . , ahol t=1+i,u=-2+3i,v=-3-2i Legyen továbbá z'=z-u,t'=t-u,v'=v-u . 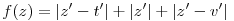 . Felhasználjuk, hogy . Felhasználjuk, hogy 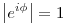 és és  ( ujjgyakorlat ) . Legyen ( ujjgyakorlat ) . Legyen 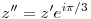 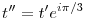 Ekkor Ekkor
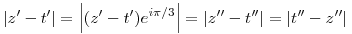
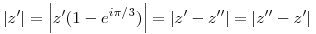
és innen a sokszög egyenlőtlenség miatt
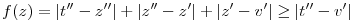
Numerikusan 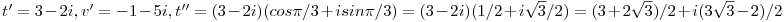 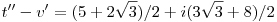 . . 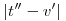 ~ 7,84 ~ 7,84
Feladatnak hagyom annak bzonyítását, hogy létezik is olyan z' - és innen z - érték, melyre f(z) felveszi minimális értékét – például a megfelelő z kiszámításával.
|
| Előzmény: [3775] juantheron, 2013-09-02 21:15:26 |
|
| [3777] w | 2013-09-02 22:15:48 |
 A következő függvényegyenlet leginkább a megoldási módszere miatt hasznos/érdekes 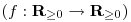 : :
f(f(x)-x)=2x.
|
|
|
| [3774] w | 2013-08-11 16:48:19 |
 Igen. Sok, az előbbihez hasonló feladat generálható. Olyan  szám kell nekünk, melyre az szám kell nekünk, melyre az
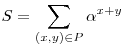 (*) (*)
összeg a lépések során invariáns marad, ahol P jelöli a zsetonok helyeinek halmazát. Az előbbi feladatban  x+y= x+y= (x+1)+y+ (x+1)+y+ x+(y+1)-ra redukálódik a (*) egyenlet, ahol x+(y+1)-ra redukálódik a (*) egyenlet, ahol 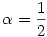 megfelel célunknak. Miért is? Úgy általában, olyan megfelel célunknak. Miért is? Úgy általában, olyan  számra van szükségünk, melyre számra van szükségünk, melyre
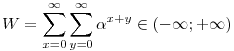 , ,
azaz az első síknegyed súlya véges. Ez éppen   (-1;+1) esetén következik be, és ekkor (-1;+1) esetén következik be, és ekkor
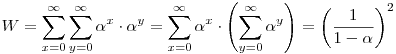
a mértani sor összegzőképlete szerint. A feladatokhoz pedig a P(x) polinomot rendelhetjük, amiről tudjuk, hogy van -1 és +1 között nemnulla gyöke, és tükrözi a zsetonok változását, azaz erre redukálódik a (*) egyenlet egy lépésnyi változás során. A VV-s példában ez a polinom P(x)=2x1-1 volt.
Aki ismer további alkalmazásokat erre a módszerre, örömmel olvasnám azokat.
|
| Előzmény: [3771] Micimackó, 2013-08-07 13:22:20 |
|
|
| [3772] aaaa | 2013-08-07 20:19:50 |
 a) ez ekvivalens n2 darab eredeti feladatbeli (kezdőhelyzet)->(véghelyzet) lehet-e kérdés megválaszolásával.
b) pl. (1;1)-re raksz, erre nem tudod az operációt alkalmazni.
|
| Előzmény: [3770] w, 2013-08-03 14:03:32 |
|
| [3771] Micimackó | 2013-08-07 13:22:20 |
 Megsúlyozzuk a mezőket, hogy egy érme mindig egyet érjen. Így 4 mező van, amiből 2-t akarunk üresen és két érmét akarunk a Fálesz verzióban, így ez nem lehet. A b) résznél még a szélső sorra és oszlopra is figyelni kell, mert ott is marad kis plusz üres terület és így nem lesz elég hely.
|
| Előzmény: [3768] w, 2013-08-02 22:28:38 |
|
| [3770] w | 2013-08-03 14:03:32 |
 Egyetértek, csak az eredeti feladatot akartam kitűzni. Lehetne bőven variálni a dolgokat: keressünk kezdő- és célhelyzeteket az (x,y) (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb. (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb.
Megkérdezném (a feladatot még nem gondoltam át): az (x,y) (x+1,y+1), (x-2,y-1) hasonló változatban legalább hány zsetont kell {(x,y): x,y egész} halmazra rakni, hogy sehogy se lehessen elérni, hogy mondjuk az (1,1)(1,10)(10,10)(10,1) négyzetben ne legyen zseton. (x+1,y+1), (x-2,y-1) hasonló változatban legalább hány zsetont kell {(x,y): x,y egész} halmazra rakni, hogy sehogy se lehessen elérni, hogy mondjuk az (1,1)(1,10)(10,10)(10,1) négyzetben ne legyen zseton.
|
| Előzmény: [3769] Fálesz Mihály, 2013-08-03 05:45:44 |
|
| [3769] Fálesz Mihály | 2013-08-03 05:45:44 |
 Nem értem, hogy az (a) rész miért ennyire bonyolult. Szerintem elég lenne három pont: (0,0), (1,0) és (0,1). Ha kezdetben csak ezeken van zseton, akkor akárhány lépés után is lesz legalább az egyiken.
|
| Előzmény: [3757] w, 2013-07-27 22:52:42 |
|
|
| [3767] Micimackó | 2013-08-02 21:06:06 |
 Nekem úgy tűnik nem lehet, mert nem férnek el. Az első bőven nem fér el (nem is marad elég hely a táblán), a másodikhoz már lenne elég hely, de nincs jól elosztva. Úgyhogy szerintem nem lehet.
|
| Előzmény: [3757] w, 2013-07-27 22:52:42 |
|
|
| [3765] Lóczi Lajos | 2013-08-01 11:04:27 |
 A célkifejezés négyzete azonosan egyenlő a nullára rendezett feltételi egyenletek egy másodfokú polinomjával. A konstans tag 1728-nak adódik, innen egy gyökvonás.
|
| Előzmény: [3762] w, 2013-07-31 12:57:17 |
|
|
|
|
|
|
|




 0
0  x
x

 szám kell nekünk, melyre az
szám kell nekünk, melyre az  (-1;+1) esetén következik be, és ekkor
(-1;+1) esetén következik be, és ekkor 
 (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb.
(x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb. 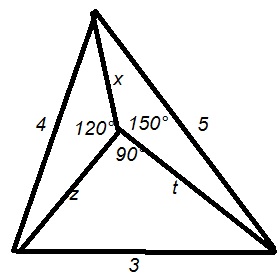

 y2/3+z2=t2+z2=32 Pitagorasz-tétel. A többi már egyértelmű.
y2/3+z2=t2+z2=32 Pitagorasz-tétel. A többi már egyértelmű.