|
|
|
| [3796] Zilberbach | 2013-10-12 19:48:25 |
 Ebben a témában nem tördeli be a túl hosszú sorokat a gépem/programom. Mi lehet az oka?
|
|
| [3795] Sinobi | 2013-10-12 01:30:53 |
 Kaptam egy "érdekes" geometria feladatot, nem tudom mit lehetne vele kezdeni, ami nem kórdináta.
a, Ha van egy e egyenes, és egy p parabola, szerkeszd meg azokat a pontokat a parabolán, amelyek felezőmerőlegese az egyenes. (eddig nem volt nehéz)
b, Bizonyítsd be, hogy ha van egy parabolán három pontpár (húr), amelyek felezőmerőlegesei egy ponton mennek át, akkor ha a hat pontot a parabola tengelyirányában elaffinítjuk, akkor az így kapott pontok felezőmerőlegesei is egy ponton fognak átmenni.
c, Ily módon egy parabola és egy affinitás meghatároz egy  tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy  egyenestartó. egyenestartó.
|
|
| [3793] csábos | 2013-10-11 12:57:17 |
 Kedves HOA!
A probléma Steinerig és Fermat-ig visszavezethető. http://en.wikipedia.org/wiki/Steinertreeproblem Sőt, mér a Gyilkos számok egyik jelenetében is láttam. 2. évad Toxin című rész, 31. perctől. A kérdésem igazából arra vonatkozott, hogy a komplex számos megoldás-felvetés honnan ered. Ami még igazán érdekel: Minél korábbi előfordulása az
x2+xy+y2=a
x2+xz+z2=b
z2+zy+y2=c
típusú feladatnak.
Tud valaki erről valamit?
|
| Előzmény: [3792] HoA, 2013-10-10 16:48:43 |
|
| [3792] HoA | 2013-10-10 16:48:43 |
 Hát igen, mint a Ludas Matyi mottója mondta. „Nincsenek régi viccek, csak öreg emberek. Egy újszülöttnek minden vicc új” Nem emlékszem, hol láttam először, talán valamelyik Reiman könyvben. Most az interneten rákeresve ezt találtam legelőször:
Nemzetközi matematikai diákolimpiák (1959–2003)books.google.hu/books?isbn=9639548049 610 – 611. old.
http://books.google.hu/books?id=nNihkOMB8qYC&pg=PA610&lpg=PA610&dq=izogon%C3%A1lis+pont&source=bl&ots=ocxjZNxUjz&sig=g6aMbTyKXDcQBRh57RTWfDsgGfM&hl=hu&sa=X&ei=Fa5WUoy9HauX5ATV84HIBw&ved=0CGQQ6AEwCw#v=onepage&q=izogon%C3%A1lis%20pont&f=false
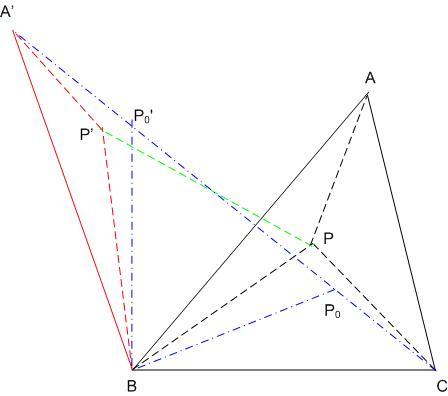
A lényeg: A 120 fokosnál nem nagyobb szögű háromszög síkjának az a pontja, melynek a csúcsoktól mért távolságösszege minimális, az izogonális pont. Bizonyítás: Legyen az ABC háromszög síkjának egy pontja P. Forgassuk el az ABP háromszöget B körül 60 fokal , új helyzete A’BP’ ( A’ az AB egyenes C-t nem tartalmazó oldalán ) . Ekkor A’P’ = AP, BPP’ háromszög szabályos, BP = BP’ = PP’ . A P pont csúcsoktól mért távolságainak összege AP + BP + CP = A’P’ + P’P +PC , vagyis egyenlő az A’P’PC töröttvonal hosszával. Mivel A’ és C helyzete P-től független, ez a hossz akkor a legkisebb, ha ha egybeeseik az A’C szakasszal. A minimális távolságösszeget adó P0 pont ( és 60 fokos elforgatottja , P0’ ) rajta van A’C –n, BP0P0’ szabályos, így BP0C szabályos, így BP0C =120o és BP0’A’ =120o és BP0’A’ =120o miatt BP0A =120o miatt BP0A is 120o is 120o
[3791]-re: Nézd meg, mi a helyzet, ha ABC >120o >120o
|
 |
| Előzmény: [3790] csábos, 2013-10-09 21:17:40 |
|
| [3791] csábos | 2013-10-09 22:21:43 |
 Természetesen a létezés bizonyításánál. Kavics mindig a tanteremben röpködő piros krokodilokkal példálózott. Ha azok léteznek, akkor minden igaz. A konstrukció mindig nehezebb a bizonyításnál. Ha feltesszük, hogy valami van, arról már könnyebb bármit igazolni.
|
| Előzmény: [3781] HoA, 2013-09-04 23:31:16 |
|
|
|
| [3788] HoA | 2013-10-04 22:04:07 |
 Azért írta ki furán, mert a százalék jelet megjegyzés kezdetének veszi, és mindent elhagy, amit a sorban utána írsz . Valamelyik témában nemrég volt szó róla. Tehát így kell írni, hogy látható legyen: \%
A feladattípus elég közismert. Nekem van egy egész kis könyvem belőlük. És persze egy táblázatos módszerrel elég automatikusan megoldható.
Az, hogy az emberek hány %-a képes megoldani, kicsit nézőpont kérdése. Készséggel elhiszem, hogy ha 100 embernek feladod, csak 1-2 -től kapsz megoldást. Nem azért, mert képtelen lenne megoldani, de nem érdekli annyira, hogy végigküzdje. Más lenne a helyzet, ha az élete - na jó, a havi fizetése függne tőle.
|
| Előzmény: [3787] koma, 2013-10-04 20:25:34 |
|
| [3787] koma | 2013-10-04 20:25:34 |
 -De furán írta ki-, szóval állítólag az emberek két százaléka tudja megoldani, és szerintem azért jóval többen képesek lehetnek rá, ti hogyan vélekedtek?
|
| Előzmény: [3786] koma, 2013-10-04 20:22:50 |
|
| [3786] koma | 2013-10-04 20:22:50 |
 Sziasztok, a véleményetekre lennék kíváncsi, szerintem nagyon sokan ismeritek a feladványt:
Ezt a feladatot Einstein írta. Azt mondta, hogy az emberek 98
Tények: 1. 5 ház van, különböző színüek. 2. Minden házban él egy-egy ember, mindegyik más nemzetiségű. 3. Az öt tulajdonos különböző italokat fogyaszt, különféle cigit szív és más-más állatot tart. 4. Nincs két olyan tulajdonos aki ugyanazt az állatot tartaná, ugyanazt a cigit szívná, vagy ugyanazt az italt inná.
1. A brit a piros házban lakik. 2. A svéd kutyát tart. 3. A dán teát iszik. 4. A zöld ház a fehér ház bal oldalán van. 5. A zöld ház tulajdonosa kávét iszik. 6. Az a személy aki Pall Mall-t szív madarat tart. 7. A sárga ház tulajdonosa Dunhill-t szív. 8. Az az ember aki a középső házban lakik tejet iszik. 9. A norvég az első házban lakik. 10. Az ember aki Blend cigit szív amellett lakik aki macskát tart. 11. Az az ember aki lovat tart amellett lakik aki Dunhill cigit szív. 12. A tulaj aki Blue Mastert szív, sört iszik. 13. A német Prince-t szív. 14. A norvég a kék ház mellett lakik. 15. Az ember aki Blend-et szív, a vizet ivó ember szomszédja.
-Én 20-25 perc alatt megoldottam, de nem érzem úgy, hogy a felső 2
|
|
|
| [3784] Ali | 2013-09-13 10:38:22 |
 Legyen g(x)=f(x)-x, és gn(x)=g(g(...g(x)...)). Az értelmezési tartományra tett megszorítás miatt g(x) 0 0  x x 0 esetén. 0 esetén.
Megoldva a gn+2(x)+gn+1(x)-2gn(x)=0 másodfokú lineáris rekurziót ( g0(x):=x, g1(x)=g(x) ),
gn(x)=(-2)n[x-g(x)]/3 +[2x+g(x)]/3, n 2 2
Ha x>g(x), akkor elég nagy páratlan n-re, míg x<g(x) esetén elég nagy páros n-re ellentmondás. Így g(x)=x és f(x)=2x.
|
| Előzmény: [3777] w, 2013-09-02 22:15:48 |
|
|
| [3782] juantheron | 2013-09-10 05:54:02 |
 Solution for real a,b,c in
a[a]+c{c}-b{b}=0.16
b[b]+a{a}-c{c}=0.25
c[c]+b{b}-a{a}=0.49
Where [x]= Integer part of x
and {x}= fractional part of x
|
|
| [3781] HoA | 2013-09-04 23:31:16 |
 A :-) -ból sejtem, észrevetted, hogy ez valójában a közismert izogonális pontos megoldás átírva komplexre.
A feladat talán éppen ezért érdekes: Hogyan derül ki a komplex megközelítésből, hogy a módszer csak 120o -nál kisebb szögű háromszögre működik?
|
| Előzmény: [3780] Fálesz Mihály, 2013-09-04 18:44:31 |
|
|
| [3779] HoA | 2013-09-04 10:54:29 |
 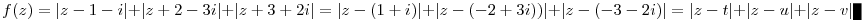 , ahol t=1+i,u=-2+3i,v=-3-2i Legyen továbbá z'=z-u,t'=t-u,v'=v-u . , ahol t=1+i,u=-2+3i,v=-3-2i Legyen továbbá z'=z-u,t'=t-u,v'=v-u . 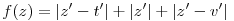 . Felhasználjuk, hogy . Felhasználjuk, hogy 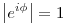 és és  ( ujjgyakorlat ) . Legyen ( ujjgyakorlat ) . Legyen 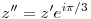 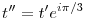 Ekkor Ekkor
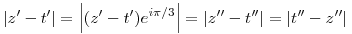
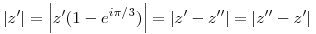
és innen a sokszög egyenlőtlenség miatt
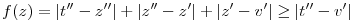
Numerikusan 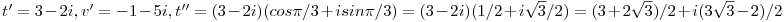 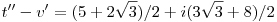 . . 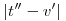 ~ 7,84 ~ 7,84
Feladatnak hagyom annak bzonyítását, hogy létezik is olyan z' - és innen z - érték, melyre f(z) felveszi minimális értékét – például a megfelelő z kiszámításával.
|
| Előzmény: [3775] juantheron, 2013-09-02 21:15:26 |
|
| [3777] w | 2013-09-02 22:15:48 |
 A következő függvényegyenlet leginkább a megoldási módszere miatt hasznos/érdekes 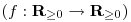 : :
f(f(x)-x)=2x.
|
|
|
| [3774] w | 2013-08-11 16:48:19 |
 Igen. Sok, az előbbihez hasonló feladat generálható. Olyan  szám kell nekünk, melyre az szám kell nekünk, melyre az
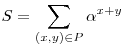 (*) (*)
összeg a lépések során invariáns marad, ahol P jelöli a zsetonok helyeinek halmazát. Az előbbi feladatban  x+y= x+y= (x+1)+y+ (x+1)+y+ x+(y+1)-ra redukálódik a (*) egyenlet, ahol x+(y+1)-ra redukálódik a (*) egyenlet, ahol 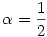 megfelel célunknak. Miért is? Úgy általában, olyan megfelel célunknak. Miért is? Úgy általában, olyan  számra van szükségünk, melyre számra van szükségünk, melyre
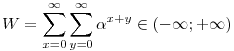 , ,
azaz az első síknegyed súlya véges. Ez éppen   (-1;+1) esetén következik be, és ekkor (-1;+1) esetén következik be, és ekkor
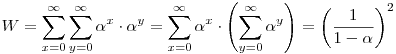
a mértani sor összegzőképlete szerint. A feladatokhoz pedig a P(x) polinomot rendelhetjük, amiről tudjuk, hogy van -1 és +1 között nemnulla gyöke, és tükrözi a zsetonok változását, azaz erre redukálódik a (*) egyenlet egy lépésnyi változás során. A VV-s példában ez a polinom P(x)=2x1-1 volt.
Aki ismer további alkalmazásokat erre a módszerre, örömmel olvasnám azokat.
|
| Előzmény: [3771] Micimackó, 2013-08-07 13:22:20 |
|
|
| [3772] aaaa | 2013-08-07 20:19:50 |
 a) ez ekvivalens n2 darab eredeti feladatbeli (kezdőhelyzet)->(véghelyzet) lehet-e kérdés megválaszolásával.
b) pl. (1;1)-re raksz, erre nem tudod az operációt alkalmazni.
|
| Előzmény: [3770] w, 2013-08-03 14:03:32 |
|





 tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy
tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy 
 szabályos, így BP0C
szabályos, így BP0C =120o és BP0’A’
=120o és BP0’A’

 0
0  x
x
 szám kell nekünk, melyre az
szám kell nekünk, melyre az  (-1;+1) esetén következik be, és ekkor
(-1;+1) esetén következik be, és ekkor