| [3824] Loiscenter | 2014-01-28 15:17:44 |
 Legyen x=y=0 akkor f(0)=0 . legyen x=y igy f(2x)f(0)=4f(x)f(x) -4x.x.f(x) mivel f(0)=0 ezért 4f(x)f(x)-4x.x.f(x)=0 téhats f(x)=0 vagy f(x)=x.x . ellenörizve igaz mind.( bocsi nem tudtam hatványt irni)
|
| Előzmény: [3822] w, 2014-01-27 22:06:36 |
|
|
| [3822] w | 2014-01-27 22:06:36 |
 Egy "vicces" függvényegyenlet.
Keressük meg az összes f:R R függvényt a következő tulajdonsággal: R függvényt a következő tulajdonsággal:
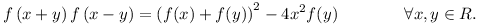
|
|
| [3821] aaaa | 2014-01-26 22:07:48 |
 Ebből még az is következik, hogy:
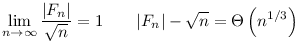
Ugyanis n 64-re 64-re 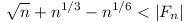 , mert van legalább egy 5-ik hatvány, egyébként finomítva a becslésedet (prímedik hatványokra elég nézni az összeget): , mert van legalább egy 5-ik hatvány, egyébként finomítva a becslésedet (prímedik hatványokra elég nézni az összeget):
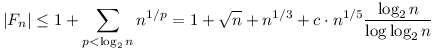
Ugyanis n-ig a prímek száma kb 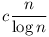 , ebből látszik, hogy elég nagy n-re , ebből látszik, hogy elég nagy n-re
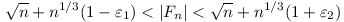
|
| Előzmény: [3817] Ménkűnagy Bundáskutya, 2014-01-26 15:42:40 |
|
|
|
|
| [3817] Ménkűnagy Bundáskutya | 2014-01-26 15:42:40 |
 Azt hiszem, van egyszerűbb is.
Az n-nél kisebb k. hatványok száma legfeljebb n1/k. Itt a k legfeljebb log2n lehet: eltekintve az 1-től a 2 log2n. hatványával még számolni kell, többel biztosan nem. Azaz
|Fn| n1/2+n1/3+...+n1/log2n+1 n1/2+n1/3+...+n1/log2n+1 n1/2log2n+1, n1/2log2n+1,
ami n-nel osztva nyilván 0-hoz tart.
|
| Előzmény: [3815] aaaa, 2014-01-26 01:23:52 |
|
|
| [3815] aaaa | 2014-01-26 01:23:52 |
 Gondolom azt szeretnéd kérdezni, hogy ha Fn={n-nél kisebb hatványszámok}, akkor mi lesz
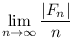
Lemma 1.   , , >0 >0 k0, hogy k>k0 esetén: k0, hogy k>k0 esetén:
![\left|\sum_{i=k}^{[k(1+\varepsilon)] }\frac{1}{i}-\log(1+\varepsilon)\right|<\delta](/kep/keplet.cgi?k=87DEA5C07E25C7AF)
Ez a szokásos integrálós becslésből kijön, legyen ez házi feladat.
Lemma 2. Ha ai pozitív egészek egy növekvő részsorozata, és 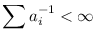 , akkor n-1|An| , akkor n-1|An| 0, ha n 0, ha n  , ha An={ai|ai<n} , ha An={ai|ai<n}
Indirekt, tegyük fel, hogy nem áll fent a bemutatott egyenlőség, vagyis létezik olyan  , hogy |An|> , hogy |An|> n végtelen sokszor. Ha nincs ilyen, akkor pont azt kaptuk, amit akartunk. Legyen n végtelen sokszor. Ha nincs ilyen, akkor pont azt kaptuk, amit akartunk. Legyen 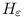 az ilyen n-ek halmaza, ekkor |H|=|N|, vegyük tehát egy olyan bi részsorozatát, ami tudja azt, hogy az ilyen n-ek halmaza, ekkor |H|=|N|, vegyük tehát egy olyan bi részsorozatát, ami tudja azt, hogy  kbi>bi-1, valamely k>2 egészre. Ekkor Abi> kbi>bi-1, valamely k>2 egészre. Ekkor Abi> bi miatt a [0,bi-1] intervallumba maximum bi-1< bi miatt a [0,bi-1] intervallumba maximum bi-1< kbi<Abi kbi<Abi k-1 darab eshet, szóval elég kevés szám, vagyis a számok legalább 1- k-1 darab eshet, szóval elég kevés szám, vagyis a számok legalább 1- k-1-edrésze a jó intervallumba esik. De ekkor az ide eső számok reciprokösszegére alsó becslést ad, ha az intervallumba eső legkisebb számokat vesszük, ebből legalább Abi-Abi-1=bi( k-1-edrésze a jó intervallumba esik. De ekkor az ide eső számok reciprokösszegére alsó becslést ad, ha az intervallumba eső legkisebb számokat vesszük, ebből legalább Abi-Abi-1=bi( - - k-1) darab van: k-1) darab van:
![\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq\sum_{i=[b_i-b_i \varepsilon+\varepsilon^k]}^{b_i}\frac{1}{i}\geq \log\left(1+\frac{\varepsilon-\varepsilon^k}{1-\varepsilon+\varepsilon^k}\right)-\delta](/kep/keplet.cgi?k=18D75B65BBB10C1D)
Az első lemma alapján. De legyen b1 akkora, hogy 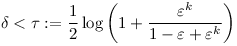 teljesüljön, így azt kaptuk, hogy teljesüljön, így azt kaptuk, hogy ![\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq \tau>0](/kep/keplet.cgi?k=423F09A30C0C85ED) De ekkor De ekkor
![\sum_{a_i<b_k} a_i^{-1}=\sum_{j=1}^{k}\sum_{a_i\in]b_{j-1},b_j]}\frac{1}{a_j}\geq\sum_{j=1}^{k}\tau=k\tau](/kep/keplet.cgi?k=7A2B5BC43AF17040)
Viszont így a reciprokösszeg nem lehet véges.
Lemma 3. A hatványszámok reciprokösszege kisebb, mint 2. Nézzük ugyanis a kövezkező összeget:
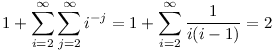
Viszont ab szerepel az a számhoz tartozó részlegösszegben, szóval a hatványszámok reciprokösszege véges.
Lemma 3 miatt teljesül Lemma 2. feltétele, így a hatványszámok felső sűrűsége 0 az egészek körében.
|
| Előzmény: [3814] Loiscenter, 2014-01-24 20:30:06 |
|
| [3814] Loiscenter | 2014-01-24 20:30:06 |
 Hatványszámok valoszinüsége természetes számok körében?
|
|
|
|
| [3811] w | 2013-11-10 16:59:08 |
 201314 mod 73 kiszámítása.
Bár klasszikus feladattípus, szerintem mégis érdekes a megoldás az átlagos feladathoz képest. (Például 999 mod 102 kiszámítása egyszerűbb, hiszen számológéppel is könnyen adódik, hogy 95 -1 (mod 102), ezért elég 99-t mod 10 vizsgálni, ami pedig könnyű.) Most az nem kunszt, ha Euler-Fermat-val lemészároljuk, ámde tökéletesen elfogadható megoldás (ezért tűztem itt ki). Ha egyszerűbb eszközökkel szeretnénk dolgozni, akkor a következő megoldást találhatnánk. -1 (mod 102), ezért elég 99-t mod 10 vizsgálni, ami pedig könnyű.) Most az nem kunszt, ha Euler-Fermat-val lemészároljuk, ámde tökéletesen elfogadható megoldás (ezért tűztem itt ki). Ha egyszerűbb eszközökkel szeretnénk dolgozni, akkor a következő megoldást találhatnánk.
Első célunk keresni olyan n kitevőt, melyre 20n  1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint 1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint

Tehát célszerű n=72 választása, hisz akkor az utolsó tag kivételével minden tag 73-nel osztható, vagyis 2049 -1 (mod 73). -1 (mod 73).
Vagyis csak 1314-t kell mod 49 megnéznünk. De a binomiális tételt újra alkalmazva kapjuk, hogy 1314 1 (mod 49), mert 13 1 (mod 49), mert 13 -1(7). Amiért az adódik, hogy 1314=49 -1(7). Amiért az adódik, hogy 1314=49 +1 alakú, ahol +1 alakú, ahol  tehát páros. Ebből következik, hogy 201314 tehát páros. Ebből következik, hogy 201314 20 (mod 73), vagyis az utolsó három számjegy 026. 20 (mod 73), vagyis az utolsó három számjegy 026.
|
| Előzmény: [3810] csábos, 2013-11-09 16:35:38 |
|
|
|
|
|
| [3806] w | 2013-11-07 16:09:11 |
 Nekem is van egy saját készítésű szép számelméletfeladatom, bár ez évszámok használatának árán könnyebb lesz.
Határozzuk meg a 201314 hatvány 7-es számrendszerbeli alakjában az utolsó három számjegyet.
|
|
| [3805] Sirpi | 2013-10-25 09:19:21 |
 Nekem is ez az eredmény jött ki, bár picit másképp csináltam.
Legyen a k jegyű. Ekkor
(a*)2=(a2)*=a2+11...1
(a*)2-a2=11...1
(a*-a)(a*+a)=11...1
11...1.(a*+a)=11...1
a*+a=11...1/11...1
Ha a k jegyű, akkor a2 vagy 2k-1, vagy 2k jegyű, tehát ennyi db. 1-es van az előző sorok jobb oldalán. Ezt osztjuk le az utolsó sorban egy k db 1-esből álló számmal, és könnyen látható, hogy csak akkor kapunk egész számot, ha 2k db egyesből áll a számláló (sőt, ellenkező esetben a* és a összege kisebb lenne, mint a különbsége).
Ez alapján a*+a=100...01 (k-1 db 0-val), a*-a=11...1, vagyis a=44...45, és ebből csak az 1 és a 2 jegyű megoldás a jó, ahogy azt Te is indokoltad.
|
| Előzmény: [3804] csábos, 2013-10-23 23:21:42 |
|
| [3804] csábos | 2013-10-23 23:21:42 |
 5,45
Tekintsük a feladatot modulo 10k. Legyen
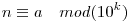
Ekkor a feladat az
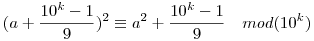
kongruencia formájában írható fel.
Négyzetre emelve, 81-gyel szorozva és a 10k-val osztható tagokat elhagyva a
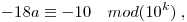
azaz
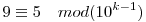
kongruenciához jutunk.
A jobboldalhoz 4.10k-t adva
a=44...445 adódik, azaz az eredeti kongruencia megoldásai
444...445 és 944...445. Ez utóbbi nem játékos, így marad az előbbi.
Ha k legalább 3, akkor 197136=4442<a2<4452=198025. Ezért a2 második jegye 9-es, azaz nem megoldás.
|
| Előzmény: [3803] Sirpi, 2013-10-21 14:26:41 |
|
| [3803] Sirpi | 2013-10-21 14:26:41 |
 A következő egy általam kitalált feladat:
Egy a természetes számra a* jelölje azt a számot, amit úgy kapunk, hogy a minden számjegyét eggyel megnöveljük. Pl: 125*=236. Ha egy számban szerepel 9-es számjegy, akkor nincs értelmezve.
Oldjuk meg az (n*)2=(n2)* egyenletet.
|
|
|
|
|





 R függvényt a következő tulajdonsággal:
R függvényt a következő tulajdonsággal: 
 64-re
64-re  n1/2 igaz minden k
n1/2 igaz minden k
 ,
, >0
>0 k0, hogy k>k0 esetén:
k0, hogy k>k0 esetén:  , ha An={ai|ai<n}
, ha An={ai|ai<n}  -1 (mod 102), ezért elég 99-t mod 10 vizsgálni, ami pedig könnyű.) Most az nem kunszt, ha Euler-Fermat-val lemészároljuk, ámde tökéletesen elfogadható megoldás (ezért tűztem itt ki). Ha egyszerűbb eszközökkel szeretnénk dolgozni, akkor a következő megoldást találhatnánk.
-1 (mod 102), ezért elég 99-t mod 10 vizsgálni, ami pedig könnyű.) Most az nem kunszt, ha Euler-Fermat-val lemészároljuk, ámde tökéletesen elfogadható megoldás (ezért tűztem itt ki). Ha egyszerűbb eszközökkel szeretnénk dolgozni, akkor a következő megoldást találhatnánk.  1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint
1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint  +1 alakú, ahol
+1 alakú, ahol 



