|
| [3835] jonas | 2014-02-19 14:42:13 |
 Szerintem ez a szám a 1016949152542372881355932203389830508474576271186440677966, mert
6.1016949152542372881355932203389830508474576271186440677966=
6101694915254237288135593220338983050847457627118644067796
|
| Előzmény: [3833] Loiscenter, 2014-02-19 11:22:10 |
|
|
| [3833] Loiscenter | 2014-02-19 11:22:10 |
 szürgös:
Egy 6-ra végzödö szám ultolsó jegyét elhagyjuk. Ezt a szám elsö jegye elé irjuk. Az igy kapott szám hatsorosa az eredetinek. Melyik ez a szám? (azaz 6B = B6 . 6 ?)
|
|
| [3832] Sinobi | 2014-02-11 16:29:21 |
 Sinobi: "b, Bizonyítsd be, hogy ha van egy parabolán három pontpár (húr), amelyek felezőmerőlegesei egy ponton mennek át, akkor ha a hat pontot a parabola tengelyirányában elaffinítjuk, akkor az így kapott pontok felezőmerőlegesei is egy ponton fognak átmenni."
Azota sem tudom. Kedvcsinalonak egy hasonlo, de nagyon egyszeru feladat:
Ha van egy parabolan egy ABCD hurnegyszog, azaz barmelyik 2 pont felezomerolegese atmegy egy O ponton, akkor ha a hurnegyszoget a parabola tengelyiranyaban affinitom, akkor az A'B'C'D' pontnegyes is hurnegyszog lesz, azaz barmelyik ket pont felezomerolegese at fog menni O'-n.
Ez ugyan kovetkezik az elozo allitasbol, de azt nem tudom belatni, meg egyszerubben is kijon.
|
| Előzmény: [3795] Sinobi, 2013-10-12 01:30:53 |
|
|
| [3830] Fálesz Mihály | 2014-02-04 20:43:33 |
 Egy kapcsolódó feladat 2007-ből:
A. 429. Határozzuk meg mindazokat az egész együtthatós f(x) és g(x) polinomokat, amikre f(g(x))=x2007+2x+1.
A tanulság valami olyasmi, hogy polinomba polinom  deriválás... :-) deriválás... :-)
|
| Előzmény: [3829] w, 2014-02-03 23:18:11 |
|
| [3829] w | 2014-02-03 23:18:11 |
 550. feladat. (körülbelül)
a) Vannak-e olyan f,g,h másodfokú polinomok, melyekre az 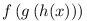 polinom pontosan az 1,2,3,4,5,6,7,8 helyeken nulla? polinom pontosan az 1,2,3,4,5,6,7,8 helyeken nulla?
b) Határozzuk meg azokat az f,g,h polinomokat, melyekre 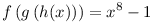 . .
[Ezek nem nehéz, de érdekes feladatok. Ha eddig nem lett volna világos, aki ismeri őket, ne lője le. Aki maga megoldotta a feladatot, annak viszont szívesen látom megoldását.]
|
|
| [3828] Loiscenter | 2014-01-29 00:47:03 |
 1. legyen x=y=0 => f(0) = 0; 2) legyen x=y => 4f(x)[ f(x) - x.x] = 0 => vagy f(x) = 0 vagy f(x)=x.x külön x értékre
3) minden t# 0 esetére ha f(t) = t.t # 0 => legyen x=0, y=t => f(t).f(-t) =f(t)f(t) => f(-t) = f(t)=t.t; ha f(t) = 0 => legyen x=0, y=-t => f(t).f(-t) =f(-t)f(-t) => f(-t) = f(t)=0 összefoglalva f(-x)=f(x) minden x estére.
4) Ha létezik a# 0 ugy , hogy f(a)=0 => akkor minden t# 0 esetére legyen x=t, y=a => f(t+a)f(t-a) = f(t)f(t) legyen x=a, y=t => f(t+a)f(a-t) = f(t)f(t) - 4a.a.f(t) Mivel f(t-a) = f(a-t) => 4a.a.f(t) = 0 => f(t)=0
összegezve : f(x)=0 és f(x) = x.x; a két valosfüggvény , amely teljesiti a feltételt.
(Prof. Hung Son Nguyen - Varso egyetemból)
|
| Előzmény: [3827] Loiscenter, 2014-01-28 20:46:14 |
|
|
|
| [3825] nadorp | 2014-01-28 15:33:25 |
 Ez így egy kicsit hiányos.
Ugyanis abból, hogy minden x-re f2(x)=x2f(x) teljesül, csak az következik, hogy f(x)=0 vagy f(x)=x2, de ez még nem zárja ki azt, hogy pld f(2)=4 és f(5)=0 egyszerre teljesüljön.
|
| Előzmény: [3824] Loiscenter, 2014-01-28 15:17:44 |
|
| [3824] Loiscenter | 2014-01-28 15:17:44 |
 Legyen x=y=0 akkor f(0)=0 . legyen x=y igy f(2x)f(0)=4f(x)f(x) -4x.x.f(x) mivel f(0)=0 ezért 4f(x)f(x)-4x.x.f(x)=0 téhats f(x)=0 vagy f(x)=x.x . ellenörizve igaz mind.( bocsi nem tudtam hatványt irni)
|
| Előzmény: [3822] w, 2014-01-27 22:06:36 |
|
|
| [3822] w | 2014-01-27 22:06:36 |
 Egy "vicces" függvényegyenlet.
Keressük meg az összes f:R R függvényt a következő tulajdonsággal: R függvényt a következő tulajdonsággal:
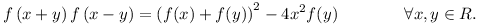
|
|
| [3821] aaaa | 2014-01-26 22:07:48 |
 Ebből még az is következik, hogy:
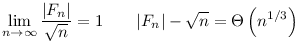
Ugyanis n 64-re 64-re 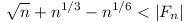 , mert van legalább egy 5-ik hatvány, egyébként finomítva a becslésedet (prímedik hatványokra elég nézni az összeget): , mert van legalább egy 5-ik hatvány, egyébként finomítva a becslésedet (prímedik hatványokra elég nézni az összeget):
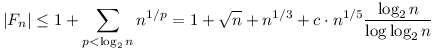
Ugyanis n-ig a prímek száma kb 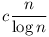 , ebből látszik, hogy elég nagy n-re , ebből látszik, hogy elég nagy n-re
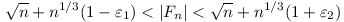
|
| Előzmény: [3817] Ménkűnagy Bundáskutya, 2014-01-26 15:42:40 |
|
|
|
|
| [3817] Ménkűnagy Bundáskutya | 2014-01-26 15:42:40 |
 Azt hiszem, van egyszerűbb is.
Az n-nél kisebb k. hatványok száma legfeljebb n1/k. Itt a k legfeljebb log2n lehet: eltekintve az 1-től a 2 log2n. hatványával még számolni kell, többel biztosan nem. Azaz
|Fn| n1/2+n1/3+...+n1/log2n+1 n1/2+n1/3+...+n1/log2n+1 n1/2log2n+1, n1/2log2n+1,
ami n-nel osztva nyilván 0-hoz tart.
|
| Előzmény: [3815] aaaa, 2014-01-26 01:23:52 |
|
|
| [3815] aaaa | 2014-01-26 01:23:52 |
 Gondolom azt szeretnéd kérdezni, hogy ha Fn={n-nél kisebb hatványszámok}, akkor mi lesz
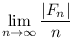
Lemma 1.   , , >0 >0 k0, hogy k>k0 esetén: k0, hogy k>k0 esetén:
![\left|\sum_{i=k}^{[k(1+\varepsilon)] }\frac{1}{i}-\log(1+\varepsilon)\right|<\delta](/kep/keplet.cgi?k=87DEA5C07E25C7AF)
Ez a szokásos integrálós becslésből kijön, legyen ez házi feladat.
Lemma 2. Ha ai pozitív egészek egy növekvő részsorozata, és 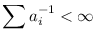 , akkor n-1|An| , akkor n-1|An| 0, ha n 0, ha n  , ha An={ai|ai<n} , ha An={ai|ai<n}
Indirekt, tegyük fel, hogy nem áll fent a bemutatott egyenlőség, vagyis létezik olyan  , hogy |An|> , hogy |An|> n végtelen sokszor. Ha nincs ilyen, akkor pont azt kaptuk, amit akartunk. Legyen n végtelen sokszor. Ha nincs ilyen, akkor pont azt kaptuk, amit akartunk. Legyen 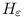 az ilyen n-ek halmaza, ekkor |H|=|N|, vegyük tehát egy olyan bi részsorozatát, ami tudja azt, hogy az ilyen n-ek halmaza, ekkor |H|=|N|, vegyük tehát egy olyan bi részsorozatát, ami tudja azt, hogy  kbi>bi-1, valamely k>2 egészre. Ekkor Abi> kbi>bi-1, valamely k>2 egészre. Ekkor Abi> bi miatt a [0,bi-1] intervallumba maximum bi-1< bi miatt a [0,bi-1] intervallumba maximum bi-1< kbi<Abi kbi<Abi k-1 darab eshet, szóval elég kevés szám, vagyis a számok legalább 1- k-1 darab eshet, szóval elég kevés szám, vagyis a számok legalább 1- k-1-edrésze a jó intervallumba esik. De ekkor az ide eső számok reciprokösszegére alsó becslést ad, ha az intervallumba eső legkisebb számokat vesszük, ebből legalább Abi-Abi-1=bi( k-1-edrésze a jó intervallumba esik. De ekkor az ide eső számok reciprokösszegére alsó becslést ad, ha az intervallumba eső legkisebb számokat vesszük, ebből legalább Abi-Abi-1=bi( - - k-1) darab van: k-1) darab van:
![\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq\sum_{i=[b_i-b_i \varepsilon+\varepsilon^k]}^{b_i}\frac{1}{i}\geq \log\left(1+\frac{\varepsilon-\varepsilon^k}{1-\varepsilon+\varepsilon^k}\right)-\delta](/kep/keplet.cgi?k=18D75B65BBB10C1D)
Az első lemma alapján. De legyen b1 akkora, hogy 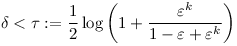 teljesüljön, így azt kaptuk, hogy teljesüljön, így azt kaptuk, hogy ![\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq \tau>0](/kep/keplet.cgi?k=423F09A30C0C85ED) De ekkor De ekkor
![\sum_{a_i<b_k} a_i^{-1}=\sum_{j=1}^{k}\sum_{a_i\in]b_{j-1},b_j]}\frac{1}{a_j}\geq\sum_{j=1}^{k}\tau=k\tau](/kep/keplet.cgi?k=7A2B5BC43AF17040)
Viszont így a reciprokösszeg nem lehet véges.
Lemma 3. A hatványszámok reciprokösszege kisebb, mint 2. Nézzük ugyanis a kövezkező összeget:
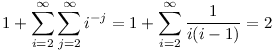
Viszont ab szerepel az a számhoz tartozó részlegösszegben, szóval a hatványszámok reciprokösszege véges.
Lemma 3 miatt teljesül Lemma 2. feltétele, így a hatványszámok felső sűrűsége 0 az egészek körében.
|
| Előzmény: [3814] Loiscenter, 2014-01-24 20:30:06 |
|
| [3814] Loiscenter | 2014-01-24 20:30:06 |
 Hatványszámok valoszinüsége természetes számok körében?
|
|
|
|







 deriválás... :-)
deriválás... :-)  R függvényt, melyre f(x)2=1 teljesül minden x-re.
R függvényt, melyre f(x)2=1 teljesül minden x-re.

 64-re
64-re  n1/2 igaz minden k
n1/2 igaz minden k
 ,
, >0
>0 k0, hogy k>k0 esetén:
k0, hogy k>k0 esetén:  , ha An={ai|ai<n}
, ha An={ai|ai<n}