|
|
| [3884] w | 2014-06-17 11:48:40 |
 Oldjuk meg a következő diofantoszi egyenleteket:
a) &tex;\displaystyle a^4+b^2=c^4&xet;,
b) &tex;\displaystyle a^4+b^4=c^2&xet;.
|
|
|
| [3882] pelike | 2014-04-20 11:25:09 |
 Egy egyszerű, de "mindennapi élethez köthető" feladat:)
A "Kérem a következőt!" című vetélkedőben egy kör 4 kérdést tartalmaz, minden kérdésre 2 válaszlehetőséggel. Egy kör sikeres, amennyiben legalább 3 jó válasz érkezik.
Tegyük fel, hogy Játékosunk pontosan 2 kérdésre tudja a választ és azokra a kérdésekre, amelyekre nem tudja a választ, semmilyen háttér információja sincs, tehát vakon tippel.
Mekkora eséllyel veszi sikerrel a kört Játékosunk?
|
|
|
|
| [3879] juantheron | 2014-04-15 05:51:39 |
 If &tex;\displaystyle f:R\rightarrow R&xet; and &tex;\displaystyle f(f(x)) = 3x&xet;, Then &tex;\displaystyle f(2013)&xet;
|
|
| [3878] w | 2014-03-31 19:03:17 |
 Egy szép kis saját feladat:
Van-e olyan injektív &tex;\displaystyle f(x)&xet; valós függvény, amihez vannak olyan &tex;\displaystyle a,b>0&xet; konstansok, melyek esetén bármely valós &tex;\displaystyle x&xet;-re
&tex;\displaystyle f\big(x^2\big)-\left(f(ax+b)\right)^2\ge \frac14&xet;
teljesül?
|
|
|
|
| [3875] Micimackó | 2014-03-25 23:26:34 |
 Adott n-re, mennyi az n elemű halmaz fixpont mentes permutációinak paritása?
|
|
|
| [3873] jonas | 2014-03-13 21:13:23 |
 Helyes, a véges várható érték. Akkor most jön a megoldás trükkösebb része.
Rögztsük a játékos egy stratégiáját. Jelölje Fn a játék állapotát n lépés után. Ez tartalmazza a játékos által kiválasztott két golyót és a játékvezető érmedobását az első n lépésben.
Legyen Xn az a szám, ahányféleképpen a játékos megválaszthatná a két különböző golyót az (n+1)-edik lépésében. Azért számozom így, mert Xn az Fn függvénye. Nyilván X0=n(n-1), mivel a kezdőhelyzetben bármely két golyó különböző. Feltéve, hogy a játék n lépés után még nem ért véget, számoljuk ki az E(Xn+1-Xn|Fn) feltételes várható értéket!
Ha ez megvan, akkor alkalmazzuk a martingál megállási tételt egy megfelelő martingálra, és ezzel oldjuk meg az (a) és (b) feladatot.
|
| Előzmény: [3872] Róbert Gida, 2014-03-13 17:22:28 |
|
| [3872] Róbert Gida | 2014-03-13 17:22:28 |
 Nem jött megoldás, így lelövöm. Kezdetben n szín van, a játék véget ér, ha egy szín marad. Tetszőleges n2 egymásutáni fordulóban (1 forduló amikor 2 golyót a játékvezetőnek adunk és 2-t visszakapunk) van olyan szín ami legalább n-szer szerepel az odaadott golyószínek között (skatulyaelv, sőt van ami legalább 2n-szer), és legfeljebb persze n2-szer (mindez stratégiától függetlenül igaz). Ha ezen fordulók mindegyikében pont a másik színből adott vissza a játékvezető, akkor ebből a színből több nem marad (és később sem jöhet "vissza" a szabályok miatt). Ennek valószínűsége legalább 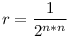 . Nézzünk n-1 egymásutáni blokkot, azaz n2 hosszú fordulót, ha minden blokkban vesztünk egy színt, akkor a játék természetesen véget ér, ennek a valószínűsége legalább q=rn-1. Azaz annak a valószínűsége, hogy n2(n-1) fordulóban befejeződik a játék legalább q, így annak a valószínűsége, hogy nem fejeződik be a játék legfeljebb s=1-q<1. . Nézzünk n-1 egymásutáni blokkot, azaz n2 hosszú fordulót, ha minden blokkban vesztünk egy színt, akkor a játék természetesen véget ér, ennek a valószínűsége legalább q=rn-1. Azaz annak a valószínűsége, hogy n2(n-1) fordulóban befejeződik a játék legalább q, így annak a valószínűsége, hogy nem fejeződik be a játék legfeljebb s=1-q<1.
Ebből már készen vagyunk, mert ekkor Pr2(m)=Pr(játék m lépésben nem fejeződik be)<c*pm, ahol c>0,p<1 (Miért is? Bontsuk fel az m fordulót n2(n-1) hosszú fordulókra, bármelyiket is választjuk legfeljebb s<1 valószínűséggel nem ér benne véget a játék, így m forduló után is játszunk legfeljebb 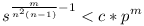 valószínűséggel .) valószínűséggel .)
Legyen Pr1(m)=Pr(játék pontosan m lépésben ér véget), ekkor 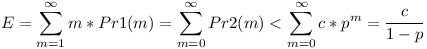 , azaz véges a várható érték, stratégiától függetlenül. , azaz véges a várható érték, stratégiától függetlenül.
Sőt itt valamivel többet is beláttam, hiszen c,p csak n-től függött (de a stratégiától nem), azaz létezik v(n) véges szám, hogy a várható érték kisebb, mint v(n). Itt v(n) egyébként ki is számolható.
|
| Előzmény: [3871] jonas, 2014-03-12 10:10:43 |
|
|
| [3870] jonas | 2014-03-11 21:03:52 |
 Ezt a feladatot nem volt jó ötlet ezen a fórumon feladnom, mert a megoldásához túl sok előismeret kell. A középiskolás fórumozóktól ezért elnézést kérek.
|
| Előzmény: [3861] jonas, 2014-03-09 16:36:46 |
|
| [3869] jonas | 2014-03-11 17:42:59 |
 Aha, értem! Bocsánat, hogy nem fogalmaztam egyértelműen. Valóban, a játékvezető nem adja vissza a két golyót, amit odaadtál neki, így minden lépés után pontosan n golyó lesz nálad.
|
| Előzmény: [3868] Róbert Gida, 2014-03-11 17:28:14 |
|
| [3868] Róbert Gida | 2014-03-11 17:28:14 |
 Jó a megoldásom, csak egy másik feladatra. Az persze számomra nem volt világos, hogy a játékvezető a két golyót lenyúlja amit odaadsz neki, így persze nálad mindig n golyó lesz, az én feladatomban pedig minden lépés után 2-vel több.
|
| Előzmény: [3867] jonas, 2014-03-11 11:46:28 |
|
| [3867] jonas | 2014-03-11 11:46:28 |
 A számok, amiket megadtál, szerintem nem stimmelnek. n=3 esetén az első lépés után három golyóból két egyforma színű, és egy különböző lesz. Ez után minden további lépés után 1/2 valószínűséggel nyertél, 1/2 valószínűséggel visszajutsz egy hasonló állapothoz, csak most a másik színből van két golyód, mint az előbb. Így aztán biztosan legalább 2 lépés kell a nyerésig, nem 1, mint a táblázatban mutatod. Nem nehéz belátni, hogy a lépések várható száma pontosan 3.
Látható, hogy n=3 esetén még lényegében nincs választásod a játék során. A következő, n=4 esetben már van választásod. Például ha az első lépés után két fehér, egy sárga, és egy piros golyód van, akkor kétféleképpen dönthetsz. Odaadhatod a játékvezetőnek a sárga és a piros golyót, ez a kevésbé kockázatos stratégia, mert ekkor legközelebb biztosan két fehér és két másik azonos színű golyód van. Vagy kockáztathatsz, odaadva a játékvezetőnek egy fehér és egy sárga golyót, ekkor 1/2 valószínűséggel már három fehér golyód lesz, amivel közelebb jutottál a nyeréshez; de 1/2 valószínűséggel két sárga, egy fehér és egy piros golyód lesz, amivel helyben maradtál.
Te választod meg a stratégiát, de a feladat kitűzésében azt állítottam, hogy a lépések számának várható értéke bármely stratégia esetén ugyanannyi.
|
| Előzmény: [3864] Róbert Gida, 2014-03-10 21:20:33 |
|
|
| [3865] Róbert Gida | 2014-03-10 21:39:02 |
 Optimális stratégiával a sorozat első 20 tagja (Neil adatbázisában nincs benne a számlálók sorozata, a nevezők 2 hatványok)
1 0
2 1
3 1
4 5/2
5 5/2
6 33/8
7 33/8
8 93/16
9 93/16
10 965/128
11 965/128
12 2379/256
13 2379/256
14 11333/1024
15 11333/1024
16 26333/2048
17 26333/2048
18 480429/32768
19 480429/32768
20 1079775/65536
|
| Előzmény: [3864] Róbert Gida, 2014-03-10 21:20:33 |
|
| [3864] Róbert Gida | 2014-03-10 21:20:33 |
 "Minden lépésben megnézed a golyókat"
"A várható érték miért ugyanannyi függetlenül attól, hogy melyik golyókat választod?"
Játszhatok egy stratégia szerint, vagy véletlenül kell a golyókat kiválasztanom? Optimális stratégiával O(n) lesz a válasz: mindig a két eddig legtöbbet kihúzott színt választom (ha több lehetőség van, akkor véletlenül döntök a leggyakoribbak közül), ez persze mese eddig, hogy miért is ez lenne az opt. Várható értéket sem mutatja, de sokkal könnyebben kiszámítható ezzel a várható érték.
Míg hülyén játszva O(n2). Teljesen véletlenül játszva is érdekes (lehet) a feladat.
|
| Előzmény: [3861] jonas, 2014-03-09 16:36:46 |
|
| [3863] jonas | 2014-03-10 07:35:16 |
 Igen, veheted úgy, hogy a játékvezető csukott szemmel választ egyet. Én úgy képzelem, hogy egy golyót a játékvezető jobb kezébe adsz, egyet a bal kezébe. Ezután ha a játékvezető fejet dob, akkor két olyat ad vissza, amilyen a bal kezében van, ha írást, akkor két olyat, ami a job kezében van.
|
| Előzmény: [3862] BohnerGéza, 2014-03-10 03:13:18 |
|
| [3862] BohnerGéza | 2014-03-10 03:13:18 |
 Nem értem biztosan a feladatot. Ki dönti el, melyik az egyik illetve másik? Azt akarja jelenteni, amit így kapunk?
... A két kiválasztott közül csukott szemmel választ egyet és két ilyen színű kerül vissza. ...
n=1 esetén 0, n=2 esetén 1 a várható érték. A többi néhány esetet ehhez jobban értőkre bízom!
|
| Előzmény: [3861] jonas, 2014-03-09 16:36:46 |
|









