| [393] Fálesz Mihály | 2004-06-18 14:06:40 |
 Mutassunk példát olyan valós függvényre, ami csak a 0-ban differenciálható, de ott kétszer is.
|
|
|
| [391] Sirpi | 2004-06-17 16:38:57 |
 Komplex számok ismerete nélküli megoldásként én arra gondoltam...
Igen, ez az egyszerű, de a második hozzászólásomban erre már én is rájöttem :-)
Az alapállítást f(1)=-1 jelenti, csak (*)-ból nem jöhet ki az állítás.
Teljesen jogos, pontatlanul fogalmaztam. A megoldás vázlata kb. így néz ki:
f(k+3)=f(k)f(3)-f(k-3)=2f(k)-f(k)=f(k), kihasználva az indukciót, a (*) összefüggést, valamint azt, hogy f(3)=2. Utóbbi pedig könnyen látszik, még ha nem is közvetlenül számolunk, akkor is: f(2)=f(1)f(1)-f(0)=1-2=-1, f(3)=f(1)f(2)-f(1)=(-1)2-(-1)=2
Tudom, túlragoztam a dolgot...
|
| Előzmény: [390] lorantfy, 2004-06-17 16:01:24 |
|
| [390] lorantfy | 2004-06-17 16:01:24 |
 Szia Sirpi!
Tetszik az f(k) függvényed! Az alapállítást f(1)=-1 jelenti, csak (*)-ból nem jöhet ki az állítás.
Komplex számok ismerete nélküli megoldásként én arra gondoltam, hogy mivel a=1 nem megoldása az egyenletnek, be lehet szorozni mindkét oldalt (a-1)-el.
Így (a-1)(a2+a+1)=0 vagyis a3-1=0 és ha a3=1 akkor persze a2004=1, tehát a keresett kifejezés értéke 2.
Persze a megoldás elég "misztikus" annak aki a komplex számokat nem ismeri. Hogy lehet az, hogy a 1 és a3=1? 1 és a3=1?
|
| Előzmény: [388] Sirpi, 2004-06-17 13:01:13 |
|
| [389] Sirpi | 2004-06-17 15:08:06 |
 Lehet, hogy elbonyolítottam...
0=0(a-1)=(a2+a+1)(a-1)=a3-1, ahonnan a3=1. Innen pedig a2004=(a3)668=1, ennek a reciproka is 1, összegük 2, ez tehát a végeredmény. Hogy minek gépeltem az előbb ennyit???
|
| Előzmény: [388] Sirpi, 2004-06-17 13:01:13 |
|
| [388] Sirpi | 2004-06-17 13:01:13 |
 Ez a 84. feladat poénos. A valós számok korében ugyanis nem teljesül a kezdeti feltétel, hiszen 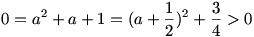 , de ettől pl. a komplex számok körében meg lehet a feladatot oldani. , de ettől pl. a komplex számok körében meg lehet a feladatot oldani.
Viszont az is meg tudja oldani a feladatot, aki nem is hallott a komplex számokról.
Vezessük be a következő jelölést: f(k)=ak+a-k.
Ekkor f(k)f(l)=(ak+a-k)(al+a-l)=(ak+l+a-(k+l))+(ak-l+a-(k-l))=f(k+l)+f(k-l)
Vagyis: f(k+l)=f(k)f(l)-f(k-l) (*)
Mi éppen f(2004)-et akarjuk kiszámolni. Amit tudunk a fenti összefüggésen kívül, az az, hogy f(0)=2, f(1)=-1 és f(k)=f(-k) minden egész k-ra.
Állítás: f(k+3)=f(k) minden k-ra, ez indukcióval bizonyítható a (*) összefüggésből (ezt a részt, ami nem is túl nehéz, rábízom másra). Innen f(2004)=f(0)=2.
/persze tudom, hogy a egy harmadik egységgyök, és innen triviálisan kijön a 2, mint megoldás, de elemi módszerekkel próbáltam a feladatot megoldani./
|
| Előzmény: [387] lorantfy, 2004-06-17 11:35:20 |
|
| [387] lorantfy | 2004-06-17 11:35:20 |
 84. feladat: Ha a2+a+1=0, akkor mennyi az értéke a
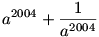
kifejezésnek?
|
|
| [386] Hajba Károly | 2004-05-30 19:52:40 |
 Kedves László!
Gratula, a feladat megoldva. Ti. a séta mindennapos esemény, így már másnap kimegy az első és kezdődhet a kapcsolgatás, továbbá a kapcsoló tényleg kezdetben lekapcsolt állapotban van, így ez nem probléma.
Ezzel kapcsolatban eszembe jutott egy bónusz kérdés.
Határozzuk meg annak valószínűségét, hogy pontosan 1, 2, .. stb. év múlva milyen valószínűséggel lesznek még benn a rabok. (Szökőnapokat praktikusan nem vegyük számításba.)
HK
|
| Előzmény: [385] lorantfy, 2004-05-30 19:04:39 |
|
| [385] lorantfy | 2004-05-30 19:04:39 |
 Kedves Károly!
Kösz a biztatást!
Megörültem, hogy Gyuri a feladatba beleírta, hogy tfh. a kapcsoló le van kapcsolva, de nyilván foglalkozni kell azzal az esettel is ha először felkapcsolt helyzetben van.
Azt hiszem erre az lenne a legjobb megoldás, hogy a megbeszélésen ne jelöljenek ki egy fix számoló embert, hanem kimondják, legyen az a számoló akit a megbeszélés utáni első nap visznek ki sétálni. Mikor kimegy lekapcsolt helyzetbe állítja a kapcsolót és kezdődhetnek a számolási körök.
Ha a kapcsoló alaphelyzete nem ismert és előre kijelölik a számláló embert, akkor az a probléma, hogy amikor először kijut a számláló és azt látja, hogy a kapcsoló fel van kapcsolva, nem tudja, hogy ez volt a kapcsoló alaphelyzete, vagy az első ember kapcsolta fel. Így a számolás 1-el csúszhat.
Erre az a megoldás, hogy megbeszélik előre, hogy akit a megbeszélés utáni első nap visznek ki, az mindenképpen fel állásba állítja a kapcsolót akárhogy is állt és többször nem kapcsol ha máskor kiviszik sétálni.
Még egy probléma lehet, ha a rabok nem tudják előre, hogy a megbeszélés után hányadik naptól kezdve visznek ki minden nap egy embert sétálni.
Ekkor, akit pl a 2. napon visznek ki sétálni, azt gondolhatja, lehet, hogy ő az első. Ezen még gondolkodom.
|
| Előzmény: [384] Hajba Károly, 2004-05-30 17:11:08 |
|
| [384] Hajba Károly | 2004-05-30 17:11:08 |
 Kedves László!
A feladat lényegét már megoldottad, csak a kezdeti ún. "peremfeltételeket" kellene még tisztázni. Ki lesz a kijelölt ember, milyen állapotban van kezdetben a kapcsoló és ezt ki kapcsolta oda. Mi történik addig, míg először kiengedik a kijelölt embert?
Üdv: HK
|
| Előzmény: [383] lorantfy, 2004-05-30 13:55:14 |
|
| [383] lorantfy | 2004-05-30 13:55:14 |
 82.feladathoz: Mivel csak egy kétállású kapcsolónk van, ezzel csak 1 embert lehet "megszámolni" azután vissza kell állítani alaphelyzetbe. Tehát ki kell jelölni egy nullázó-számlázó embert a rabok közül. Ezenkívül megegyeznek, hogy minden ember csak egyszer kapcsolhatja fel a kapcsolót, de csak akkor ha a sétája során lekapcsolva találja.
Így a számláló ember két sétája között, ha kiengednek egy új embert is, akkor az felkapcsolja a kapcsolót. A számláló ember a következő sétáján megnézi a kapcsolót, ha felkapcsolva találja, akkor növeli eggyel a már kiengedett rabok számát és lekapcsolja a kapcsolót, ha lekapcsolva találja, akkor nem járt kint közben új ember.
Tudja, hogy a rabok száma n, így n-1-nél már szólhat, hogy mindenki járt kint.
Hát, elég sokáig eltarthat a dolog, de mivel minden rab csak egyszer kapcsolhatja fel a kapcsolót, a számláló előbb-utóbb eljut n-1-ig és akkor kiszabadulnak.
|
| Előzmény: [361] Gyuri, 2004-05-24 14:08:19 |
|
| [382] Hajba Károly | 2004-05-30 13:42:42 |
 83. feladat:
Vizsgáljuk meg a következő állítások igazságtartalmát:
a) Ez a mondat igaz.
b) Ez a mondat hamis.
Nos? :o)
HK
|
|
| [381] Hajba Károly | 2004-05-28 10:59:37 |
 Kedves Csimby!
Ne is mond el a választ, gondolkodom rajta, s a gondolataimat leírom. Az eddigi termés:
Egy N+ szám nem lehet négyzetszám, ha (N mod 5)=(2, 3). Azaz, ha egy szám 5-tel történő osztásának maradéka 2 vagy 3, nem lehet négyzetszám. (Remélem jól írtam fel a képletet.) Gyakorlatilag, ha 2, 3, 7, 8-ra nem végződhet négyzetszám.
Ez az utolsó számjegy vizsgálata, de tovább lehet finomítani, ha nem egy, hanem 2 vagy több utolsó számjegyet vizsgálunk. Például, ha az utolsó 2 jegyet vesszük, akkor a 100 lehetőségből 22 lehet négyzetszám, ciklikusan, huszas eltolással, de ezek vége sem lehet a fenti négy szám.
Másik oldalról a sorozat utolsó jegyeire is kellene találni valami törvényszerűséget, melyet összevethetünk az előbbiekkel. Hát itt még nem sok mindent találtam. Paritása: -, -, +, -, -, +, ... A számok rendjére még nincs semmi ötletem. Minden csűrés-csavarás után visszakapom az eredeti sor jellegét.
Ha van valami ötleted, szólj.
Üdv: HK
|
| Előzmény: [367] Csimby, 2004-05-25 22:53:41 |
|
| [380] Hajba Károly | 2004-05-26 15:10:53 |
 Kedves Gyuri!
81. feladathoz
Van egy ötletem az 5 lépéses megoldásra, de sem időm, sem türelmem nincs jelenleg a kidolgozásra. Tehát:
Az 1. lépésben vagy átlósan vagy szomszédosan megvizsgálom a kapcsolók állapotát, de nem változtatok rajta. A 2. lépésben a másik módon vizsgálom meg, így két kapcsolóról konkrét adatom van, de egy harmadikról is lehet elég sok infóm, sőt bizonyos esetekben még a 4.-ről is. Ezek ismeretében a 2. lépésben úgy kapcsolok, hogy Syllabus 7 lépéses módszerének középállapotához jussak. Innen 1-2-1 és kész. Természetesen minden állapot megvizsgálása nélkül nem tudom, hogy mindenképpen el tudok-e ide jutni a 2. lépés során.
Üdv
PS. A hálón szokásos illemszabály szerint teljes nyugalommal tegeződhetünk. :o)
|
| Előzmény: [378] Gyuri, 2004-05-26 14:14:36 |
|
| [379] syllabus | 2004-05-26 15:06:19 |
 Valóban a megoldás során nem vizsgáljuk, hogy milyen állapotban fogjuk meg a kapcsolókat.
Bármilyen állapotban is vannak, ezután a 7 kapcsolás után biztosan kinyílnak.
Esetszétválasztással valóban 5 lépésben kinyitható az "ördöngős lakat". :)
|
| Előzmény: [377] Gyuri, 2004-05-26 13:40:35 |
|
| [378] Gyuri | 2004-05-26 14:14:36 |
 Kedves Syllabus!
Megértettem a megoldásukat, hibátlan. 1-2-1 vagy kinyitja a zárat, vagy 3. vagy 4. állapotba viszi. 3 pedig 1. vagy 2. állapotba visz. Ezután 1-2-1 újra, s nyitva a zár.
Mindenesetre várom az 5 lépéses megoldást is :)
Szintén a 81-es feladathoz lenne hozzáfüznivalóm. Legyen L db lyuk a kapcsolón, és K db kezünk! A megoldást sajnos nem tudom. Annyit csak, hogy prím L esetén K-nak legalább L-1 -nek kell lennie, hogy biztosan nyitható legyen a zár. Továbbá páros L esetén K=L-2 is elég. Ha mondjuk s()-sel jelölöm a minimálisan szükséges kezek számát a lyukak számának függvényében, akkor: s(3)=2, s(4)=2, s(5)=4, s(6)=4, s(7)=6 de pl. s(8)=?
|
|
|
|
|
| [374] Gyuri | 2004-05-26 12:40:20 |
 Kedves Syllabus!
81-eshez: Érezzük azt is, hogy melyik kapcsoló melyik állásban van. Mondjuk kitapinthatjuk, hogy 0 vagy 1 az állapota. És véges algoritmus kell!
|
| Előzmény: [365] syllabus, 2004-05-25 21:36:12 |
|
|
| [372] Hajba Károly | 2004-05-26 03:52:50 |
 Kedves Syllabus!
A 2. lépés után be kell iktatni újból egy 1-es eljárást és akkor jó lesz. Lehet, hogy csak elfelejtetted beírni. :o)
Tehát az eljárások sorrendje a következő: 1-2-1-3-1-2-1.
Továbbá a 3-as és 4-es állapotot nem kell megkülönböztetni, mivel izomorfak az eljárás szempontjából.
HK
|
| Előzmény: [369] syllabus, 2004-05-26 00:02:54 |
|
| [371] Hajba Károly | 2004-05-26 03:18:20 |
 Kedves Syllabus!
Ha jól követtem a gondolatmenetedet akkor a kezdetben 2-es állapotnak lehetséges még zárt állapota:
1. lépés: 1. eljárás - 2-es állapot
2. lépés: 2. eljárás - kinyit v. 1. állapot
3. lépés: 3. eljárás - 3. v. 4. állpot
4. lépés: 1. eljárás - 4. v. 3. állapot
5. lépés: 2. eljárás - 3. v. 4. állapot
:o(
HK
|
| Előzmény: [369] syllabus, 2004-05-26 00:02:54 |
|
|
| [369] syllabus | 2004-05-26 00:02:54 |
 81:
Négy eset lehetséges:
1. 2. 3. 4. 10 11 11 00 01 00 01 10
1. eljárás: Két szembenlévőt megfogom és mindkettőt megcserélem. 2. eljárás: Két egymásmellett lévőt megfogom és mindkettőt megcserélem. 3. eljárás: Két egymásmellett lévőt megfogom és az egyiket megcserélem.
1. lépés: Alkalmazom az 1. eljárást.
Az 1. esetben kinyílt, a 2. eset marad, a 3. és 4. egymásba átvált.
2. lépés: 2. eljárás.
A 2. esetben kinyílt, a 3. és 4. egymásba átvált vagy marad.
(Már csak 3-1-es lehet a kapcsolók állása. :)
3. lépés: 3. eljárás.
Vagy kinyílt, vagy 1-es vagy 2-es esetbe került a zár.
4. lépés: 1. eljárás.
Ha 1-esben volt, akkor kinyílt, ha 2-esben akkor maradt 2-eske.
5. lépés: 2. eljárás.
Heuréka! :)))
|
|





 1 és a3=1?
1 és a3=1? 


