| [418] lorytibi | 2004-07-17 20:01:28 |
 Na, ez a jól elgondolkodtató feladat után feladok egy másikat, amit ugyancsak az egyik tanárom edott fel a zalai matektáborban:
89.feladat: Egy asztal előt ülsz bekötött szemmel, az asztalon korongok vannak, amelyeknek egyik oldala kék, a másik meg piros. 100 darab korongnak a piros oldala van fölül, a többinek a kék. Oszd két csoportba a korongokat úgy, hogy a csoportokban ugyanannyi piros(piros része látszik) korong legyen!
- Kitapogathatod, hogy hány korong van, így megtudhatod hány kék.
- Meglehet fordítani őket, (de szerintem azt úgy lenne érdemes, ha az összeset egyszerre megfordítjuk,) hisz, ha csak egyet fordítasz, nem tudhatjuk milyen színű.
Sajnos ennek a feladatnak nem tudom a megoldását, elégé megoldhatatlannak tűnik. Várom a próbálkozásokat!
|
|
| [417] Hajba Károly | 2004-07-16 14:04:56 |
 Kedves Tibi!
Szép kis feladatot hoztál! A 60 aranyas megoldás valóban csak első gondolat volt, később elfogadtam Sirpi gondolatmenetét, engem csak az összeesküvés lehetősége "zavart". Tény, hogy egy ált. isk. feladatba még nem illik behozni a fogoly-dilemmát.
Hát ha 203-nál több kalóz lenne, én azt javasolnám, menjünk még egy kicsit rabolni, hogy legyen mit szétosztani. :o)
Ebben az esetben, ha visszafelé számozzuk a kalózokat azaz a sorszámuk egyben a gonoszságuk mértékének jelzője is, akkor a 203. és következőknek érdeke elfogadni a leosztást, mivel előbb-utóbb ők lesznek az osztók és őket is vízbe dobnák. Így annak ellenére elfogadják a leosztást, hogy ők semmit sem kapnak, sőt még gonoszabbak is az aranyat kapóknál. Azaz a leosztás elfogadásával az életüket védik. (Mivel a cápák már a fekete zászlós hajó körül gyülekeznek. :o)
Üdv: HK
|
| Előzmény: [416] lorytibi, 2004-07-15 17:36:28 |
|
| [416] lorytibi | 2004-07-15 17:36:28 |
 Igen Onogur, elsőnek ténleg elfogadható megoldásnak tűnik, hogy 60-at tartsunk meg magunknak, és 4 kalóznak adjunk 10-et, de ezek után nagyon megdöbbentő, hogy az a 4 kalóz még akkor is rád szavaz, ha 1 aranyat osztasz nekik.
Érdekes lehet a felosztás alakulása, ha a kalózok számát növeljük, de még mindig 100 aranyat kell szétosztanunk. Ha már 201 kalózig eljutunk, sajnos nekünk már nem jut arany, 202 kalóznál még ugyaz az a helyzet, de 203-nál már biztosan vízbe dobnak. Érdemes még tovább növelni a kalózok számát, mert akkor mégérdekesebbé válik a feladat, hisz 203 kalóz után azt hinnénk, hogy mindenféleképpen meghalnánk, de ez nem így van!!!
|
| Előzmény: [410] Hajba Károly, 2004-07-14 15:46:41 |
|
| [415] lorytibi | 2004-07-15 17:23:10 |
 Köszönöm a megoldásokat!
A feladat eredeti szövegében szerepelt még egy feltétel:
A kalózok vérszomjánál csak kapzsiságuk nagyobb.
Ez a feltétel zárja ki azt, hogy a kalózok összebeszéljenek. Bocs,de ezt elfelejtetem beleírni. Sirpi megoldása a helyes.
|
| Előzmény: [414] Hajba Károly, 2004-07-15 16:32:13 |
|
| [414] Hajba Károly | 2004-07-15 16:32:13 |
 Kedves Sirpi!
A gondolatmeneted szerint jó a megoldásod. Ill. válaszolhattad volna az én gonoszkodásomra, hogy ha az utolsó kettőnél az utolsó előtti miért adná oda a felét, ha akkor már az egészet szabályosan is meg tudja szerezni. Ezért nem biztos, hogy együtt tudnak működni.
Csak hát volt egy olyan érzésem, mintha ez az ún. fogoly-dilemmára emlékeztetne.
Üdv: HK
|
| Előzmény: [413] Sirpi, 2004-07-15 13:56:48 |
|
| [413] Sirpi | 2004-07-15 13:56:48 |
 Utóbbi kérdésedre válaszolnék először: az, hogy ki mennyire gonosz, valóban semmit nem számít a feladat szempontjából, maximum annyit, hogy a sorrend a szavazás legelejétől kezdve kötött.
Amúgy pedig az itt megfogalmazott feladatra szerintem teljesen jó a megoldásom. Az összebeszéléseket pedig nem nagyon lehet kezelni, főleg, ha én elsőként jövök, és fogalmam sincs arról se, hogy ki kivel fogott össze. A feladat ezen variációja szerintem nehezen kezelhető, és semmi szép, egyszerű válasz nem adható rá. A Te verziódban, ahol az utolsó 2 összefog, mindenképp ellened fog szavazni addig, amiíg nekik nem adod az összes lóvét, ami teljesen más irányba viszi el a feladatot.
Különben pedig én is megvárnám a feladat feladójának reakcióját az egyébként teljesen jó megoldásomra :-)
Sirpi
|
| Előzmény: [412] Hajba Károly, 2004-07-15 13:17:54 |
|
| [412] Hajba Károly | 2004-07-15 13:17:54 |
 Kedves Sirpi!
A feladat pontos megoldását nem ismerem, most inkább hangosan (betűsen) gondolkodom és kukacoskodom.
Először is remélem, tudsz úszni, hogy ennyire kegyetlen kalóz lennél? :o)
Mint írtad, működik a rendszered, ha nem beszélnek össze ellene, s csak az egyéni érdekeiket nézik. De hát mi az egyéni érdeke bárkinek is? Ha valamely módon kaphatna esetleg többet is, az nem érdeke? Ekkor nem eleve egyedi érdeke-e az összeesküvés? Persze ehhez csoportmunkára és egymás iránti bizalomra is van szükség. Itt mindha egy kis paradoxon kezdene körvonalazódni. (Mi az igazság Tibi? Van biztos megoldás vagy attól függ, hogy mit tekintek érdeknek?)
Ha ebben a rendszerben minden aktuális leggonoszabb kalóz így gondolkodik, s a két utolsó mindig ellene szavaz, így mindig leszavazzák a leosztást. Előbb utóbb rájuk kerül a sor, s ekkor elfelezik a szajrét. Ezt hogy lehet kivédeni ebben a rendszerben?
Hogyan ossza le úgy a főgonosz kalóz, hogy semmi szín alatt ne akarjanak összeesküdni ellene, ne érje meg senkinek? Szerintem így találnánk meg a helyes megoldás.
Eleve mit takar a leggonoszabb kalóz mibenléte? Szerintem a feladat szemontjából akár ABC szerint is következhetnének, csak így jobban hangzik a feladat. Vagy rosszul látom?
Üdv: HK
|
| Előzmény: [411] Sirpi, 2004-07-14 21:35:09 |
|
| [411] Sirpi | 2004-07-14 21:35:09 |
 Még szerencse, hogy nem az a kérdés, Te mit tennél, hanem hogy a kalózok hogyan cselekednének :-). Nekik pedig, racionálisan gondolkodva, el kell fogadniuk az egy aranyat, ugyanis ellenkező esetben a következő kalóz SEMMIT nem adna nekik, tehát még rosszabbul járnának. Feltéve persze, hogy a kalózok nem játszanak össze, mindegyik csak a saját egyéni érdekeit nézi.
Tehát továbbra is fenntartom, hogy ha én kezdenék, 96 0 1 0 1 0 1 0 1 0-val indítanék.
Sirpi
|
| Előzmény: [410] Hajba Károly, 2004-07-14 15:46:41 |
|
| [410] Hajba Károly | 2004-07-14 15:46:41 |
 Kedves Sirpi!
Ha én lennék az 1 aranyas kalóz, bizony az osztó ellen szavaznék ... és zsupsz már a vízben is van.
Szerintem 4 kalóznak meg kell adnia az átlag 10-10 aranyat, hogy mindenképpen mellette szavazzanak, s ekkor már a többi 60 az övé lehet.
HK
|
| Előzmény: [409] Sirpi, 2004-07-14 11:22:59 |
|
| [409] Sirpi | 2004-07-14 11:22:59 |
 Mivel sokáig nem írt megoldást senki, leírom, mire jutottam.
Nézzük meg először, mi a helyzet 2 kalózra. Nyilván aki oszt, az mind a 100-at magának adja, és a másik hiába szavaz ellene, nem tehet semmit.
Három kalóz esetén ezért, ha az osztó a legutolsónak 1 aranyat ad, akkor már maga mellé állítja, mert ha az utolsó a vízbedobásra szavaz, nem kap semmit. Ilyenkor tehát 99 0 1 jó osztás.
4 kalóz esetén 99 0 1 0 megint megteszi (a 3. kalóz ekkor az első mellett fog szavazni, mert különben 0-t kapna, ezzel megvan az 50%).
Stb... 10 kalóz esetén 96 0 1 0 1 0 1 0 1 0 megfelelő leosztás (az egyeseknek érdemes megszavazni a dolgot, különben 0-t kapnának, azaz megvan az 5 szavazat).
Sirpi
Bár, amikor az első kalóz megteszi az ajánlatát, azért nem árt, ha picit aggódik, hogy nem fogtak-e össze néhányan ellene :-)
|
| Előzmény: [408] lorytibi, 2004-07-12 13:15:00 |
|
| [408] lorytibi | 2004-07-12 13:15:00 |
 Matek táborban az egyik tanárom adta fel ezt a feladatot, szerintem érdemes rajta elgondolkozni:
88. feladat: 10 kalóz szerzett 100 aranyat. Egymás közt el akarják osztani, úgy hogy a legkegyetlenebb kalóz osztja szét az aranyat, és ezt megszavaztatják. Ha a kalózok lagalább fele megszavazza, elosztják az ajánlat szerint. De ha a kalózok kevesebb, mint fele szavazza meg, a legkegyetlenebb kalózt vízbe dobják a nyílt tengeren, és a második legkegyetlenebb kalóz folytatja az elosztást. A kalózok egyformán inteligensek. Nincs köztük két egyformán kegyetlen. (A felosztó kalóz szavazata is beleszámít!)
Hány aranyat adjon magának a legkegyetlenebb kalóz, hogy biztosan ne dobják vízbe?
A feladatot lehet hogy nem fogalmaztam elég pontosan, de emlékezetből írtam le. Ha van valami kérdésetek írjatok!
|
|
|
|
| [405] nadorp | 2004-07-02 12:36:16 |
 Nem tudom,hogy szebb-e, de kicsit rövidebb.
Csináljunk az egyenletből egyenletrendszert:
log3(2x+1)=y és log2(3x-1)=y
azaz,
2x+1=3y
3x-1=2y
összeadva a két egyenletet 2x+3x=2y+3y. Mivel az f(x)=2x+3x függvény szigorúan monoton nő, ezért az előző egyenlőség csak x=y esetén teljesül, azaz
log3(2x+1)=x
2x+1=3x
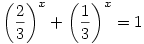
A fenti egyenletnek az x=1 megoldása,és másik nincs is, mert a bal oldalon egy szigorúan monoton csökkenő függvény áll.
|
| Előzmény: [404] Sirpi, 2004-07-02 11:50:23 |
|
| [404] Sirpi | 2004-07-02 11:50:23 |
 Nos, mivel eddig senki nem reagált senki a példára, beírom ide a ronda, favágós megoldásomat. Ha valaki tud szebbet, szóljon.
Legyen f(x)=log3(2x+1), g(x)=log2(3x-1). Olyan x-ek kellenek, amire f(x)=g(x).
Könnyű látni, hogy az x=1 megoldás, továbbá g(x) csak pozitív x-ekre van értelmezve. Ha ezek után megmutatjuk, hogy a közös értelmezési tartományon g(x) "gyorsabban nő", mint f(x), akkor készen is vagyunk, hiszen ebben az esetben az x=1-en kívül nem létezhet más megoldás.
Egyszerú átalakítással, felhasználva a logab=logcb/logca azonosságot, kapjuk, hogy 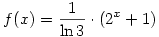 és és 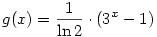 . .
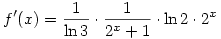
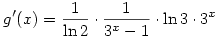
Mindkét derivált pozitív x>0 esetén, továbbá 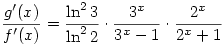 . Itt mindhárom tényező nagyobb, mint 1, vagyis minden x>0-ra g'(x)>f'(x), vagyis a g(x)-f(x) függvény szigorúan monoton nő. . Itt mindhárom tényező nagyobb, mint 1, vagyis minden x>0-ra g'(x)>f'(x), vagyis a g(x)-f(x) függvény szigorúan monoton nő.
|
| Előzmény: [403] lorantfy, 2004-06-30 06:50:07 |
|
| [403] lorantfy | 2004-06-30 06:50:07 |
 86. feladat: Oldjuk meg a köv. egyenletet a valós számok halmazán:
log3(2x+1)=log2(3x-1)
(Hegyi Lajos Emlékverseny 1999. 10.oszt.)
|
|
|
|
| [400] nadorp | 2004-06-28 10:18:27 |
 Újabb kísérlet a 85. feladatra.
Alakítsuk át az egyelet bal oldalát.
(x+y)2-4(x+y)+8y=13
(x+y-2)2=17-8y
Ha bevezetjük a z=x+y-2 jelölést, akkor (sajnos a frac nem működik)
y=(17-z2)/8 és
x=(z2+8z-1)/8.
Most már csak z-re kell kikötés. Látszik, hogy ha z páros, akkor y nem lehet egész, viszont ha z páratlan, akkor y - és így x is - egész lesz. Az egyenlet összes megoldása tehát a fenti két képlettel definiált x,y számok, ahol z tetszőleges páratlan szám.( pld x=8 y=-1 a z=5 esetén adódik)
|
| Előzmény: [397] lorantfy, 2004-06-28 09:19:12 |
|
| [399] Hajba Károly | 2004-06-28 09:57:14 |
 Kedves László és Péter!
Első ránézésre nem tűnt olyan érdekesnek, mint menet közben kiderült. :o)
Megoldás a 85. feladatra:
(1) (x+y)2-4(x-y)=13
Rendezzük y-ra az (1) egyenletet:
y2+2(x+2)y+x2-4x-13=0
azaz
y1,2=-(x+2) GYÖK(8x+17) GYÖK(8x+17)
Akkor kapunk egész megoldást, ha a gyök alatti érték négyzetszám. S itt meglepő fordulat következik. :o) Legyen
8x+17=(2n+1)2
 (n>1) (n>1) N+-re N+-re x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o) x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o)
Innen a képleteket (x=..., y=...) nem tudom beírni, mivel nem jó jelenleg a TeX értelmezője. :o(
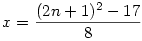
Később folytatom.
HK
|
| Előzmény: [395] lorantfy, 2004-06-27 12:54:37 |
|
| [398] nadorp | 2004-06-28 09:55:12 |
 Kedves László !
Teljesen igazad van, de mire ezt észrevettem, már Te is. A megoldásom teljesen rossz, elkapkodtam és elszámoltam. De vam másik, mindjárt leírom, ha még nem késő.
|
| Előzmény: [397] lorantfy, 2004-06-28 09:19:12 |
|
|
| [396] nadorp | 2004-06-28 08:35:24 |
 Úgyis régen szóltam hozzá. Megoldás a 85. feladatra.
Egészítsük ki az egyenlet bal oldalát teljes négyzetté.Ekkor
(x+y)2-4(x-y)+4(x-y)2=13+4(x-y)2
[x+y-2(x-y)]2=13+(2x-2y)2
(x-3y)2-(2x-2y)2=13
Két négyzetszám különbsége csak a 49 és 36 esetén lesz 13, ezért a
x-3y= 7 7
x-y= 3 3
egyenletrendszereket kell megoldani. Látható, hogy a négy egyenletrendszerből csak y=2 x=-1 esetén kapunk megoldást.
|
| Előzmény: [395] lorantfy, 2004-06-27 12:54:37 |
|
| [395] lorantfy | 2004-06-27 12:54:37 |
 85. feladat: Oldjuk meg az egész számok halmazán a következő egyenletet:
(x+y)2-4(x-y)=13
|
|
| [394] Lóczi Lajos | 2004-06-24 12:55:57 |
 Kedves Mihály!
Ahhoz, hogy egy valós függvény deriváltját a 0-ban kiszámolhassuk, szükséges, hogy a függvény értelmezve legyen legalább egy 0-hoz torlódó pontsorozat mentén.
Nem beszélhetünk tehát "csak az origóban deriválható függvényről, amely ott ráadásul kétszer is deriválható", hiszen a második derivált 0-beli értékének kiszámításához az előző bekezdés értelmében ismernünk kellene az első derivált értékeit egy 0-hoz torlódó pontsorozat mentén. Mivel azonban az első derivált csak a 0-ban van definiálva, ez nem lehetséges.
A válasz tehát, hogy ilyen függvény nincs.
|
| Előzmény: [393] Fálesz Mihály, 2004-06-18 14:06:40 |
|






 +sinSBC
+sinSBC
 GYÖK(8x+17)
GYÖK(8x+17)  (n>1)
(n>1) N+-re
N+-re x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o)
x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o) 