| [443] V. Dávid | 2004-08-31 17:52:32 |
 "Mi a helyzet akkor, ha nincsen kalapjuk meg kavicsuk, csak papíruk és ceruzájuk?" Ugyanaz a helyzet mint akkor, amikor kavicsokat dobáltak. Mondjuk 1. annyi szakaszt húz, ahány éves, aztán behajtja a lapot. 2. pedig itt folytatja a vonalhúzogatást. A lap visszahajtása után a szakaszok határa nem látható. (Feltesszük, hogy eközben más nem néz a lapra.)
|
| Előzmény: [425] Csimby, 2004-07-20 00:58:53 |
|
|
| [441] lorantfy | 2004-08-19 17:05:54 |
 93.feladat: Oldjuk meg az egyenletrendszert!
2x2+y+2x+y2=8
sqrtx+sqrty=2
|
|
|
| [439] joe | 2004-08-07 18:11:07 |
 92. feladat: Van két piros, két fehér és két zöld golyónk. Az azonos színűek közül az egyik 100, a másik 101 grammos. Egy kétkarú mérleg segítségével, mérősúlyok nélkül, két méréssel állapítsuk meg mindegyik golyó súlyát!
|
|
| [438] Káli gúla | 2004-08-05 23:06:09 |
 Sziasztok!
Megoldás a 71. feladatra.
Színezzük pirossal és kékkel a sakktáblát. Elég belátni, hogy vagy (a) van minden oszlopot érintő piros út, vagy (b) van minden sort érintő kék út, mert (a) esetben a piros, (b) esetben a kék rész járható végig.
Nyilván feltehetjük, hogy nincsen sem egyszínű sor, sem egyszínű oszlop. Ha bármelyik két szomszédos oszlopnál a piros mezők közt van valahol "átjárás", akkor az (a) eset teljesül, ezért feltehetjük, hogy az i-edik oszlop piros mezőiről nincs átjárás az (i+1)-edik oszlop piros mezőire. Ekkor ez a két oszlop tartalmazni fog egy (b) szerinti kék utat, mert egyrészt az i-edik oszlop piros pontjai mellett az (i+1)-edik oszlopban kék pontok vannak, tehát a két oszlop kék színű pontjai az összes sort lefogják, másrészt az i-edik oszlop nem egyszínű, így valamelyik piros mezőjének van függőleges kék szomszédja is, ami a vízszintes kék szomszédjával átlósan összeköthető.
|
|
| [437] Suhanc | 2004-08-02 13:00:22 |
 Kedves Csimby!
Bocsi, hogy ilyen "jó" a reakcióidőm... táborozni voltam. A négy dimenziós kockának csak a megoldását tudom, a füzetemet meg még nem találtam meg, amibe leírtam!;)
De keresem...:)
A Gordiuszon mesélte egy srác, hogy a sulijában páran összefogva elemezték a SET-et, olyan k és l paraméterekre, hogy k a tulajdonságok száma, l egy tulajdonságon belül a lehetőségek száma. Erre is sikerült asszem megadniuk a maximális húzható lapot...
A fodrászos feladathoz pedig 2 dolog jutott eszembe:
1. Egy másik megoldásötlet: Hívjuk vissza Gedeon bácsit, de előtte a három nő beszéljen meg egy X számot! Majd egyenként mondják meg neki életkor +X értékét. Ekkor Gedeon bácsi tudja a sorrendet, de nem tudja a valós életkort!:)
2. Egy kérdés: Összejátszhat-e bármely 2 nő a harmadik életkorának megismeréséért? / szóval kibeszélik-e;)) / Mert, ha feladatod azt kéri, még öszejátszással se lehessen kideríteni, akkor az eddigi két ötletem nem volt jó...:)
|
| Előzmény: [436] Csimby, 2004-07-23 18:36:33 |
|
| [436] Csimby | 2004-07-23 18:36:33 |
 Helló!
Én is ott voltam a táborban, de erre sajnos nem emlékszem ;-( így érdemes engem tanítani. Na de most én is a SET kapcsán kezdtem el ezzel foglalkozni! A max. már megvan általánosan csak bizonyítani még nem sikerült, a SET-re sem(SET-nél 4 dimenziós kocka kell)(négyzetre megvan), de már érzem, hogy meglessz a SET is :-) Ha emlékszel vmire amit a táborban mondtak róla légyszi írd meg (csajbok@dpg.hu)! Nagyon jó az a játék és érdekes problémákat vet fel...
|
| Előzmény: [434] Suhanc, 2004-07-23 13:31:28 |
|
| [435] Suhanc | 2004-07-23 13:46:42 |
 Egy ötlet a 90.Feladat-hoz:
Legyen a három nő 1. 2. 3., életkoruk A;B;C. 1. gondol egy pozitív egész X számra, és megsúgja 2.-nek az A+X összeget. 2. megsúgja 3.-nak az A+B+X összeget. 3. megsúgja 1.-nek az A+B+C+X összeget.
Ekkor 1. Ismeri B+C+X értékét. Megsúgja 2.-nak a B+C+X összeget. Mivel 2. Ismeri saját életkorát, így ismeri C+X összeget.
Mivel 2. ismeri A+X és C+X összegeket, így ismeri C-A értékét. E különbség előjele meghatározza, hogy A vagy C az idősebb. Ezt B hangosan bemondja.
Ezután B, majd C gondol egy számot,és így 3kör alatt három egyenlőtlenséghez jutunk, melyekben az életkorok szerepelnek, és így egyértelműen meg tudjuk állapítani a sorrendet.
Megj. ez a megoldás csak akkor működhet, haténylegnem egyidősek... de ha mondjuk pontosítunk, és A= 10000000000000000000000000*8születési év)+1000000000*(születés hónapja)+100000*(nap) +1000*(óra)+(perc) B=...
akkor nagy valószínűséggel nem lesz A=C ;)
Egy extrémebb kérdés, bár nem gondoltam át, hogy van-e egyáltalán megoldása...
Mindhárman a búra alatt ülnek, és ordibálnak... tehát nincs suttogás, mindenki hall mindent, se papír, se toll! most mit lehet csinálni?
|
|
| [434] Suhanc | 2004-07-23 13:31:28 |
 Kedves Csimby!
Ezzel a feladattal a tavalyi Montágh- Hraskó-Kós féle táborban talákoztam, a SET nevű játék kapcsán. :)
Akkor ott ezt 3D-ben, és az eredeti játékra vonatkozóan is vizsgálta az előadó...
|
|
| [433] Csimby | 2004-07-23 12:12:10 |
 Elnézést, nem voltam elég világos, tehát átlónak tekintem pl. a következő ábrán mind a 3 különböző színnel jelölt 3-as csoportot.
|
 |
|
| [432] Sirpi | 2004-07-23 11:36:29 |
 Bocs, nem olvastam el a feladat legutolsó mondatát... Szóval nxn-es esetben mind a 2n átlót kéne figyelni, szóval rossz, amit írtam.
Ebéd alatt majd kitalálom :-)
|
| Előzmény: [431] Sirpi, 2004-07-23 09:29:27 |
|
| [431] Sirpi | 2004-07-23 09:29:27 |
 Ez megy nxn-esre is, ha n 3, azaz be lehet bizonyítani, hogy n(n-1) a maximum (több nem lehet, mert akkor a skatulyaelv miatt lenne teli sor). 3, azaz be lehet bizonyítani, hogy n(n-1) a maximum (több nem lehet, mert akkor a skatulyaelv miatt lenne teli sor).
Vázlat:
o+++++++
++++++o+
+++++o++
++++o+++
+++o++++
++o+++++
+o++++++
+++++++o
Mj: n=1-re 0, n=2-re 1 a maximum.
|
| Előzmény: [429] Csimby, 2004-07-23 00:19:20 |
|
| [430] Suhanc | 2004-07-23 08:54:47 |
 Kedves Csimby!
A 91. Feladat-ot nem értem...
/így jártam;) /
Az nem világos, hogy miért emeled ki a nem főátlókat, hiszen azokban nincs 3 mező, értelemszerűen nem is tudunk majd ott 3-at kiválasztani.
Ha a feladat tényleg így szól, azt hiszem, ez egy lehetséges megoldás:
Tekintsük a négyzet sorait! Minden sorban legfeljebb 2 kiválasztott négyzet lehet, tehát legfeljebb 6- ot választhatunk ki. 6-ra pedig készíthető ilyen konstrukció:
Ha megszámozzuk a 9 mezőt a számológépek klaviatúrájának megfelelően (bocsánat, rajzolni még most sem tudok) , akkor válasszuk ki a 2,3,4,6,7,8 mezőket.
Ekkor minden sorban és oszlopban , valamint az egyik főátlóban 2 kiválasztott mező van, míg a másik főátló üres.
|
| Előzmény: [429] Csimby, 2004-07-23 00:19:20 |
|
| [429] Csimby | 2004-07-23 00:19:20 |
 91.feladat Ez nem nehéz, csak arra vagyok kíváncsi, hogy ki hogyan bizonyítja:
Van egy 3×3-as négyzetünk. Legfeljebb hány mezőt tudunk úgy kiválasztani, hogy semelyik oszlopban, sorban és átlóban se legyen 3 a kiválasztott mezők közül (átló alatt nem csak a két fő átlót, hanem mind a 6-ot értem).
|
|
| [428] Csimby | 2004-07-21 15:40:07 |
 Igazad van, pl. A nem tudhatja meg A és B vagy A és C kor különbségét. Az összehasonlítást tehát vagy úgy kell elvégezni, hogy csak az derüljön ki melyik az idősebb ne az, hogy mennyivel. Vagy pedig ha pl. A és B korkülönbségét akarjuk megtudni, akkor azt C vizsgálja (ő megtudhatja mennyi a különbség, konkrét infója ebből neki nem lesz és nem árulja el csak azt, hogy ki az idősebb), persze C+A-t és C+B-t nem hasonlíthatja össze C, hiszen akkor megtudná A és B korát. Az egyenlőséget egyébként kizárhatjuk, ha a korhoz hozzávesszük, a hónapot, napot, percet.
|
| Előzmény: [427] Sirpi, 2004-07-21 13:23:30 |
|
| [427] Sirpi | 2004-07-21 13:23:30 |
 Nem kötözködésből, csak érdekel:
Arról volt szó, hogy úgy akarják meghatározni az életkor sorrendet, hogy a másik két hölgy számára ne derüljön ki semmilyen információ a tényleges korukról. Igazából a korok nem is mindig derülnek ki, de mindenki tudni fogja, hogy hány év korkülönbség van a másik kettő között. Wz ezért plusz információ a sorrendhez képest. Azért megengedjük?
(Példa: kiderül, hogy az első hölgy a legidősebb, és a másik kettő pedig megegyező korú. Ekkor mind a hárman explicite tudni fogják az életkorokat is.)
|
|
| [426] Hajba Károly | 2004-07-20 16:39:38 |
 Kedves Csimby!
Te még korodnál fogva nem ismerheted Gedeon bácsi főhajszobrászt, a nők bálványát, de benne minden nő megbízik és két dajer között mindhárom nő a fülébe súgja a korát és ő sorba rakja őket. :o)
Nos, ha a papírra vetett számokat vagy egyéb információhordozót más nem nézheti meg, csak ők, akkor egyelőre még nem tudom az eljárást. De még gondolkozom rajta egy kicsit.
Üdv: HK
|
| Előzmény: [425] Csimby, 2004-07-20 00:58:53 |
|
|
| [424] Hajba Károly | 2004-07-19 23:55:42 |
 Megpróbálom egy kicsit egzaktabbul előadni a feladatmegoldásomat, s ellenézést a slendriánságért. :o)
Legyen a 3 nő életkora A, B, C és rendre összehasonlítják a következők szerint. 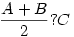 ; ; ; ;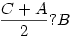 . .
A ? jel helyén <,>,= relációk lehetségesek, így összesen 27 féle eredmény képzelhető el, de ebből 14 féle állapot kizárt.
Egyik valós állapot, mikor mindhárom egyenlő, ekkor egyforma idősek. Ezenkivül már csak olyan állapot lehetséges, mikor legalább egy > és legalább egy < jel is szerepel. Az a nő, ki egyedül kisebb vagy egyedül nagyobb, egyúttal a hármójuk közül a legfiatalabb ill. legidősebb is. A másik kettő ilyenkor úgy tudja eldönteni a sorrendet, hogy megnézik a harmadikkal együtt az övék több vagy a másik. Pl. ha A már ismert akkor (A+B)?(A+C). Ezek az értékek már egyébként is ismertek.
Előfordul olyan állapot is, mikor egy legkisebb és egy legnagyobb adódik egyszerre, ekkor a harmadik egyenlő, s ebből logikusan következik a sorrend is. Pl. 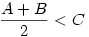 ; ;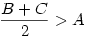 ; ;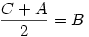 . Ekkor a sorrend A<B<C. . Ekkor a sorrend A<B<C.
HK
|
| Előzmény: [423] Csimby, 2004-07-19 22:31:52 |
|
| [423] Csimby | 2004-07-19 22:31:52 |
 "Ha két ilyen is van, akkor az egyik kisebb, a másik nagyobb, a harmadik egyenlő." - Egyenlő mivel?
"A két egyformán kisebb vagy nagyobb kettő megnézi, hogy az előbbivel együtt több vagy kevesebb kaviccsal rendelkeznek, s ebből következtethetnek a koruk viszonyára." - Mi az előbbi?
Bocsánat, nem csak kötözködés, tényleg nem értem.
|
| Előzmény: [422] Hajba Károly, 2004-07-19 18:40:30 |
|
| [422] Hajba Károly | 2004-07-19 18:40:30 |
 a 90. feladathoz:
Mindhárom nő párosával annyi kavicsot dob egy kalapba ahány éves, s a harmadik megnézi, hogy a kalapban lévő kavicsok felénél az ő kora kevesebb, több vagy egyenlő. Így három vizsgálatot végeztek.
Aki kora egyedül kevesebb vagy több a kalapban lévő kavicsok felénél, az a legfiatalabb vagy legidősebb. Ha két ilyen is van, akkor az egyik kisebb, a másik nagyobb, a harmadik egyenlő. Ebből már adódik a sorrend.
A két egyformán kisebb vagy nagyobb kettő megnézi, hogy az előbbivel együtt több vagy kevesebb kaviccsal rendelkeznek, s ebből következtethetnek a koruk viszonyára. Akár egyidősek is lehetnek.
Meg egy lehetőség adódik, amikor mindhárom eset egyenlőt ad. Ekkor egyenlő korúak.
A három mérésből elvileg 27 féle lehetséges kimenet lehet, de ebből 14 féle lehetetlen.
Üdv: HK
|
| Előzmény: [421] Csimby, 2004-07-19 13:05:08 |
|
| [421] Csimby | 2004-07-19 13:05:08 |
 Még régebben mondta egy barátom, aznap amikor egy orvosi vizsgálat miatt 1/2 órát kellett mozdulatlanul feküdnöm. Mire vége lett megvolt :-). Mikor feladtad, a megoldásra már nem emlékeztem csak arra, hogy egyszer már megcsináltam. Bocsánat, hogy ilyen gyorsan lelőttem, pedig már ismertem, de ez az egyik kedvenc példám!
90.feladat A fodrásznál ül 3 nő és szeretnék egymást koruk szerint növekvő sorrendbe rendezni. Ugyanakkor egyik sem szeretné, hogy a sorrenden kívül bármilyen információ is kiderüljön a koráról, a végén tehát semmit sem fognak tudni a másik életkoráról csak az életkoruk sorrendjét. Hogyan csinálják?
|
| Előzmény: [420] lorytibi, 2004-07-19 11:12:08 |
|
| [420] lorytibi | 2004-07-19 11:12:08 |
 Ez szép volt Csimby!
Ismerted a feladatot, vagy csak ilyen könnyű volt?
Nekem nagyon nehéznek tűnt, nem gondoltam volna, hogy egy ilyen egyszerű trükkel meg lehet oldani.
|
| Előzmény: [419] Csimby, 2004-07-19 00:43:26 |
|
| [419] Csimby | 2004-07-19 00:43:26 |
 Kiválasztassz 100-at tetszőlegesen és megfordítod! Ez a 100 db. lesz az egyik csoport a másik pedig az összes többi. Bővebb indoklást direkt nem írok, gondoljátok végig!
|
| Előzmény: [418] lorytibi, 2004-07-17 20:01:28 |
|










 3, azaz be lehet bizonyítani, hogy n(n-1) a maximum (több nem lehet, mert akkor a skatulyaelv miatt lenne teli sor).
3, azaz be lehet bizonyítani, hogy n(n-1) a maximum (több nem lehet, mert akkor a skatulyaelv miatt lenne teli sor). 