| [56] Lóczi Lajos | 2003-11-12 19:38:44 |
 Tetszetős ez a megoldás... Kérdezném, kinek mi a véleménye e megoldás alábbi határesetéről: az északi sarkponttól 1 km-re délfelé kezdi meg az útját; 1 km-t északra haladva bejut az É sarkra, kelet felé onnan nem tud (mert nem lehet) haladni, tehát nem mozdul, majd dél felé 1 km-t ballag és visszajut a kezdőpontba.
Azaz, elfogadjuk-e "1 km keletre haladásnak" azt, ha valahol nem lehet kelet felé haladni.
Másik megjegyzésem: hogyan lehetne (formálisan, esetleg rajz nélkül) bizonyítani, hogy több lehetséges útvonal nincsen? (Hiszen az első megoldás is meggyőzőnek tűnt.)
Azzal is érdekes -- és minden bizonnyal sokmegoldású -- feladatokat lehetne gyártani, ha pl. a megtett távolságok összemérhetők/meghaladják a bolygó (fél)kerületét.
|
| Előzmény: [55] Sirpi, 2003-11-12 14:58:22 |
|
| [55] Sirpi | 2003-11-12 14:58:22 |
 Lorybetti: a feltételek csak úgy teljesülhetnek, ha a medve kezdetben pontosan a déli sarkponton áll, majd halad É fele, K fele és D fele és visszajut a déli sarkpontra.
Nem csak így lehet... Vegyünk az északi sarkpont közelében egy olyan szélességi kört, aminek kerülete osztja az 1km-t, és a kiindulópont ettől 1km-rel délre legyen. Ebben az esetben az É, K, D út triviálisan a kezdőpontba vezet, és akkor mégse pingvint találtunk :-) Vagyis az eredeti feladat is értelmes, nem kell permutálni az irányokat.
S
|
| Előzmény: [50] lorybetti, 2003-11-10 22:23:48 |
|
|
|
| [52] Bubu | 2003-11-12 01:14:45 |
 Rendbonto leszek, elnezest erte... Szoval a billiardgolyos feladat (amit egyebkent anno GY peldakent lekuzdottem:)) egy kulonleges matematikai kepzettseggel nem biro (erettsegi), de egyebkent feletteb intelligens rokonomat "megihlette". Azt allitja, hogy 5 meressel 12 golyobol ki tud valasztani 2 db eltero tomegut! Precizebben: van 12 kulsore egyforma golyo. 10 tomege megegyezik, kettoje elter (hogy milyen "iranyban" es mennyire, azt nem tudjuk). Egy ketkaru merleg segitsegevel valasszuk ki a ket kulonc golyot ot meressel. A megoldasrol sejtelmem sincs, de a hetvegen fogok vele foglalkozni. Aki barmilyen reszeredmenyt/otletet tud, az mailezzen legyen szives!
|
|
| [51] lorantfy | 2003-11-11 23:00:51 |
 A tevés feladat megoldása:
Az osztószámok: k , l, m, a tevék száma: n és k < l < m < n.
A végakarat teljesítésének szükséges feltétele a kölcsönkért 1 tevével:
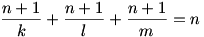
Mindkét oldalt elosztva (n+1) –el és 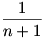 –et mindkét oldalhoz hozzáadva: –et mindkét oldalhoz hozzáadva:
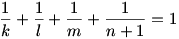
Ezt az egyenletet kell megoldanunk a 0 < k < l < m < n+1 : egész számok feltétellel.
Látszik, hogy k = 2, ugyanis k = 3 esetén a lehető legkisebb l, m, n+1 értékekre is az összeg 1-nél kisebb:
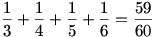
Már csak három ismeretlenünk van:
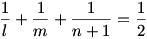
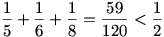
emiatt l lehetséges értékei: l = 3, l = 4
Kezdjük l = 3–mal:
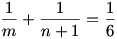
és 6 < m < 12 ( az összeg felének reciprokánál kisebb)

Tehát (m-6) osztója 36-nak.
m = 7, n+1 = 42, n = 41 jó megoldás,
m = 8, n+1 = 24, n = 23 jó megoldás,
m = 9, n+1 = 18, n = 17 jó megoldás,
m = 10, n+1 = 15, n = 14 NEM jó megoldás, mert 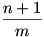 nem egész szám. nem egész szám.
l = 4 a következő eset
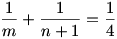
és 4 < m < 8 ( az összeg felének reciprokánál kisebb)
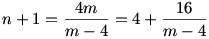
Tehát (m-4) osztója 16-nak.
m = 5, n+1 = 20, n = 19 jó megoldás,
m = 6, n+1 = 12, n = 11 jó megoldás.
Összesen 5 megoldást találtunk!
|
|
| [50] lorybetti | 2003-11-10 22:23:48 |
 Kedves Fálesz Mihály!
Egyetértek Veled, így szeretném csökkenteni a megoldatlan példák számát.A medvés példa- Fizban 22.es hozzászólása A szöveg így szólt: "Elindul Észak felé, és megy 1 km-t. Ezután elfordul Kelet felé, és megint megtesz 1 km-t. Aztán Délnek fordul, és -ki gondolta volna- megtesz még 1 km utat. Ezután a medve visszajut a P pontba."
A feladat megoldása: a feltételek csak úgy teljesülhetnek, ha a medve kezdetben pontosan a déli sarkponton áll, majd halad É fele, K fele és D fele és visszajut a déli sarkpontra. Tartok töle, hogy Fizban rosszul írta az irányokat, mert így a medve fekete-fehér színű és Pingvin névre hallgat. Ha jegesmedvéről lenne szó-ami persze fehér: az irányok sorrendje: D, K és É vagy K, É, D vagy É, D, K (utóbbi két esetben csak érinti az északi sarkpontot)
Értékes megjegyzés: A medve olyan gömbi háromszögben mozog, melynek minden szöge derékszög. Lehet hogy Bolyait is ez ihlette meg?
|
|
| [49] Fálesz Mihály | 2003-11-10 18:10:51 |
 Sziasztok,
Kicsit kezdenek elburjánzani a meg nem oldott feladatok. Pillanatynilag a következőkre nincs még teljes megoldás:
-- 2. feladat (9 pont), 2. hozzászólás
-- 3. feladat (emberevők) [3]
-- 5. feladat (100 láda pénz) [6]
-- milyen színű a medve [22]
-- tevék [26]
-- Rubik-hasáb [43]
-- mekkora az EDB szög [46-47]
Összesen 7, ami túl sok. Azt javaslom, hogy most egy darabig ne írjunk új feladatokat, inkább ezekere lássunk megoldást, és a továbbiakban is törekedjünk arra, hogy ne legyen egyszerre - mondjuk - háromnál több megoldatlan feladat.
F.M.
|
|
| [48] Sirpi | 2003-11-10 14:18:59 |
 Ez a szummafelcserélés tökéletes megoldás, gratula, én is így csináltam (mellesleg azért nem így adtam fel, mert így sokkal könnyebb, csupán a 2, 3, 5, 8 kitevőket kivéve szerintem nehezebb feladatot kapunk.
|
| Előzmény: [40] Pach Péter Pál, 2003-11-07 23:14:59 |
|
| [47] lorantfy | 2003-11-10 11:21:06 |
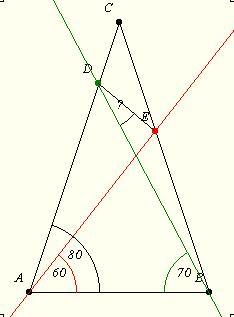
 Egy ábra a lenti feladathoz. (Imádom az Euklides programot!)
|
 |
|
| [46] jenei.attila | 2003-11-10 10:44:46 |
 Egy geometria feladat: Az ABC egyenlő szárú háromszög AB alapon fekvő szögei 80 fokosak. A-ból az alappal 60 fokos szöget bezáró egyenes a BC szárat E pontban, B-ből az alappal 70 fokos szöget bezáró egyenes az AC szárat D pontban metszi. Mekkora az EDB szög?
|
|
| [45] Hajba Károly | 2003-11-10 01:19:09 |
 > köszönöm, hogy ilyen szép táblázatos formában feltetted az eredményt
Tanulom a TeX-et. :o)
> Te biztosan emlékszel még a RUBIK kockára
Mi az, hogy emlékszem! Engem a gimi 3. osztályában ért (ma 11. o.), s a kockám nemegyszer a tanári asztalon vészelte át az óra második felét több más kockával egyetemben. Így az ábrád öt percnyi tanulmányozása után rájöttem a "trükk"-re, de hagyok mást is gondolkodni.
|
| Előzmény: [43] lorantfy, 2003-11-08 15:50:59 |
|
| [44] Lóczi Lajos | 2003-11-09 16:21:43 |
 Valóban, ez így szép és jó. Utólag természetesen a "mi" formulánkat is megtaláltam, pl. a http://mathworld.wolfram.com/RiemannZetaFunction.html oldalon ez a (23)-as formula :-) Érdemes megnézni, van néhány szép ábra (és csaknem 100 egyéb dzeta-képlet)...
|
| Előzmény: [40] Pach Péter Pál, 2003-11-07 23:14:59 |
|
| [43] lorantfy | 2003-11-08 15:50:59 |
 Kedves Károly!
Gratulálok a megoldáshoz és köszönöm, hogy ilyen szép táblázatos formában feltetted az eredményt!
Te biztosan emlékszel még a RUBIK kockára és remélem, hogy a fiatalabbak is ismerik. Nekem nagy sikerélmény volt, hogy meg tudtam oldani. 3 napom ment rá egy téli vizsgaidőszakban és meg is lett az eredménye, 4-es lett az analízis vizsgám… A következő nyáron Angliában jártam és ott lehetett kapni a Rubik kocka mindenféle változatát. Vettem is egy nyolcszög alapú hasáb alakút és összekeverés után a begyakorolt transzformációkkal próbáltam visszaforgatni az alaphelyzetbe. Rejtélyes módon az alábbi eredményre jutottam: egy élközépen lébő kocka megfordult a többi mind a helyére került. 9. feladat : Hogyan lehetséges ez?
|
 |
|
|
| [41] lorantfy | 2003-11-08 00:39:03 |
 Kedves Fórumosok !
Örülök, hogy ilyen sokan foglalkoztatok a biliárdgolyós példával, még idemásolok egy megoldást, ami felhasználja ugyan az előbbi mérés eredményét, de talán annak aki később idetéved érthetőbb:
A 12 golyót 3 4-es csoportra bontom.
OOOO OOOO OOOO
Két 4-es csoportot összehasonlítok a mérleggel (1. mérés)
OOOO -- OOOO
1.1. Egyenlők: ekkor a maradék 4 között van az eltérő
OOOO = OOOO HHHH
Veszek 2-t az első 8 golyó közül (ezek jók) és 2-t a maradék 4-ből
OO -- HH HH
Összemérem őket (2. mérés),
1.2. Ha lebillen a mérleg akkor a mérlegen lévő kettő (HH) közül a 3. méréssel eldöntöm melyik az eltérő golyó.
1.3. Ha egyenlő a 2. mérés eredménye akkor a nem mért 2 közül (HH) döntök a 3. méréssel. (Egyiket összemérem egy jó golyóval)
2.1. Ha a két 4-es csoport összemérésekor lebillen a mérleg. Ekkor amerre lebillent azt a 4 golyót N betűvel jelölöm ( ezek között lehet egy nehezebb)a másik oldalon lévő 4-et K betűvel jelölöm (ezek között lehet egy könnyebb)
Pl.: KKKK < NNNN OOOO
2.2. Bal oldalra felteszek a mérlegre 3 db K jelű golyót és 1 db N jelűt, jobb oldalra pedig 1 db (a megmaradt) K jelűt és a 3 db biztosan jó golyót. (Még 3 db N jelű és egy jó (O) marad ki)
KKKN -- KOOO NNN O
Nézzük az eseteket:
3.1. Ha a mérleg jobbra billen le. Ekkor a bal oldali 3 K közül 1 golyó könnyebb.
KKKN < KOOO NNN O
Ezek közül egy méréssel tudok dönteni, hiszen tudom, hogy a hibás golyó könnyebb. Kettőt összemérek, amelyik felemelkedik az a hibás. Ha egyenlő a kettő összemért, akkor a 3. a hibás golyó.
3.2. Ha a mérleg egyensúlyban marad akkor a kimaradt 3 db N jelű golyó
KKKN = KOOO NNN O
között van egy nehezebb, amit a 3. méréssel az előzőhöz hasonlóan el lehet dönteni.
3.3. Ha a mérleg balra billen ki, akkor ezt okozhatja a bal oldali N jelű golyó vagy a jobb oldalon lévő K jelű golyó.
KKKN > KOOO NNN O
Ezt a 3. méréssel könnyen el lehet dönteni, ha pl. a K jelűt összemérem egy jó golyóval. Ha felemelkedik akkor ez a hibás, ha egyenlők, akkor az N jelű.
|
|
| [40] Pach Péter Pál | 2003-11-07 23:14:59 |
 A 8. feladatra írok megoldást, úgyhogy, aki még nem oldotta meg (és szeretne rajta gondolkozni), ne olvassa tovább. Tekintsük a következő átalakításokat:
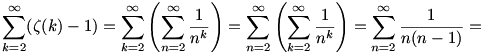
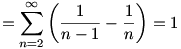
Pozitív számokat összegzünk, és a határérték valóban létezik (olvassuk az átalakításokat hátulról visszafelé), így nem "csaltunk", amikor megcseréltük a két szummát. Ezen kívül a mértani sor összegképletét, és egy ún. "teleszkópos trükköt" alkalmaztunk.
Az előbb bizonyított állítás nyilvánvaló következménye, hogy
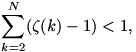
ugyanis az előbbi összegnek van olyan tagja, ami ebben az összegzésben nem szerepel. (Mint már megállapítottuk, minden tag pozitív: 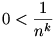 ) )
Pach Péter Pál
|
| Előzmény: [30] Lóczi Lajos, 2003-11-05 23:59:16 |
|
| [39] lorantfy | 2003-11-07 09:56:01 |
 A biliárdgolyós példa alábbi megoldását Gáti Beatrix küldte nekem.
|
 |
|
| [38] lorantfy | 2003-11-06 23:19:20 |
 Kedves Csillag! Nagyon szép a megoldásod, gratulálok! Holnap felteszek hozzá egy táblázatot, hogy mikor melyik golyó jön ki, igy mindenki ellenőrizheti, hogy jó is. Elemben a tevés példán gondolkodók még keresgélhetnek, ha van idejük, mert én 5 megoldást találtam.
|
|
| [37] Csillag | 2003-11-06 16:02:59 |
 A billiárdgolyós probléma mindkét nehezített változatát megoldja a következő három mérés. Ezzel 12 golyó esetén meghatározható, hogy melyik volt hibás és hogyan, 13 golyó esetén pedig, hogy melyik volt hibás: 1.mérés: (x1,x2,x3,x4) összehasonlítása (x5,x6,x7,x8)-cal 2.mérés: (x1,x2,x5,x11) összehasonlítása (x3,x6,x9,x10)-zel 3.mérés: (x1,x6,x9,x11) összehasonlítása (x3,x4,x7,x12)-vel
|
| Előzmény: [20] Kós Géza, 2003-11-05 12:21:41 |
|
| [36] Kós Géza | 2003-11-06 14:24:35 |
 Kedves Csimby,
Amit írtatok, az mindenképpen megérdemel egy fél Túró Rudit, de jobb lenne egy szép, világos, kerek megoldássá átírni. Ehhez pontosabban kell kezelni a falvak és a hittérítők lehetséges állapotait.
|
| Előzmény: [23] Csimby, 2003-11-05 18:21:35 |
|
| [35] lorantfy | 2003-11-06 14:18:01 |
 Az eredeti tevés példa úgy szólt, hogy 11 tevét örökölnek és hogyan oszthatnák el ha a legidősebb felét, a középső harmadát, a legkisebb hatodát örökölte. És a bölcs kádi javaslatára kölcsönkérnek egy tevét, amit az osztozkodás után vissza is adnak.
|
|
|
|
| [32] Hajba Károly | 2003-11-06 12:31:28 |
 A 7. feladathoz:
Először is elnézést mindenkitől, de még nem sikerült elmélyedni a TeX-ben, így annak lehetőségeit most nem használom ki. (De ami késik, nem múlik.)
Mivel a tevék számához még 1-t hozzáadva el tudták osztani kényelmesen és még meg is maradt a kölcsönteve, ezért a K, L, M számok reciprokösszege alulról közelíti az 1-t, de nagyobb mint a legkisebb elérhető N-re N/(N+1)=0,9; ahol N=2+3+4=9. (Lehet ennél finomabban is lehatárolni.)
Tehát azokat a számhármasokat kell megvizsgálni, melyek reciprokösszege ebbe a tartományba esik. K=2, mivel a 3, 4, 5 számhármasra 0,78..; továbbá 2, 4, 5 számhármasra 0,8666... jön ki, mint alsó korlát, másrészről 2, 3, 6 számhármasra 1,00 jön ki, mint felső korlát. Én a két számhármas között két megoldást találtam:
K=2, L=3, M=7, N=41
K=2, L=4, M=6, N=11
Hajba Károly
|
| Előzmény: [26] lorantfy, 2003-11-05 21:34:18 |
|