| [569] matekos04 | 2004-11-09 17:52:26 |
 113 feladat. Udv. mindenkinek!
A feladatom igy szol:
Tegyuk fel hogy van egy digitalis orank. Hany olyan idopont van egy nap alatt (24 h),hogy ha fejtetore allitjuk az orat ugyanazt a szamot kapjuk meg?
|
 |
|
| [568] Maga Péter | 2004-10-28 09:39:55 |
 112. feladat (a 108. feladat folytatása):
Határozzuk meg minden n>1-re azokat az a1,a2,...,an n-eseket, ahol minden ai 0 vagy 1, és
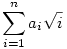 racionális! racionális!
|
|
| [567] Sirpi | 2004-10-22 10:34:40 |
 Megkerestem az ominózus cikket. Úgy tűnik, egyszerűen lemaradt az egyik nyitó zárójel. Az állítás azt mondja ki, hogy minden h>0-hoz van olyan N, hogy minden n>N-re el lehet helyezni legalább 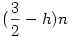 pontot a megadott tulajdonsággal. pontot a megadott tulajdonsággal.
|
| Előzmény: [566] Hajba Károly, 2004-10-22 10:02:38 |
|
| [566] Hajba Károly | 2004-10-22 10:02:38 |
 Megtaláltam a jelzett megoldást a Kömal archivumban 1998/2 66-67. o.
A megj/4. pontban szereplő (3/2)-h)n képlet, mely feltehetőleg nyomdaszedési hiba, értelmezhetetlen. Mi lehet a helyes képlet?
HK
|
| Előzmény: [565] Kemény Legény, 2004-10-21 23:34:45 |
|
|
|
| [563] Hajba Károly | 2004-10-19 15:22:00 |
 Az előző két feladatot egy hálón fellelt gyűjteményből emeltem át. Eredetüket a "közreadója" sem ismeri (Pósa, régi Kömal, ...? :o)
HK
|
|
| [562] Hajba Károly | 2004-10-19 15:19:35 |
 111. feladat:
Tetszőleges n pozitív egészre jelölje f(n) az n szám fordítottját tízes számrendszerben. (Például f(1994)=4991, f(5200)=25.) Keressük meg azokat a pozitív egész k számokat, amelyekre teljesül, hogy tetszőleges n többszörösükre k az f(n)-t is osztja.
HK
|
|
| [561] Hajba Károly | 2004-10-19 15:18:39 |
 110. feladat:
Van egy 101*101-es pontrács. Létezik-e 101 pont úgy, hogy semelyik három nincs egy egyenesen?
HK
|
|
| [560] Suhanc | 2004-10-16 21:07:03 |
 Kedves László!
Köszönöm a segítséget! Elkezdtem megvizsgálni (szigurú értelemben "elkezdtem" , szóval ,mondjuk az első 4 szétbontást;D ), és úgy tűnik, az 1;4 számpár megoldást ad! Eléggé felhősen gondoltam át, szóval könnyen előfordulhat, hogy nem...;D
|
| Előzmény: [559] lorantfy, 2004-10-16 16:35:20 |
|
| [559] lorantfy | 2004-10-16 16:35:20 |
 Kedves Suhanc!
A 102. feladatra gondoltál! Egy kis segítség:
B első megállapításából az derül ki, hogy a szorzat többféleképpen bontható fel két egyjegyű szám szorzatára (továbbiakban szorzatra).
C "Azt én sem" megállapításából pedig az, hogy többféleképpen bontható két egyjegyű szám összegére (továbbiakban összegre).
Abból viszont, hogy mielőtt B nyilatkozott C már tudta, hogy B nem fogja tudni, az derül ki, hogy a C által ismert összeg lehetséges összegre bontásai között nincs olyan amelyik egyféleképpen bontható szorzatra.
Mivel a lehetséges összegek kevesebben vannak (2-20) zárjuk ki először azokat, amelyek összegre bontása egyértelmű.
Majd kizárjuk azokat, melyeknek összegre bontásában van olyan pár, melyek szorzata egyértelműen bontható szorzatra.
Több szám marad, de mivel ezekután B kijelenti: "Akkor már tudom", olyan számot kell keresni a lehetséges szorzatok között, ami csak egy helyen szerepel.
Hát van vele egy kis munka, de ha valaki tud egyszerűbbet, szóljon!
|
| Előzmény: [558] Suhanc, 2004-10-16 14:27:27 |
|
| [558] Suhanc | 2004-10-16 14:27:27 |
 Kedves Mindenki!
Ha valakinek megvan, a 103. feladat megoldása, kérem, írja be, vagy küldje el nekem (suhanc88@freemail.hu)... a számtechtanár napról napra jobban mosolyog... :D
Mivel már elég régóta fenn van, és eddig az édelődés nem volt túl nagy, szerintemolyan is felteheti, aki már ismerte...
|
|
| [557] Hajba Károly | 2004-10-12 22:23:35 |
 Kedves Suhanc!
Sajnos nem jó. Kisértetiesen hasonlít az én első tippemhez, mikor próbáltam megoldani. Én a 11 helyett a 20-at írtam.
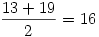 :o( :o(
Egyébként én eddig kétféle megoldását ismerem.
További jó keresgélést minden érdeklődőnek.
HK
|
| Előzmény: [555] Suhanc, 2004-10-12 16:51:08 |
|
| [556] Káli gúla | 2004-10-12 17:07:15 |
 A 104. feladatbeli 2n jegyű számokhoz nem feltétlenül kell programot írni. Egy ilyen, adott hosszú (pl. 100 vagy 2004 jegyű) szám felírása szerintem van olyan érdekes, hogy akár a pontversenyben is ki lehessen tűzni.
|
|
| [555] Suhanc | 2004-10-12 16:51:08 |
 Kedves Onogur!
A szópárbajhoz nem szólnék hozzá (vagytok elegen ;D).
A 109. feladatodra találtam egy lehetséges megoldást!
Az életkorok: 1;2;4;8;11;13;16;17;19. Nyilván csak akkor lesz az átlag egész, ha a kiválsztott két szám paritása megegyezik. Végignézve az eseteket, látható, hogy a feladat feltételeinek megfelelnek.
De vajon van-e másik?:D
|
| Előzmény: [543] Hajba Károly, 2004-10-11 12:00:20 |
|
| [554] Hajba Károly | 2004-10-12 14:34:04 |
 Kedves Edgar!
Csak a vicc kedvéért tippeld meg, de akár bárki más is, hogy javíthatók-e Erich Friedmann feladatai a nem széteső azonos idomok körében itt n= 7, 10, 13 esetében, s ha igen, milyen mértékben? Ezen feladathoz nem kell kemény tárgyi tudás, tudni, hogy mi hol van, csak egy kis kreatív fantázia. Remélem Ti azzal is rendelkeztek. Vagy nem? :o)
Üdv: HK
|
| Előzmény: [552] Edgar, 2004-10-11 21:48:37 |
|
| [553] Hajba Károly | 2004-10-11 22:17:27 |
 Kedves Edgar!
Eredetileg én az n=5-ről nem állítottam, hogy meg lehet oldani. Én azt mondtam, hogy szerintem az n=7 és 13-on lehet javítani. Ezt KL dobta fel, tudjuk viccesen, s ezen már túl is léptünk.
Egyébként, ha megfigyeled, rendszeresen használom a smile-t. S a minap jól jöttél volna a svédek ellen. :o)
Üdv: HK
|
| Előzmény: [552] Edgar, 2004-10-11 21:48:37 |
|
| [552] Edgar | 2004-10-11 21:48:37 |
 Kedves Károly! (...) Ne vedd a szívedre nagyon, egy kis humorérzék talán jobban kezeli a konfliktusokat, mint az, ha megoldatlan problémára invitálod a vitapartert... :) én is tudok 10-20 megoldatlan feladatot, ha szükség lenne rájuk :))
Kedves Dávid! Sajnos nem értek a numerológiához, és szívesen fejleszteném a lényeglátásomat, ezért hadd kérdezzem meg: miben különleges a 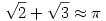 közelítés? közelítés?
Tisztelettel:
Edgar Davids
|
| Előzmény: [551] Hajba Károly, 2004-10-11 20:44:27 |
|
|
|
|
| [548] Csimby | 2004-10-11 19:40:21 |
 Miért? Szerintem ez tök poén! Mindenki keresi az összefüggőt ami valószínű nincs is és akkor itt van a triviális megoldás nem összefüggőre. (nem volt kikötve, hogy legyen összefüggő :-)
|
|
| [547] Hajba Károly | 2004-10-11 19:33:22 |
 Kedves Sambuca!
Hát mit modjak? Anno az én időmben erre azt mondták: Ha nem mondod, hülyén halok meg. :o)
Tudom, hogy tudod, hogy...
Tehát nem ez a feladat. Netalántán az igazi feladatba beletörött a bicskátok? :o)
HK
|
| Előzmény: [544] SAMBUCA, 2004-10-11 17:38:05 |
|
|
| [545] Csimby | 2004-10-11 18:22:32 |
 Nem összefüggőre elég könnyű, itt van 5-re, ez n-re is működik...
|
 |
|














