|
| [581] rizs | 2004-11-19 01:59:16 |
 115. feladat: Van egy börtön, amelynek az udvarán van egy kétállású kapcsoló, véletlenszerű állapotban. A rabok ugyan nem beszélgethetnek, nem adhatnak információt semmilyen módon egymásnak, de bármikor átbillenthetik a kapcsolót a másik állapotába. (A valósággal való egyezés a véletlen műve.) Ebbe a börtönbe visznek N rabot, akik még a rabomobilban összebeszélhetnek. A rabok jól ismerik ennek a börtönnek a szokásait, beeértve a kapcsolót is. Tudják, hogy amikor beviszik őket többet nem beszélhetnek, de "felajánlják" majd nekik, hogy ha mindegyikük már legalább egyszer átállította a kapcsolót és valamelyikük szól, akkor mindegyiküket szabadon engedik. Ha valaki azelőtt szól, hogy valaki még nem nyúlt a kapcsolóhoz, akkor mindenkit kivégeznek. A börtönszokásokhoz tartozik az is, hogy mindenki csak egyedül sétálhat (tehát nem is láthatják a másikat a kapcsolónál) és teljesen véletlenszerű, hogy mikor kit engednek ki sétálni. Semmi garancia nincs arra, hogy mindenki véges időn belül sétálni fog.
Össze tudnak-e beszélni a rabok, hogy szóljon valamelyikük, ha biztosan tudja, hogy mindenki legalább egyszer már hozzányúlt a kapcsolóhoz?
|
|
| [580] rizs | 2004-11-19 01:53:54 |
 még Loríntfy feladta volt annak idején, csak nekem most véletlen kellene a megoldása az 56. feladatnak :) meg lehet tudni? .D:D
illetve még egy remek kis feladat: adjunk meg négy olyan egymást követő prímszámot, amelyek számtani sorozatot alkotnak.
üdv, rizs
|
|
| [579] jenei.attila | 2004-11-18 21:43:23 |
 hasonló módszerrel egyéb érdekes oszthatósági szabályokat lehet találni. Pl. 13|100a+b <=> 13|100a+b-104a-13b 13|-4a-12b <=> 13|a+3b. Itt b már kétjegyű lehet, de b helyett számolhatunk 13-mal való osztási maradékával, vagyis 13|100a+b <=> 13|a+3(b mod 13)
|
| Előzmény: [578] jenei.attila, 2004-11-18 21:17:31 |
|
|
| [577] Hajba Károly | 2004-11-18 19:32:28 |
 A második sor így helyes:
Legyen N=10a+b, akkor minden p-re létezik egy a+j*b kisebb szám, melyik szintén akkor osztható p-vel, mikor N is. Csak a j számot kell ügyesen kitalálni. p=3, j=1; p=13, j=4; p=17, j=5; ...
|
| Előzmény: [576] Hajba Károly, 2004-11-18 19:27:49 |
|
| [576] Hajba Károly | 2004-11-18 19:27:49 |
 Ha valamely p szám 10-zel relatív prím, akkor könnyen készíthető hozzá oszthatósági szabály. Ezek egyikét mutatta be Jenei Attila.
Legyen N=10a+b, akkor minden p-re létezik egy a+j*m kisebb szám, melyik szintén akkor osztható p-vel, mikor N is. Csak a j számot kell ügyesen kitalálni. p=3, j=1; p=13, j=4; p=17, j=5; ...
A p=13-hoz tartozó j=4 a következők szerint adódik, s ez egyben egy kaptafát is ad más oszthatósági szabályok barkácsolásához. Keressük p olyan többszörösét, mely 10 valamely többszörösétől 1 különbséggel adódik. 13, 16, >39<. 4*10 = 3*13 + 1.
N=10a+b
4N-39a=40a-39a+4b
Ha N osztható 13-mal, akkor N=13q
4*13*q-3*13a=a+4b
13(4q-3a)=a+4b
Tehát ekkor a+4b is osztható 13-mal. S ez a első feltételnek megfelelő bármely számra elkészíthető.
HK
|
| Előzmény: [573] zsol, 2004-11-16 17:42:28 |
|
| [575] Csimby | 2004-11-18 17:17:51 |
 Modulo 13, a következő kongruenciák igazak:
100  1, 101 1, 101  10, 102 10, 102  9, 103 9, 103  12, 104 12, 104  3, 105 3, 105  4, 106 4, 106  1, innentől kezdve ismétlődik a kongruencia. Megjegyzed ezt a sorozatot: 1, 10, 9, 12, 3, 4, 1... 1, innentől kezdve ismétlődik a kongruencia. Megjegyzed ezt a sorozatot: 1, 10, 9, 12, 3, 4, 1...
Egy n szám akkor osztható 13-mal, ha a számjegyeiből alkotott kifejezés:
a0+10a1+9a2+12a3+3a4+4a5+a6+10a7+...
osztható 13-mal. Nem mondom, hogy érdemes használni...
|
| Előzmény: [573] zsol, 2004-11-16 17:42:28 |
|
| [574] jenei.attila | 2004-11-18 14:01:47 |
 Szóval: a 13-mal való egyik oszthatósági szabály:
A 10a+b alakú szám pontosan akkor osztható 13-mal, ha a+4b is osztható 13-mal.
A nehezebb rész annak belátása, hogy ha 13|10a+b, akkor 13|a+4. Legyen 10a+b=13n. Ekkor 10|13n-b => 10|39n-3b => (40n-et kivonva)10|n+3b. Legyen ezután k=(n+3b)/10, vagyis n=10k-3b. Ezért 10a+b=13n=130k-39b => 10a+40b=130k => a+4b=13k, vagyis 13|a+4b.
A másik irány bizonyítása könnyebb, az utolsó mondatot kell csak visszafelé értelmezni.
|
| Előzmény: [573] zsol, 2004-11-16 17:42:28 |
|
| [573] zsol | 2004-11-16 17:42:28 |
 Sziasztok , A feladat a következő, mely számok oszthatók 13mal? Mi erre az oszthatósági szabály ?
|
|
| [572] Maga Péter | 2004-11-16 08:49:35 |
 Kedves Attila!
A megoldásod jó. Lényegében én is így csináltam (mármint testbővítéssel).
A megoldásban felhasznált másodfokú testbővítés egyébként is nagyon szép, Surányi László: Algebra-ját ajánlom mindenkinek, akit érdekel a dolog!
|
| Előzmény: [571] jenei.attila, 2004-11-15 23:33:36 |
|
| [571] jenei.attila | 2004-11-15 23:33:36 |
 Válasz Maga Péter feladatára: A nem eleme jelet  helyettesíti, mivel nem találtam megfelelőbbet. helyettesíti, mivel nem találtam megfelelőbbet.
Bizonyítsuk be, hogy minden n 2 természetes számra 2 természetes számra
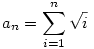
irracionális.
Megoldás:
Tekintsük testek következő, tartalmazásra nézve szigorúan növekvő sorozatát:
Q1 Q2 Q2 Q3 Q3 Q5 Q5 ... ... Qpk Qpk
, ahol Q1 a racionális számok teste, Q2 a Q1  -vel való bővítése, Qpj pedig a Qpj-1 bővítése -vel való bővítése, Qpj pedig a Qpj-1 bővítése 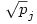 -vel (p1,p2,...,pk az első egymás utáni prímek). Bebizonyítjuk, hogy aj -vel (p1,p2,...,pk az első egymás utáni prímek). Bebizonyítjuk, hogy aj Qpl, de aj Qpl, de aj Qpl-1 valamely l-re (j Qpl-1 valamely l-re (j 1 és l 1 és l 1), amiből következik, hogy an irracionális (n 1), amiből következik, hogy an irracionális (n 2). A sorozat egy testét csak prím négyzetgyökével érdemes bővíteni, mert ha x nem prím, akkor kisebb prímek szorzatára bomlik, amelyek négyzetgyökével már bővítettünk. Prím négyzetgyökével való bővítés pedig valóban bővebb testet eredményez. Ennek bizonyítása teljes indukcióval lehetséges. Mivel 2). A sorozat egy testét csak prím négyzetgyökével érdemes bővíteni, mert ha x nem prím, akkor kisebb prímek szorzatára bomlik, amelyek négyzetgyökével már bővítettünk. Prím négyzetgyökével való bővítés pedig valóban bővebb testet eredményez. Ennek bizonyítása teljes indukcióval lehetséges. Mivel
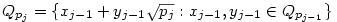
(egyszerű bizonyítani), ezért bármely z racionális szám négyzetgyöke 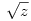 pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j 2), ha 2), ha 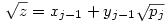 valamely xj-1,yj-1 valamely xj-1,yj-1 Qpj-1. Nyilvánvaló, hogy yj-1 Qpj-1. Nyilvánvaló, hogy yj-1 0, de ha ugyanekkor xj-1 0, de ha ugyanekkor xj-1 0 is teljesülne, akkor négyzetre emelve és átrendezve azt kapnánk, hogy 0 is teljesülne, akkor négyzetre emelve és átrendezve azt kapnánk, hogy 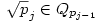 lenne az indukciós feltevéssel ellentétben. Tehát lenne az indukciós feltevéssel ellentétben. Tehát 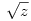 (z racionális) pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j (z racionális) pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j 2), ha létezik yj-1 2), ha létezik yj-1 Qpj-1, amire Qpj-1, amire 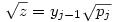 , vagyis , vagyis 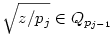 . Másképp fogalmazva: . Másképp fogalmazva: 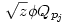 akkor és csak akkor, ha akkor és csak akkor, ha 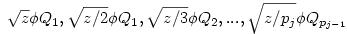 . Ugyanezt a feltételt alkalmazva a feltételben szereplő racionális számok négyzetgyökeire is, azt kapjuk hogy, . Ugyanezt a feltételt alkalmazva a feltételben szereplő racionális számok négyzetgyökeire is, azt kapjuk hogy, 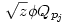 akkor és csak akkor, ha akkor és csak akkor, ha 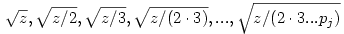 irracionális (ahol a négyzetgyökök nevezőiben a 2-től pj-ig terjedő prímek minden lehetséges szorzata szerepel). Könnyű bebizonyítani, hogy a fenti alakú négyzetgyökök irracionálisak, ha z prím (két négyzetmentes természetes szám hányadosának négyzetgyöke irracionális). Vagyis irracionális (ahol a négyzetgyökök nevezőiben a 2-től pj-ig terjedő prímek minden lehetséges szorzata szerepel). Könnyű bebizonyítani, hogy a fenti alakú négyzetgyökök irracionálisak, ha z prím (két négyzetmentes természetes szám hányadosának négyzetgyöke irracionális). Vagyis 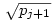 valóban bővíti a Qpj testet. valóban bővíti a Qpj testet.
Vissztérve az eredeti feladatra: azt kell bebizonyítani, hogy ha an Qpj volt (de an Qpj volt (de an Qpj-1), akkor an-hez Qpj-1), akkor an-hez 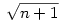 -et hozzáadva an+1 -et hozzáadva an+1 Qpj vagy an+1 Qpj vagy an+1 Qpj+1 lesz, de nem lehet hogy an+1 Qpj+1 lesz, de nem lehet hogy an+1 Qpj-1 és an+1 Qpj-1 és an+1 Qpjlesz. Vagyis an-hez Qpjlesz. Vagyis an-hez 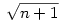 hozzáadásával az adott testben maradunk, vagy eggyel feljebb lépünk, de nem lépünk alacsonyabb indexű testbe. Ha hozzáadásával az adott testben maradunk, vagy eggyel feljebb lépünk, de nem lépünk alacsonyabb indexű testbe. Ha  , vagy , vagy 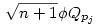 ( ( 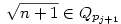 ), akkor nyilván igaz, hogy nem lépünk alacsonyabb indexű testbe. Ha ), akkor nyilván igaz, hogy nem lépünk alacsonyabb indexű testbe. Ha 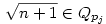 , akkor mint már láttuk, , akkor mint már láttuk, 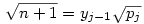 (yj-1 (yj-1 Qpj-1 és yj-1>0) és an hasonló felírásában a Qpj-1 és yj-1>0) és an hasonló felírásában a 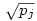 együtthatója szintén pozitív. Ezért ebben az esetben sem lépünk vissza az alacsonyabb indexű testbe. együtthatója szintén pozitív. Ezért ebben az esetben sem lépünk vissza az alacsonyabb indexű testbe.
|
| Előzmény: [523] Maga Péter, 2004-10-09 22:04:22 |
|
|
| [569] matekos04 | 2004-11-09 17:52:26 |
 113 feladat. Udv. mindenkinek!
A feladatom igy szol:
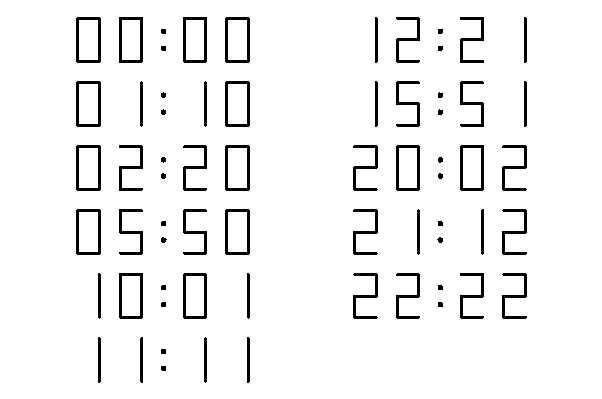
Tegyuk fel hogy van egy digitalis orank. Hany olyan idopont van egy nap alatt (24 h),hogy ha fejtetore allitjuk az orat ugyanazt a szamot kapjuk meg?
|
 |
|
| [568] Maga Péter | 2004-10-28 09:39:55 |
 112. feladat (a 108. feladat folytatása):
Határozzuk meg minden n>1-re azokat az a1,a2,...,an n-eseket, ahol minden ai 0 vagy 1, és
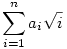 racionális! racionális!
|
|
| [567] Sirpi | 2004-10-22 10:34:40 |
 Megkerestem az ominózus cikket. Úgy tűnik, egyszerűen lemaradt az egyik nyitó zárójel. Az állítás azt mondja ki, hogy minden h>0-hoz van olyan N, hogy minden n>N-re el lehet helyezni legalább 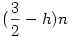 pontot a megadott tulajdonsággal. pontot a megadott tulajdonsággal.
|
| Előzmény: [566] Hajba Károly, 2004-10-22 10:02:38 |
|
| [566] Hajba Károly | 2004-10-22 10:02:38 |
 Megtaláltam a jelzett megoldást a Kömal archivumban 1998/2 66-67. o.
A megj/4. pontban szereplő (3/2)-h)n képlet, mely feltehetőleg nyomdaszedési hiba, értelmezhetetlen. Mi lehet a helyes képlet?
HK
|
| Előzmény: [565] Kemény Legény, 2004-10-21 23:34:45 |
|
|
|
| [563] Hajba Károly | 2004-10-19 15:22:00 |
 Az előző két feladatot egy hálón fellelt gyűjteményből emeltem át. Eredetüket a "közreadója" sem ismeri (Pósa, régi Kömal, ...? :o)
HK
|
|
| [562] Hajba Károly | 2004-10-19 15:19:35 |
 111. feladat:
Tetszőleges n pozitív egészre jelölje f(n) az n szám fordítottját tízes számrendszerben. (Például f(1994)=4991, f(5200)=25.) Keressük meg azokat a pozitív egész k számokat, amelyekre teljesül, hogy tetszőleges n többszörösükre k az f(n)-t is osztja.
HK
|
|
| [561] Hajba Károly | 2004-10-19 15:18:39 |
 110. feladat:
Van egy 101*101-es pontrács. Létezik-e 101 pont úgy, hogy semelyik három nincs egy egyenesen?
HK
|
|
| [560] Suhanc | 2004-10-16 21:07:03 |
 Kedves László!
Köszönöm a segítséget! Elkezdtem megvizsgálni (szigurú értelemben "elkezdtem" , szóval ,mondjuk az első 4 szétbontást;D ), és úgy tűnik, az 1;4 számpár megoldást ad! Eléggé felhősen gondoltam át, szóval könnyen előfordulhat, hogy nem...;D
|
| Előzmény: [559] lorantfy, 2004-10-16 16:35:20 |
|
| [559] lorantfy | 2004-10-16 16:35:20 |
 Kedves Suhanc!
A 102. feladatra gondoltál! Egy kis segítség:
B első megállapításából az derül ki, hogy a szorzat többféleképpen bontható fel két egyjegyű szám szorzatára (továbbiakban szorzatra).
C "Azt én sem" megállapításából pedig az, hogy többféleképpen bontható két egyjegyű szám összegére (továbbiakban összegre).
Abból viszont, hogy mielőtt B nyilatkozott C már tudta, hogy B nem fogja tudni, az derül ki, hogy a C által ismert összeg lehetséges összegre bontásai között nincs olyan amelyik egyféleképpen bontható szorzatra.
Mivel a lehetséges összegek kevesebben vannak (2-20) zárjuk ki először azokat, amelyek összegre bontása egyértelmű.
Majd kizárjuk azokat, melyeknek összegre bontásában van olyan pár, melyek szorzata egyértelműen bontható szorzatra.
Több szám marad, de mivel ezekután B kijelenti: "Akkor már tudom", olyan számot kell keresni a lehetséges szorzatok között, ami csak egy helyen szerepel.
Hát van vele egy kis munka, de ha valaki tud egyszerűbbet, szóljon!
|
| Előzmény: [558] Suhanc, 2004-10-16 14:27:27 |
|
| [558] Suhanc | 2004-10-16 14:27:27 |
 Kedves Mindenki!
Ha valakinek megvan, a 103. feladat megoldása, kérem, írja be, vagy küldje el nekem (suhanc88@freemail.hu)... a számtechtanár napról napra jobban mosolyog... :D
Mivel már elég régóta fenn van, és eddig az édelődés nem volt túl nagy, szerintemolyan is felteheti, aki már ismerte...
|
|






 1, 101
1, 101 
 helyettesíti, mivel nem találtam megfelelőbbet.
helyettesíti, mivel nem találtam megfelelőbbet.  2 természetes számra
2 természetes számra  Q2
Q2 Qpl, de aj
Qpl, de aj 1 és l
1 és l