| [638] Csimby | 2004-12-07 22:07:15 |
 Ha valakit érdekel, a "Bizonyítások a Könyből" című könyvben (Könyvajánló [27] és [28]) például 3 bizonyítást is adnak erre :
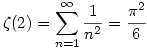
Ebből:
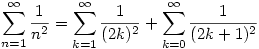
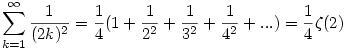
Tehát:
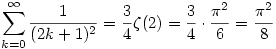
Megjegyzés:
A Riemann-féle  (s) zéta függvényt s>1-re (s) zéta függvényt s>1-re 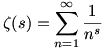 -ként definiáljuk. -ként definiáljuk.
|
| Előzmény: [636] Lóczi Lajos, 2004-12-03 17:44:57 |
|
|
|
| [634] lorantfy | 2004-12-02 13:47:46 |
 Kedves Csimbi!
Kösz a gyors megoldást! Aki nem ismerte, tanulhat belőle!
Csak a beírás formájával van gondom.
Meg kellett volna törni a sort mert így megszélesíti a lapot és nem lehet "átlátni" a hozzászólásokat.
Elég gyér a Fórum látogatottsága a héten. Aki ráér tegyen ellene!
|
| Előzmény: [646] Csimby, 2004-12-02 12:56:46 |
|
|
| [633] lorantfy | 2004-12-02 11:34:29 |
 Lóczi Lajos [631]-beli feladata a 122.,[632]-beli pedig a 123.
124. feladat: Bizonyítsuk be, hogy minden n természetes számra:
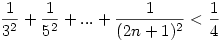
|
|
| [632] SchZol | 2004-11-26 12:17:38 |
 Kedves László!
A Bolzano-Weierstrass tétel valóban az, amit Géza írt, viszont tényleg van egy olyan Bolzano tétel is, ami azt mondja ki, hogy:
Ha f folytonos [a, b]-ben és f(a)<c<f(b), akkor létezik   (a,b): f( (a,b): f( )=c )=c
Üdv, Zoli
|
| Előzmény: [629] lorantfy, 2004-11-25 22:22:24 |
|
| [631] Lóczi Lajos | 2004-11-26 01:04:46 |
 Keressük meg azokat a pozitív x,y,z számokat, melyekre teljesül az xy=z, yz=x és zx=y egyenletrendszer.
|
|
| [630] Lóczi Lajos | 2004-11-26 00:52:44 |
 Ennek mintájára:
Adjunk példát olyan, az egész számegyenesen értelmezett f valós függvényre, amelyre f(f(x))=-x.
Vizsgáljuk meg az analóg problémát hármas vagy magasabb kompozícióra. Még régebben keresgéltem ilyen függvényeket, ebből nálam szép, forgásszimmetrikusnak kinéző ábrák születtek...
|
| Előzmény: [622] jenei.attila, 2004-11-24 20:39:06 |
|
| [629] lorantfy | 2004-11-25 22:22:24 |
 Kedves Géza!
Igazad van! A Bolzano-Weierstrass a számsorozatoknál, az említett tétel. Ennek ellenére több helyen is olvastam már, hogy zárt intervallumon folytonos fgv... témában Bolzano-Weierstass tételre hivatkoztak - eszerint helytelenül.
|
| Előzmény: [628] Kós Géza, 2004-11-25 14:18:45 |
|
|
|
| [626] jenei.attila | 2004-11-25 10:01:11 |
 Én is így oldottam meg, figyelembe véve Géza kiegészítését. A szürjektivitásról szóló indoklást nem értem, hiszen egy függvényről akkor állítható hogy szürjektív, ha megadjuk az értékkészletét. Inkább csak annyi kell, hogy g értelmezési tartománya és értékéészlete megegyezik, ezért értelmezhető gg. Folytonos és injektív függvény pedig szigorúan monoton (folytonos fv. bármely két értéke közötti minden étéket felvesz. Mi a tétel neve?).
Egyébként a feladat a nyári kisinóci táborban volt feladva (legalábbis én ott találkoztam vele először). Esetleg megbeszélhetnénk a többi feladatot is.
|
| Előzmény: [623] HOMI, 2004-11-25 02:24:03 |
|
|
|
| [623] HOMI | 2004-11-25 02:24:03 |
 A g(x) injektiv,mert ha g(a)=g(b) akkor 1/a=g(g(a))=g(g(b))=1/b,azaz a=b.Az 1/x mindent felvesz (0,+végtelen)-en,igy g(g(x)) szürjektiv,azaz g(x) is szürjektiv.A g(x) folytonos,injektiv,szürjektiv tehát szigorúan monoton.Ha g(x) szig.mon.növekedne,g(g(x)) is azt tenné de 1/x szig.mon csökken.Igy g szig mon csökken és a felvett értékkészlete a teljes(0,+végtelen).Ekkor ha x 'kicsi', g(x) 'nagy',g(g(x)) 'kicsi' ,de 1/x 'nagy'.Ez ellentmondás,mert g(g(x)))=1/x.(A fentiek pontos megfogalmazása: ha x tart 0-hoz g(x)->+végtelen,igy g(g(x))->0,de 1/x->végtelen).
|
| Előzmény: [622] jenei.attila, 2004-11-24 20:39:06 |
|
| [622] jenei.attila | 2004-11-24 20:39:06 |
 Egy nem túl nehéz, de szerintem érdekes feladat:
Bizonyítsuk be, hogy nincs olyan g:R+ R+ folytonos függvény, amelyre g(g(x))=1/x minden x R+ folytonos függvény, amelyre g(g(x))=1/x minden x R+-ra. R+-ra.
|
|
|
| [620] rizs | 2004-11-24 19:14:02 |
 Ha már Fibonacci a téma, akkor ezt ajánlom még egyszer :) 118.: Ha a Fibonacci sorozat elemeit egy-egy tizedeshellyel eltolva (akár balról jobbra, akár jobbról balra haladva) egymás alá írjuk és összeadjuk, akkor a sok szám összege végül ismétlődő szakaszokból fog állni, tehát olyan lesz, mint a végtelen szakaszos tizedestörtek. Sőt, nem csak olyan, hanem az is! Ha megfelelő helyre tesszük a tizedesvesszőt, akkor a két összeg éppen 1/A, illetve 1/B értékű lesz, ahol A és B prímszámok. Mennyi A és B?
|
|
| [619] Maga Péter | 2004-11-24 18:45:38 |
 A hatványsoros megoldáshoz hozzátenném, hogy az összes ilyen tulajdonságú függvényt generálja. Tehát: az ex hatványsorából érdemes indulni, ez 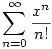 . Ezek után pedig a minden 0 és 7 közötti egész i-re a 8k+i alakú egészekhez tartozó együtthatókat ugyanazzal a ci konstanssal szorozni. A tagok elhagyása (amit szefoharcos írt) a ci=0. Csak arra kell figyelni, hogy ha ügyetlenül választjuk meg ezeket a konstansokat, akkor korábbi derivált is lehet az eredeti függvény. Ez akkor teljesül, ha ugyanazt a kostans szorzót (ci) választjuk olyan együtthatókhoz, amelyeknek különbsége 8-nál kisebb, a 8-hoz nem relatív prím. A felírt hatványsor mindig értelmes, ezt a Cauchy-Hadamaard kritériummal lehet ellenőrizni. . Ezek után pedig a minden 0 és 7 közötti egész i-re a 8k+i alakú egészekhez tartozó együtthatókat ugyanazzal a ci konstanssal szorozni. A tagok elhagyása (amit szefoharcos írt) a ci=0. Csak arra kell figyelni, hogy ha ügyetlenül választjuk meg ezeket a konstansokat, akkor korábbi derivált is lehet az eredeti függvény. Ez akkor teljesül, ha ugyanazt a kostans szorzót (ci) választjuk olyan együtthatókhoz, amelyeknek különbsége 8-nál kisebb, a 8-hoz nem relatív prím. A felírt hatványsor mindig értelmes, ezt a Cauchy-Hadamaard kritériummal lehet ellenőrizni.
|
| Előzmény: [618] Lóczi Lajos, 2004-11-24 18:20:46 |
|
| [618] Lóczi Lajos | 2004-11-24 18:20:46 |
 Valóban, amely Általad említett függvény a koszinusz-analógiával is felírható persze:
legyen ismét  egy primitív nyolcadik egységgyök, ekkor egy primitív nyolcadik egységgyök, ekkor
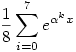
lesz az a valós függvény, amely ex hatványsorából úgy keletkezik, hogy csak minden 8. tagot hagyunk meg, azaz a fenti függvény 0 körüli hatványsorának eleje
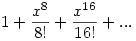
Egyébként ez csak valós elemi függvényekkel kifejezve egy harmadik alakban így fest:
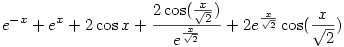
vagy, ha a ch koszinusz-hiperbolikusz függvényt is használhatom, akár így:
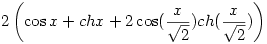
|
| Előzmény: [617] szefoharcos, 2004-11-24 17:43:32 |
|
| [617] szefoharcos | 2004-11-24 17:43:32 |
 Kedves Lajos!
Gratulaalok a megoldaasaidhoz! A Fibonacci-szaamokra ugyanezt talaaltam een is, de a fuggveenyesre volna egy megjegyzeesem, ami nem toolem szaarmazik: hatvaanysorok... Ahogy Kemeeny Legeeny is megoldotta, mieloott hangneme miatt letiltottaak volna: Az xn/n! sor minden 8. tagjaat hagyjuk csak meg. Konnyuu ellenoorizni, hogy ez joo.
|
|
| [616] Lóczi Lajos | 2004-11-24 15:03:36 |
 Egy kis segítség a 121. feladathoz:
némi keresgélés után rájöttem, hogy
F2n+1=Fn+12+Fn2 illetve
F2n=Fn+12-Fn-12,
ahol n pozitív természetes szám és Fn az n-edik Fibonacci szám, ha a sorozat így kezdődik: F1=1, F2=1, F3=2, stb.
Ezeket már könnyű bizonyítani például a Fibonacci-számok explicit alakjából.
|
| Előzmény: [604] szefoharcos, 2004-11-23 22:42:38 |
|
|
| [614] Lóczi Lajos | 2004-11-24 12:54:56 |
 Nyilván nem, csak ez az egy ilyen hármasiker van. Hiszen ha az első tag 3-nál nagyobb prím, akkor 3-mal maradékosan osztva 1-et vagy 2-t ad. De ekkor az első esetben a sorozat 2. tagja 3-mal osztható lenne, míg a második esetben a sorozat 3. tagja volna 3-mal osztható.
|
| Előzmény: [612] Hajba Károly, 2004-11-24 12:48:27 |
|



 (s) zéta függvényt s>1-re
(s) zéta függvényt s>1-re 



 (a,b): f(
(a,b): f(

 R+ folytonos függvény, amelyre g(g(x))=1/x minden x
R+ folytonos függvény, amelyre g(g(x))=1/x minden x

 egy primitív nyolcadik egységgyök, ekkor
egy primitív nyolcadik egységgyök, ekkor 