|
|
|
| [648] Csimby | 2004-12-16 22:01:15 |
 129.feladat
Keressünk összefüggést a Pascal háromszög és a Fibonacci sorozat között.
|
|
| [647] Csimby | 2004-12-16 21:44:11 |
 128. feladat
Egy 8×8-as sakktáblán 8 bástyát helyeztünk el úgy, hogy semelyik kettő sem üti egymást. Bizonyítsuk be, hogy páros sok bástya áll fekete mezőn. (Arany Dani döntő volt, a KöMaL-ban szerepel, de nem mindenkinek jár az újság)
|
|
|
| [644] Szabó Dániel | 2004-12-10 20:02:27 |
 Matekszakkörön találkoztam a következő feladattal: hány olyan 1000000-nál kisebb természetes szám van, melynek a számjegyeinek összege páros, s a nála eggyel nagyobb szám számjegyeinek összege is páros. Leszámoltam Turbo Pascallal, az eredmény 45455. Tanárom szerint 45454. Melyikünknek van igaza?
|
|
|
| [642] Kemény Legény | 2004-12-08 20:43:54 |
 Ha valamelyik ismeretlen 1,akkor a többi is az,és ez megoldás. A 3 egyenlet logaritmusát összeszorozva kapjuk,hogy : xyzlog(x)log(y)log(z)=log(x)log(y)log(z),mivel egyik sem 1(ezt már feltehetjük) xyz=1.Ha nem mind 1: vagy van 2 db 1-nél kisebb vagy lesz 2 db 1-nél nagyobb.Ha pl x és y 1-nél nagyobb: z=x**y>1,azaz xyz>1*1*1=1,nem lehetséges.Ha x és y 1-nél kisebbek z=x**y<1 azaz xyz<1*1*1=1 nem lehetséges.Igy x=y=z=1 a megoldás. (A ** jelöli a hatványozást).
|
| Előzmény: [631] Lóczi Lajos, 2004-11-26 01:04:46 |
|
| [641] Csimby | 2004-12-08 18:39:12 |
 A bal alsó sarokban szereplő számjegy a feltételek miatt nem szerepelhet megegyszer a szürkével jelölt négyzeteken. A skatulya-elv miatt rögtön látszik, hogy mindegyik számjegy pontosan 6-szor kell, hogy előforduljon. Tehát a fennmaradt fehér mezőkön összesen 5-ször kell elhelyezni azt a számjegyet ami a bal alsó sarokban szerepel. Ekkor a két egybevágó fehér rész közül az egyikben 3-szor kell, hogy szerepeljen ez a számjegy. Ez pedig már könnyen látszik, hogy nem lehetséges...
|
 |
| Előzmény: [639] rizs, 2004-12-08 14:28:16 |
|
| [640] rizs | 2004-12-08 14:29:44 |
 Van egy számológépünk, ami kicsit komolyabb, mint egy négyműveletes, tehát tud olyan műveleteket (az inverzeikkel együtt!), hogy gombnyomásra négyzet- és köbgyököt von, van rajta sinus, cosinus, tangens (mindezek hiperbolikus változatai is), 1/x, 10 és e alapú logaritmus, faktoriális. Egy cetlire fel van írva két különböző pozitív egész szám (többjegyű is lehet). Az elsőt még be tudjuk pötyögni a cetliről, de azután már az összes számjegy gombja (0-9) és a tizedesvessző, valamint a négy alapművelet gombja is elromlottnak tekintendő, még az = sem működik. Ezekhez nem szabad nyúlni. A feladat az, hogy csak a rendelkezésre álló matematikai funkciók gombjainak használatával elérjük, hogy a beírt szám helyett előbb-utóbb a cetlin lévő másik pozitív egész szám legyen a kijelzőn. Tehát olyan eljárást kell keresni, amelynek kiindulása az egyik pozitív egész szám, végeredménye pedig a másik, azok értékétől és különbségétől függetlenül. (A kiindulási szám akármennyivel kisebb, de nagyobb is lehet a másiknál.) A módszernek tehát olyannak kell lennie, hogy bármely két pozitív egész számra működjön.
|
|
| [639] rizs | 2004-12-08 14:28:16 |
 sziasztok!
szerintetek lehet rajzolni olyan 6*6-os bűvös négyzetet, amelynek mindegyik sorában, oszlopában és átlójában (átlóként értelmezünk minden átlót, tehát a sarok elemeket, az azok mellett elhelyezkedő 2 elemű átlót, stb.) az 1, 2, 3, 4, 5, 6 számok midegyike legfeljebb 1 alkalommal fordul elő. Természetesen ez azt jelenti, hogy a sorokban, az oszlopokban, és a főátlókban mindegyik szám pontosan egyszer szerepel.
|
|
| [638] Csimby | 2004-12-07 22:07:15 |
 Ha valakit érdekel, a "Bizonyítások a Könyből" című könyvben (Könyvajánló [27] és [28]) például 3 bizonyítást is adnak erre :
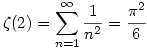
Ebből:
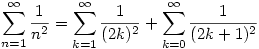
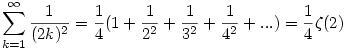
Tehát:
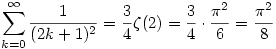
Megjegyzés:
A Riemann-féle  (s) zéta függvényt s>1-re (s) zéta függvényt s>1-re 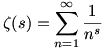 -ként definiáljuk. -ként definiáljuk.
|
| Előzmény: [636] Lóczi Lajos, 2004-12-03 17:44:57 |
|
|
|
| [634] lorantfy | 2004-12-02 13:47:46 |
 Kedves Csimbi!
Kösz a gyors megoldást! Aki nem ismerte, tanulhat belőle!
Csak a beírás formájával van gondom.
Meg kellett volna törni a sort mert így megszélesíti a lapot és nem lehet "átlátni" a hozzászólásokat.
Elég gyér a Fórum látogatottsága a héten. Aki ráér tegyen ellene!
|
| Előzmény: [646] Csimby, 2004-12-02 12:56:46 |
|
|
| [633] lorantfy | 2004-12-02 11:34:29 |
 Lóczi Lajos [631]-beli feladata a 122.,[632]-beli pedig a 123.
124. feladat: Bizonyítsuk be, hogy minden n természetes számra:
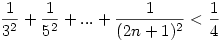
|
|
| [632] SchZol | 2004-11-26 12:17:38 |
 Kedves László!
A Bolzano-Weierstrass tétel valóban az, amit Géza írt, viszont tényleg van egy olyan Bolzano tétel is, ami azt mondja ki, hogy:
Ha f folytonos [a, b]-ben és f(a)<c<f(b), akkor létezik   (a,b): f( (a,b): f( )=c )=c
Üdv, Zoli
|
| Előzmény: [629] lorantfy, 2004-11-25 22:22:24 |
|
| [631] Lóczi Lajos | 2004-11-26 01:04:46 |
 Keressük meg azokat a pozitív x,y,z számokat, melyekre teljesül az xy=z, yz=x és zx=y egyenletrendszer.
|
|
| [630] Lóczi Lajos | 2004-11-26 00:52:44 |
 Ennek mintájára:
Adjunk példát olyan, az egész számegyenesen értelmezett f valós függvényre, amelyre f(f(x))=-x.
Vizsgáljuk meg az analóg problémát hármas vagy magasabb kompozícióra. Még régebben keresgéltem ilyen függvényeket, ebből nálam szép, forgásszimmetrikusnak kinéző ábrák születtek...
|
| Előzmény: [622] jenei.attila, 2004-11-24 20:39:06 |
|
| [629] lorantfy | 2004-11-25 22:22:24 |
 Kedves Géza!
Igazad van! A Bolzano-Weierstrass a számsorozatoknál, az említett tétel. Ennek ellenére több helyen is olvastam már, hogy zárt intervallumon folytonos fgv... témában Bolzano-Weierstass tételre hivatkoztak - eszerint helytelenül.
|
| Előzmény: [628] Kós Géza, 2004-11-25 14:18:45 |
|
|
|
| [626] jenei.attila | 2004-11-25 10:01:11 |
 Én is így oldottam meg, figyelembe véve Géza kiegészítését. A szürjektivitásról szóló indoklást nem értem, hiszen egy függvényről akkor állítható hogy szürjektív, ha megadjuk az értékkészletét. Inkább csak annyi kell, hogy g értelmezési tartománya és értékéészlete megegyezik, ezért értelmezhető gg. Folytonos és injektív függvény pedig szigorúan monoton (folytonos fv. bármely két értéke közötti minden étéket felvesz. Mi a tétel neve?).
Egyébként a feladat a nyári kisinóci táborban volt feladva (legalábbis én ott találkoztam vele először). Esetleg megbeszélhetnénk a többi feladatot is.
|
| Előzmény: [623] HOMI, 2004-11-25 02:24:03 |
|






 (s) zéta függvényt s>1-re
(s) zéta függvényt s>1-re 


 (a,b): f(
(a,b): f(