| [664] SchZol | 2004-12-28 23:44:15 |
 Hello PolarFox!
Alkalmazzuk a számtani és mértani közép közötti egyenlőtlenséget, mivel pozitív tagokról van szó ezt megtehetjük. A tagok amire alkalmazzuk x3, 2y3, 4z3.
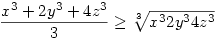
átrendezve:
x3+2y3+4z3-6xyz 0 egyenlőség akkor lép fel, ha a tagok amire alkalmaztuk a közepeket egyenlőek, vagyis x3=2y3=4z3 Ehhez pedig az kell, hogy a tagokban a 2-es azonos kitevőn legyen, vagyis, ha x-ben a-val, y-ben b vel, z-ben c-vel jelöljük a kettőnek a kitevőjét, akkor az alábbi egyenletnek igaznak kell lenni: 3a=3b+1=3c+2 ahol a,b,c egészek. Ez viszont nem lehet soha egyenlő, mert 3-mal osztva különbőző maradékot adnak. Ebből viszont az következik, hogy az egyetlen megoldás a triviális megoldás, ha a x,y,z is 0. 0 egyenlőség akkor lép fel, ha a tagok amire alkalmaztuk a közepeket egyenlőek, vagyis x3=2y3=4z3 Ehhez pedig az kell, hogy a tagokban a 2-es azonos kitevőn legyen, vagyis, ha x-ben a-val, y-ben b vel, z-ben c-vel jelöljük a kettőnek a kitevőjét, akkor az alábbi egyenletnek igaznak kell lenni: 3a=3b+1=3c+2 ahol a,b,c egészek. Ez viszont nem lehet soha egyenlő, mert 3-mal osztva különbőző maradékot adnak. Ebből viszont az következik, hogy az egyetlen megoldás a triviális megoldás, ha a x,y,z is 0.
Remélem jó és érthető!
Üdv, Zoli
|
| Előzmény: [663] PolarFox, 2004-12-28 19:47:08 |
|
| [663] PolarFox | 2004-12-28 19:47:08 |
 Sziasztok. Nagy problémám van, már rég óta agyalok egy egyenleten de nem sikerül szorzattá alakítanom, légyszi segítsetek. A feladat: (nem tudok felső indexet írni) x*x*x+2*y*y*y+4*z*z*z-6xyz=0 tehát x3+2y3+4z3-6xyz=0 oldd meg az egyenletet, ha x;y;z eleme a pozitív egész számoknak.
|
|
| [662] zitoca | 2004-12-27 10:58:10 |
 Székely J. Gábor Paradoxonok a véletlen matematikájában c könyvében azt olvastam, hogy 100 lottószelvényt kell kitöltenünk ahhoz, hogy biztos legyen kettes találatunk az ötöslottón (ennyi minimum kell és ennyi elég is), viszont nem tudjuk megmondani, hogy hány szelvény kell minimum a biztos hármas illetve négyes találat eléréséhez.
Tudna valaki ennek a problémának a mélységéről, kutatási irányáról részletesebben írni? Nagyon érdekesnek találom a problémát, mert egyszerű a kérdés, bárkinek eszébe juthat és mégsem tudjuk megválaszolni...sőt ezek szerint a meggondolások messzebbre is vezetnek, mint ahogy elsőre tűnik.
|
|
| [661] jonas | 2004-12-23 23:10:27 |
 Szoval a Pascal-haromszogben a paratlan szamok egy Sierpinski-haromszog nevu fraktalon helyezkednek el, es erdekes modon ezt a Sierpinski-haromszoget egy vonallal le lehet rajzolni:
|
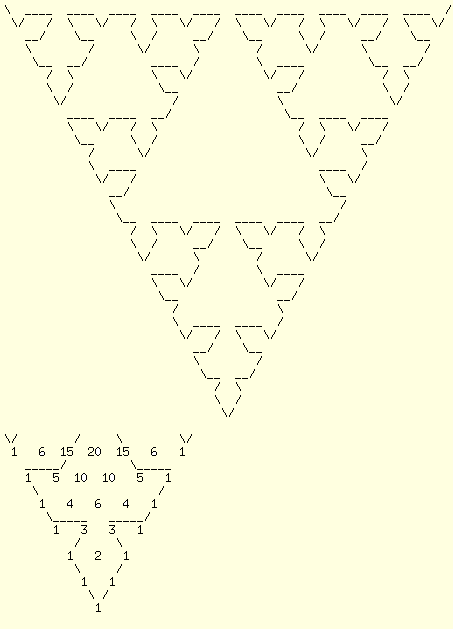 |
| Előzmény: [659] Lóczi Lajos, 2004-12-23 12:25:17 |
|
|
| [659] Lóczi Lajos | 2004-12-23 12:25:17 |
 Megértettem, de szerintem pont fordítva van, mint ahogyan írtad:
Legyen pl. m=2, n=1, ekkor 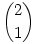 páros, az 1 és 2 számok kettes számrendszerben 01 és 10, ezek bitenkénti AND NOT-ja kettes számrendszerben 01, azaz nem nulla. páros, az 1 és 2 számok kettes számrendszerben 01 és 10, ezek bitenkénti AND NOT-ja kettes számrendszerben 01, azaz nem nulla.
Legyen most m=3, n=1, ekkor 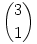 páratlan, az 1 és 3 számok kettes számrendszerben 01 és 11, melyek bitenkénti AND NOT-ja kettes számrendszerben 00, azaz nulla. páratlan, az 1 és 3 számok kettes számrendszerben 01 és 11, melyek bitenkénti AND NOT-ja kettes számrendszerben 00, azaz nulla.
Tehát 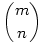 pontosan akkor páratlan, ha (a fenti átírás szerint, balról a megfelelő számú nullákkal kiegészítve) n BIT AND (NOT m) minden bináris jegye 0. pontosan akkor páratlan, ha (a fenti átírás szerint, balról a megfelelő számú nullákkal kiegészítve) n BIT AND (NOT m) minden bináris jegye 0.
Az idézett honlapon viszont nem egyértelmű a kiszámítási utasítás, tehát nem mondhatjuk rá, hogy rossz: ott csak annyi van írva, hogy n XOR m kifejezésből lehet KISZÁMOLNI (de hogy hogyan, az kérdés).
|
| Előzmény: [656] jonas, 2004-12-21 20:51:57 |
|
| [658] Sirpi | 2004-12-23 12:10:57 |
 Igaz, igaz, kicsit figyelmetlen voltam.
n=2-es számrendszerben mondjuk kicsit furcsa a dolog, de végülis ott is működik. Ott ugye minden számra S értéke éppen az n-1-es, azaz 1-es maradék (ezt igen ritka esetben szokta az ember használni általában), ami minden számra nulla, viszont 0 helyett mindig n-1-et, azaz 1-et kell venni, tehát 2-es számrendszerben minden számra S értéke 1.
|
| Előzmény: [657] Lóczi Lajos, 2004-12-23 11:00:40 |
|
|
| [656] jonas | 2004-12-21 20:51:57 |
 At kell irni oket kettes szamrendszerbe, hogy konnyen el tudd vegezni bitenkent a logikai muveleteket. (A tizes szamrendszer szerintem nem tartozik magahoz a szamhoz, az csak azt jelenti, hogy irod le oket.)
Ugy ertem, ha nimet jatszol, akkor bitenkenti xor muveletet kell vegezni a nyero strategia meghatarozasahoz, attol fuggetlenul, hogy milyen szamrendszerben irod fel a kovek szamat.
|
| Előzmény: [653] Lóczi Lajos, 2004-12-21 15:05:43 |
|
| [655] Sirpi | 2004-12-21 20:41:19 |
 Dehát S értéke éppen a szám 9-es maradéka, az pedig hatványozás során nyilván periodikus sorozatot ad. És a 2-hatványokon éppen azért egyezik meg S értéke a 11-hatványokéval, mert ugyanazt a 9-es maradékot adják. Más (n-es) számrendszerre elvileg ugyanez megy, ott S értéke épp a szám n-1-es maradéka lesz.
|
| Előzmény: [654] Lóczi Lajos, 2004-12-21 16:34:56 |
|
| [654] Lóczi Lajos | 2004-12-21 16:34:56 |
 A minap hallottam valakitől egy megfigyelést, ebből született az alábbi 130. feladat.
Jelölje S azt a pozitív egészeken értelmezett függvényt, amely egy n számhoz hozzárendeli azt az S(n) pozitív egész számot, amely úgy keletkezik, hogy összeadjuk n (tízes számrendszerbeli) számjegyeit, majd az eredmény számjegyeit ismét összeadjuk, stb., addig folytatva, amíg egyjegyű számot nem kapunk. Tehát pl. S(7331)=5, mert 7+3+3+1=14, és 1+4=5.
Nézzük meg az S függvény értékeit a hatványokon. Azt állítom, hogy az alábbi ismétlődő mintázat keletkezik.
S(11)=1,S(12)=1,...
S(21)=2,S(22)=4,S(23)=8,S(24)=7,S(25)=5,S(26)=1,S(27)=2,S(28)=4,...
S(31)=3,S(32)=9,S(33)=9,...
S(41)=4,S(42)=7,S(43)=1,S(44)=4,S(45)=7,S(46)=1,...
S(51)=5,S(52)=7,S(53)=8,S(54)=4,S(55)=2,S(56)=1,S(57)=5,S(58)=7,...
S(61)=6,S(62)=9,S(63)=9,...
S(71)=7,S(72)=4,S(73)=1,S(74)=7,S(75)=4,S(76)=1,...
S(81)=8,S(82)=1,S(83)=8,S(84)=1,...
S(91)=9,S(92)=9,...
S(101)=1,S(102)=1,...
...
Tehát azt állítom, hogy az 1-hatványokon felvett értékei S-nek ciklikusak, 1-periódussal; a 2-hatványokon felvett értékei S-nek ciklikusak, 6-os periódushosszal; stb. mind-mind periodikusak; sőt, a 10-hatványoktól kezdve az egész eddigi blokk megismétlődik és az ismétlődés folytatódik, tehát pl. S értékei a 11-hatványokon ugyanazok, mint S értékei a 2-hatványokon, stb.
Kérdés: helyes-e az állításom/megfigyelésem?
Mi a helyzet, ha 10-es helyett más számrendszert választok?
|
|
|
|
|
|
|
| [648] Csimby | 2004-12-16 22:01:15 |
 129.feladat
Keressünk összefüggést a Pascal háromszög és a Fibonacci sorozat között.
|
|
| [647] Csimby | 2004-12-16 21:44:11 |
 128. feladat
Egy 8×8-as sakktáblán 8 bástyát helyeztünk el úgy, hogy semelyik kettő sem üti egymást. Bizonyítsuk be, hogy páros sok bástya áll fekete mezőn. (Arany Dani döntő volt, a KöMaL-ban szerepel, de nem mindenkinek jár az újság)
|
|
|
| [644] Szabó Dániel | 2004-12-10 20:02:27 |
 Matekszakkörön találkoztam a következő feladattal: hány olyan 1000000-nál kisebb természetes szám van, melynek a számjegyeinek összege páros, s a nála eggyel nagyobb szám számjegyeinek összege is páros. Leszámoltam Turbo Pascallal, az eredmény 45455. Tanárom szerint 45454. Melyikünknek van igaza?
|
|
|
| [642] Kemény Legény | 2004-12-08 20:43:54 |
 Ha valamelyik ismeretlen 1,akkor a többi is az,és ez megoldás. A 3 egyenlet logaritmusát összeszorozva kapjuk,hogy : xyzlog(x)log(y)log(z)=log(x)log(y)log(z),mivel egyik sem 1(ezt már feltehetjük) xyz=1.Ha nem mind 1: vagy van 2 db 1-nél kisebb vagy lesz 2 db 1-nél nagyobb.Ha pl x és y 1-nél nagyobb: z=x**y>1,azaz xyz>1*1*1=1,nem lehetséges.Ha x és y 1-nél kisebbek z=x**y<1 azaz xyz<1*1*1=1 nem lehetséges.Igy x=y=z=1 a megoldás. (A ** jelöli a hatványozást).
|
| Előzmény: [631] Lóczi Lajos, 2004-11-26 01:04:46 |
|
| [641] Csimby | 2004-12-08 18:39:12 |
 A bal alsó sarokban szereplő számjegy a feltételek miatt nem szerepelhet megegyszer a szürkével jelölt négyzeteken. A skatulya-elv miatt rögtön látszik, hogy mindegyik számjegy pontosan 6-szor kell, hogy előforduljon. Tehát a fennmaradt fehér mezőkön összesen 5-ször kell elhelyezni azt a számjegyet ami a bal alsó sarokban szerepel. Ekkor a két egybevágó fehér rész közül az egyikben 3-szor kell, hogy szerepeljen ez a számjegy. Ez pedig már könnyen látszik, hogy nem lehetséges...
|
 |
| Előzmény: [639] rizs, 2004-12-08 14:28:16 |
|
| [640] rizs | 2004-12-08 14:29:44 |
 Van egy számológépünk, ami kicsit komolyabb, mint egy négyműveletes, tehát tud olyan műveleteket (az inverzeikkel együtt!), hogy gombnyomásra négyzet- és köbgyököt von, van rajta sinus, cosinus, tangens (mindezek hiperbolikus változatai is), 1/x, 10 és e alapú logaritmus, faktoriális. Egy cetlire fel van írva két különböző pozitív egész szám (többjegyű is lehet). Az elsőt még be tudjuk pötyögni a cetliről, de azután már az összes számjegy gombja (0-9) és a tizedesvessző, valamint a négy alapművelet gombja is elromlottnak tekintendő, még az = sem működik. Ezekhez nem szabad nyúlni. A feladat az, hogy csak a rendelkezésre álló matematikai funkciók gombjainak használatával elérjük, hogy a beírt szám helyett előbb-utóbb a cetlin lévő másik pozitív egész szám legyen a kijelzőn. Tehát olyan eljárást kell keresni, amelynek kiindulása az egyik pozitív egész szám, végeredménye pedig a másik, azok értékétől és különbségétől függetlenül. (A kiindulási szám akármennyivel kisebb, de nagyobb is lehet a másiknál.) A módszernek tehát olyannak kell lennie, hogy bármely két pozitív egész számra működjön.
|
|
| [639] rizs | 2004-12-08 14:28:16 |
 sziasztok!
szerintetek lehet rajzolni olyan 6*6-os bűvös négyzetet, amelynek mindegyik sorában, oszlopában és átlójában (átlóként értelmezünk minden átlót, tehát a sarok elemeket, az azok mellett elhelyezkedő 2 elemű átlót, stb.) az 1, 2, 3, 4, 5, 6 számok midegyike legfeljebb 1 alkalommal fordul elő. Természetesen ez azt jelenti, hogy a sorokban, az oszlopokban, és a főátlókban mindegyik szám pontosan egyszer szerepel.
|
|



 0 egyenlőség akkor lép fel, ha a tagok amire alkalmaztuk a közepeket egyenlőek, vagyis x3=2y3=4z3 Ehhez pedig az kell, hogy a tagokban a 2-es azonos kitevőn legyen, vagyis, ha x-ben a-val, y-ben b vel, z-ben c-vel jelöljük a kettőnek a kitevőjét, akkor az alábbi egyenletnek igaznak kell lenni: 3a=3b+1=3c+2 ahol a,b,c egészek. Ez viszont nem lehet soha egyenlő, mert 3-mal osztva különbőző maradékot adnak. Ebből viszont az következik, hogy az egyetlen megoldás a triviális megoldás, ha a x,y,z is 0.
0 egyenlőség akkor lép fel, ha a tagok amire alkalmaztuk a közepeket egyenlőek, vagyis x3=2y3=4z3 Ehhez pedig az kell, hogy a tagokban a 2-es azonos kitevőn legyen, vagyis, ha x-ben a-val, y-ben b vel, z-ben c-vel jelöljük a kettőnek a kitevőjét, akkor az alábbi egyenletnek igaznak kell lenni: 3a=3b+1=3c+2 ahol a,b,c egészek. Ez viszont nem lehet soha egyenlő, mert 3-mal osztva különbőző maradékot adnak. Ebből viszont az következik, hogy az egyetlen megoldás a triviális megoldás, ha a x,y,z is 0. 




 0.
0. 
