|
| [700] Atosz | 2005-01-06 15:38:02 |
 Sziasztok!
Gratulálok Mihály a megoldásodhoz (és Zolinak a magyarázathoz). A gyógyszeres átfogalmazása biztos, hogy nem jó, tulajdonképpen azért amiért te is írtad. Addig is, amíg ezen töprengünk, bedobnék mégegyet, ami szerintem könnyebb: (139.) Van egy 2 tonnás és egy 3 tonnás teherautónk. Egy raktárból kell elszállítani az árut, melyben 5 tonnánál biztosan több cucc van. A csomagokról csak annyit tudunk, hogy mindegyiknek a tömege kisebb mint 1 tonna. (csak a tömegük számít, a méretük, alakjuk nem) A csomagok eloszlásáról nincs információnk. Mennyi az a maximális árumennyiség amit a két autóval egyszerre tutibiztos, hogy el tudunk vinni a raktárból? (Ezt a számot előre kell megmondanunk anélkül, hogy a csomageloszlást látnánk pl. 3.9 tonna stb...) ui: Milyen teherautók esetén mondhatunk legnagyobb számot? (1 és 4 vagy 2.5 és 2.5 stb...) Mi a helyzet több teherautó esetén?
Üdv mindenkinek! Atosz
|
| Előzmény: [699] Fálesz Mihály, 2005-01-06 11:07:42 |
|
| [699] Fálesz Mihály | 2005-01-06 11:07:42 |
 Az átfogalmazás szerintem sem ekvivalens. Az egyes színek (tabletták) kihúzásának valószínűsége nem függhet attól, hogy az adott színű golyóból mennyi van a zsákban (azaz félbetörtük-e már a tablettát). A baj az, hogy nem a golyók, hanem a színek közül kell ugyanakkora valószínűséggel választanunk
Például 2 tabletta esetén az első húzás után 1 fél és 1 egész tabletta marad, a fél tabletta kihúzásának valószínűsége 1/2. Ugyanakkor 2×2 golyó esetén 1/3 a valószínűsége annak, hogy másodszorra éppen az első golyó párját húzzuk ki.
|
| Előzmény: [697] nadorp, 2005-01-06 10:01:48 |
|
| [698] Fálesz Mihály | 2005-01-06 10:55:22 |
 Köszi Zoli,
Örülök, ha helyettem dolgoznak, feltéve, hogy jól. :-)
------
Ami engem a feladat kapcsán izgat, a következő. A megoldás 8 helyett bármilyen 2-hatványra működik. Sőt, 2k-1 tányér esetén is alkalmazható, ha a 0 sorszámú tányért kihagyjuk. De mi a helyzet más számokra? Például 5 tányér esetén? (Bíztató, hogy ha a tányérok száma n, akkor a barát (n+1)-féle lépés közül választhat, tehát a szükségesnél egy kicsit több lehetősége van.)
|
| Előzmény: [695] SchZol, 2005-01-06 09:01:39 |
|
|
| [696] nadorp | 2005-01-06 09:43:04 |
 Megoldás 137-re
A feladat átfogalmazható a következőképppen: Adott egy urna és benne 2n darab golyó. A golyók n-féle színűek és mindegyik szín pontosan 2-szer szerepel. Visszatevés nélkül húzunk az urnábol (2n-2)-szer. Mi a valószínűsége, hogy az urnában maradt 2 golyó azonos színű ?
Ez egy egyszerű kombinatorikai valószínűség.
Az összes eset száma: 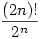
A kedvező esetek száma: 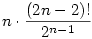
Így a keresett valószínűség: 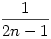
|
| Előzmény: [684] Atosz, 2005-01-04 09:11:00 |
|
| [695] SchZol | 2005-01-06 09:01:39 |
 Sziasztok!
Szerintem jó, amit Mihály ír. XOR művelet annyit tesz, hogy ha azonos helyiértéken páros db 1-es van, akkor 0, ha páratlan, akkor 1 lesz az érték, természetesen bináris számokat nézve. Nézzünk egy példát. A tányérok 0-7ig vannak számozva. Tegyük fel, hogy az 1,4,5,6 balkezes és Hófehérke tányérja a 3-as. Most írjuk fel egymás alá binárisan a balkezes tányérok sorszámát.
Ezeket bitenkét XORolva azt kapjuk, hogy 110. A 3 viszont binárisan 011, tehát egy olyan tányérnál kell megváltoztatni a kanalat, ami az első és a harmadik biten 1-es, vagyis jelen esetben az 5öst átrakjuk a jobb oldalra, így az 1,4,6 össze XORolása pont a 3-at adja.
És ez tényleg jó bármilyen esetre, mert a balkezesek XORolása mindig egy 3bites számot fog megadni, amit egy kanál áthelyezésével tetszőlegesre tudunk állítani, vagyis, úgy hogy pont Hófehérke tányérjának számát mutassák kettes számrendszerben.
Remélem érthető voltam.
Grat Mihály a megoldáshoz és bocsi, hogy beírtam helyetted a magyarázatot.
Üdv, Zoli
|
| Előzmény: [694] lorantfy, 2005-01-06 08:36:31 |
|
|
| [693] Atosz | 2005-01-05 18:19:37 |
 Elsősorban lorantfy-nak (mert ő kérdezte) szól a válaszom. A Hófehérkés feladat mindenféle külső "maszlag" nélkül: Van egy 8 bites 0-kból és 1-esekből álló szám (ami 00000000-tól 11111111-ig bármi lehet) legyen pl.: 01101101 Valaki ezt megmutatja nekem és mond egy általa kigondolt számot 1-8-ig. Én valamelyik bitet ellenkezőre állíthatom, ha akarom (tehát kilenc dolgot tudok csinálni). Ezután bejön a barátom aki szintén először látja ezt a bitsorozatot, majd abból kitalálja a gondolt számot. Olyan terv kell, ami bizonyíthatóan minden bitsorozatra működik. Fálesz Mihály, szerintem itt egy picit te is félreérthetted, úgyhogy próbáld az ötletedet egy kicsit részletesebben kifejteni. Köszi! (attól még jó lehet!) ui: ha sikerül ezt valahogy kifundálnunk, bedobom a további jó feladataimat is! Sziasztok!
|
| Előzmény: [691] lorantfy, 2005-01-05 09:43:24 |
|
| [692] Fálesz Mihály | 2005-01-05 11:58:00 |
 Hát igen. Módosítom a megoldást.
Ötlet: a balkezes tányérok sorszámát XOR-ozzuk össze bitenként. (Nevezzük ezt ,,összegnek''.) Az eredmény adja meg Hófehérke tányérjának számát.
Amikor a barát bemegy, ellenőrzi az összeget. Ha nem stimmel, kiszámíthatja, hogy melyik sorszámot kell hozzávenni/elhagyni, és azt a kanalat helyezi át a tányér másik oldalára.
|
| Előzmény: [691] lorantfy, 2005-01-05 09:43:24 |
|
| [691] lorantfy | 2005-01-05 09:43:24 |
 Üdv Mihály, Atosz és Mindenki!
Jó a Hófehérkés feladat! Én úgy értelmeztem a szöveget, hogy a kanál visszahelyezésénél csak az változhat, hogy a tányér melyik oldalára teszi (jobb, bal). Szóval felvesz egy kanalat az egyik tányér jobb oldaláról és átteszi a bal oldalra vagy fordítva. Ezt jó lenne tisztázni!
|
| Előzmény: [690] Fálesz Mihály, 2005-01-05 08:35:35 |
|
| [690] Fálesz Mihály | 2005-01-05 08:35:35 |
 Egy lehetséges megoldás a 138. feladatra:
A tányérokat megszámozzák 0-tól 7-ig. (Ehhez valamilyen értelmes összebeszélés szükséges, mert a számozáskor még nem látják a tányérok elrendezését. Például az ajtóhoz legközelebbi a 0-dik, és az óramutató járásával ellentétes irányban növekednek a számok.)
A kanalat legalább 8-féleképpen lehet visszatenni: jobb/baloldal, nyelével lefelé/felfelé, a kanál belseje lefelé/felfelé. Ezeket is megszámozzák 0-tól 7-ig.
Hófehérke tányérját a kanalakhoz rendelt számok összege adja meg. A barát úgy helyezi át az egyik kanalat, hogy a kanalak összege ugyanannyi maradékot adjon 8-cal osztva, mint Hófehérke tányérjának a száma. Akár azt is megteheti, hogy már azelőtt felveszi az egyik kanalat, hogy megtudná, melyik Hófehérje tányérja.
|
| Előzmény: [684] Atosz, 2005-01-04 09:11:00 |
|
| [689] Atosz | 2005-01-04 18:07:52 |
 Kedves jonas!
Matematikai modellt adni így tényleg nehéz, de úgy képzeljük el a feladatot, hogy a visszadobás után tökéletes keveredés van, bármelyik darabot egyforma valséggel húzhatjuk ki.
|
| Előzmény: [685] jonas, 2005-01-04 15:30:55 |
|
| [688] Lóczi Lajos | 2005-01-04 17:52:11 |
 Ügyes :)
Ezekkel kapcsolatban tegnap este a bennem legelőször felmerülő kérdés az volt, vajon véletlen-e, hogy az 1729 egyik köbös felbontásában (93+103) és 635318657 egyik negyedik hatványos felbontásában (1334+1344) az egyes alapok között 1 a különbség... Vajon folytatódik-e ez a minta??
|
| Előzmény: [686] jonas, 2005-01-04 16:25:23 |
|
|
|
| [685] jonas | 2005-01-04 15:30:55 |
 137. Erre valószínüleg nehéz pontos matematikai modellt adni. Ugyanis amikor visszadobunk egy fél szem gyógyszert, az fölülre kerül, de a doboz minden mozgatásakor, rázogatáskor a doboz alja felé igyekszik. Ha a dobozt sokat mozgatják, akkor valószínüleg először sok egész gyógyszert veszünk ki, míg ha keveset, akkor sokszor veszünk fél tablettát is.
|
| Előzmény: [684] Atosz, 2005-01-04 09:11:00 |
|
| [684] Atosz | 2005-01-04 09:11:00 |
 Sziasztok!
BÚÉK mindenkinek! Először vagyok itt, nagyon tetszenek az általatok feldobott példák és azok megoldásai. Két feladathoz szeretném kérni a segítségeteket:
137.: Van egy üvegünk, benne 'n' darab gyógyszer. Minden reggel be kell vennünk egy fél szemet. Kiveszünk az üvegből véletlenszerűen egyet ha fél bevesszük, ha egész, akkor kettétörjük, a felét bevesszük a másik felét visszadobjuk. Mennyi a valószínűsége annak, hogy az utolsó szem egész lesz? (tehát amikor már darabra csak 1 van az üvegben, ami vagy fél vagy egész)
138.: A királyfi szeretné megszerezni Hófehérke üvegkoporsóját a törpéktől. Ők azt mondták neki, hogy akkor kapja meg, ha ki tudja választani a tányérját. Az asztalra letesznek nyolc egyforma tányért (Hófehérkéjét és a törpékét), mindegyik mellé egy-egy kanalat jobbra vagy balra aszerint, hogy az illető jobb vagy balkezes, majd rámutatással válassza ki a nyolc közül Hófehérkéjét. A királyfi összebeszélt a barátjával, aki a választás előtt bement a szobába és kérte a törpéket, hogy mutassák meg a tányért neki. Miután megtudta, hogy melyik Hófehérkéjé, felvett egy kanalat nézegette. A törpék rászóltak, hogy tegye vissza. Ő visszatette a tányér mellé vagy oda ahol volt, vagy a másik oldalra (ezt a törpék nem vették észre). Ezután bejött a királyfi és kis tanakodás után határozottan rámutatott Hófehérke tányérjára. Hogyan csinálták? (természetesen matematikai trükkről van szó)
Az első feladatra csak egy rekurzív képletet tudtam gyártani (úgy gondolom, hogy ez nehéz példa), míg a másodiknál nyomon vagyok, de nincs meg tökéletes megoldás. Ha valamelyikőtöknek bármilyen ötlete (megoldása) van várom!
|
|
| [683] SAMBUCA | 2005-01-04 02:48:42 |
 Kedves rizs!
Ha jól tudom, akkor az általad kitüzött 136. feladat a tavalyi Kürschákon volt a 3. feladat. A megoldás megtalálható itt a KöMaL fórumon: Nehezebb matematikai problémák topic, Kemény Legény 96. hozzászólása.
SAMBUCA
|
| Előzmény: [682] rizs, 2005-01-04 01:32:40 |
|
| [682] rizs | 2005-01-04 01:32:40 |
 Kedves Lajos! Köszi az előzőt!
136.: Van egy körvonalunk, van rajta 2 kék pötty. Kék és piros pöttyök játszanak, és ezek csak körvonalon lehetnek. Két műveletet végezhetünk: - Két bármilyen pötty közé betehetünk egy pirosat, és ekkor ennek a két szomszédja színt vált. - Ha van legalább 3 pöttyünk, akkor egy piros pöttyöt elvehetünk, és ennek két szomszédja színt vált. A kezdeti 2 kék pöttyből a fenti műveletekkel eljuthatunk-e olyan álláshoz, hogy csak 2 piros pötty legyen?
|
|
| [681] Lóczi Lajos | 2005-01-04 01:28:51 |
 135. feladat: Keressük meg azt a legkisebb pozitív egészt, amely kétféleképpen írható fel két pozitív egész negyedik hatványának összegeként (a sorrendcsere persze nem számít különböző felírásnak...)
Segítség: a keresett számnak pontosan 4 db, 1000 alatti prímtényezője van.
A megoldásból, összevetve a köbökre vonatkozó kérdéssel máris további sejtések hada fogalmazható meg...különös dolog ez a számelmélet:)
|
| Előzmény: [680] Lóczi Lajos, 2005-01-04 01:10:08 |
|
| [680] Lóczi Lajos | 2005-01-04 01:10:08 |
 Ó, persze hogy vannak, de még milyen sokan...
Először Mathematicával megkerestem a legkisebb ilyet, ami az 1729, ekkor beugrott: oppá, Ramanujan, ezt vele kapcsolatban olvastam.
A híres anekdota megtalálható pl. itt http://mathworld.wolfram.com/Hardy-RamanujanNumber.html
sok-sok más csemegével és érdekességgel...
Az 1729 utáni következő néhány, kérdezett tulajdonságú szám egyébként rendere: 4104, 13832, 20683, ... stb.
|
| Előzmény: [679] rizs, 2005-01-03 23:11:32 |
|
| [679] rizs | 2005-01-03 23:11:32 |
 Szeretném újra felvetni egy régebben javasolt, de visszhangot nem látott feladatomat: Melyik az a legkisebb x pozitív egész, amely kétféleképpen is felbontható 2 pozitív köbszám összegére? Van-e egyáltalán ilyen? Ja és Kyle's Mom Is A Big Bad Itch :D
|
|
|
|












 VI, ez akármilyen modulusra igaz...
VI, ez akármilyen modulusra igaz...