|
| [788] Lóczi Lajos | 2005-02-18 03:08:28 |
 Miért kellett akkor ilyen bonyolult megoldást adni? :) Ezen az alapon szinte bármely gyufát elmozdítva "igaz" egyenlőséget kapunk, ami 0, vagy 1 vagy 2 tizedesjegyre pontos...
|
| Előzmény: [787] ScarMan, 2005-02-17 18:31:45 |
|
|
|
| [785] manó | 2005-02-17 17:41:03 |
 Sziasztok! Én új vagyok itt, és nem is mozgok otthonosan ebben a témában, de gondoltam ti tudnátok segíteni. Van egy egyszerű, gyufarejtvényes problémám, amit holnap délig meg kellene oldani! A feladat: egy gyufaszál elmozdításával tedd igazzá az egyenletet: XXII/VIII=II (a VIII persze a XXII alatt van, csak nem tudom, hogy lehet itt úgy ábrázolni:)) Szóval bennetek van minden reményem! Köszi!
|
|
|
| [783] Fálesz Mihály | 2005-02-16 11:23:23 |
 Az egyik hírportálon, ahol gyakran jelennek meg matematikai bulvárhírek is (ezek színvonala messze az átlagos bulvárhírek alatt marad), tegnap megjelent egy hír, miszerint Bezdek Károly fia, Dániel bebizonyított egy 500 éves sejtést. A cikkben így fogalmaznak:
| ,,... A 16. század kezdetén, ábrázolásgeometriai vizsgálódásai közben Dürerben felmerült a kérdés, hogy vajon minden poliéder (térbeli, sík lapokkal határolt mértani test) kiteríthető-e úgy, hogy lapjai sehol sem fedik egymást. ...'' |
|
Én ezt úgy értem, hogy a poliédert bizonyos élei mentén felvágjuk és síkba hajtogatjuk, és nem csak konvex, hanem konkáv poliéderek (akár tóruszszerűek is) megengedettek.
149. feladat. Mutassunk példát olyan poliéderre, ami nem teríthető ki. :-)
|
|
| [782] SAMBUCA | 2005-02-11 01:35:23 |
 Helló Mindenki!
Kissé fel lehet tuningolni a 147. feladatot:
148. feladat: 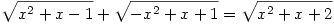
Üdv. SAMBUCA
|
|
| [781] Kemény Legény | 2005-02-11 01:29:34 |
 A feladat nyilván a valós megoldásokat kérdezi, hiszen csak ekkor van értelme a gyökjelnek. A bal oldalon 2 szám összege szerepel, erre a 2 számra alkalmazva a számtani-négyzetes közepek közötti egyenlőtlenséget kapjuk, hogy 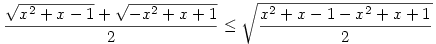 , azaz a baloldal legfeljebb , azaz a baloldal legfeljebb 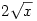 .Mivel mindkét gyök alatti kifejezés nemnegativ, ezért összegük, 2x is az, azaz x nemnegativ. Ha x 1-nél kisebb, .Mivel mindkét gyök alatti kifejezés nemnegativ, ezért összegük, 2x is az, azaz x nemnegativ. Ha x 1-nél kisebb, 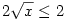 , azaz a baloldal bőven kisebb mint a jobb, ha pedig x 1-nél nagyobb, akkor , azaz a baloldal bőven kisebb mint a jobb, ha pedig x 1-nél nagyobb, akkor 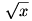 -nél nagyobb az x és x2 is, igy ismét kisebb a baloldal, mint a jobb. Ha pedig x=1 az nem megoldás, igy nincs valós megoldása az egyenletnek....... -nél nagyobb az x és x2 is, igy ismét kisebb a baloldal, mint a jobb. Ha pedig x=1 az nem megoldás, igy nincs valós megoldása az egyenletnek.......
|
| Előzmény: [780] lorybetti, 2005-02-10 21:52:58 |
|
| [780] lorybetti | 2005-02-10 21:52:58 |
 147.feladat: Az Erdős Pál Matematikai Iskolában volt kitűzött feladat:
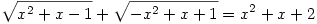
|
|
| [779] Kemény Legény | 2005-02-08 15:07:01 |
 Elnézést mindenkitől,de sajnos tévesen irtam azt,hogy a 3szögek sorozata akkor konvergál egy ponthoz,ha a végtelen sok véletlenszerüen választott 0..1 közti szám szorzata 0-hoz tart.Ugyanis ha az oldalon az arány x,akkor az új 3szög területe 1-3x(1-x) szerese lesz az elözönek.Igy az kell,hogy ha az x-eket véletlenszerüen választjuk,milyen eséllyel tart az 1-3x(1-x) számok szorzata 0-hoz.ezek pedig nem véletlenszerüen vannak kivál.va 0..1röl,hiszen pl.mindegyikük legalább 1/4.Szerencsére azonban itt is az 1/4..1/2 int.vallumba 1 val.szinüséggel esik végtelen sok,mert ehhez az kell hogy 1/4<1-3x(1-x)<1/2 teljesüljön az x-re.Ez a feltétel x-re nézve 2 int.vallumot ad,azokba pedig 1 val.szin.gel végtelen sok x fog esni,igy az 1-3x(1-x) ek közt 1 val.szin.gel végtelen sok lesz az 1/4..1/2 int.vall.ban,igy a szorzatuk 0-hoz tart 1 val.szin.gel.
|
| Előzmény: [771] Kemény Legény, 2005-02-06 19:48:18 |
|
| [778] Káli gúla | 2005-02-07 23:05:16 |
 Folytatva a súlypont körüli asszociációs játékot :
146. feladat. Bizonyítsuk be, hogy minden konvex sokszög belsejében van olyan P pont, hogy minden, P-n átmenő AB húrra
AP/BP 2 2
.
|
|
| [777] Atosz | 2005-02-07 18:21:40 |
 Kedves jenei.attila!
A gyógyszeres feladat jelenleg pihen, bár lehet, hogy néhányan törik rajta a fejüket. Annyi eredményünk van, amennyi eddig a fórumon elhangzott, azaz p2,k kivételével csak egy általános rekurzív alak. Könnyen lehetséges, hogy nincs zárt alakban megoldás. A feladatot én találtam ki évekkel ezelőtt egy unalmas matekórán, s néha-néha előszedtem egy kicsit. Azért tettem fel ide a fórumra, hátha valakinek bevillan valami okos ötlet. Egyelőre úgy tűnik, hogy kifog rajtunk, de sosem szabad feladni, mint ahogy Wiles sem engedte ki a markából a Fermat tétel bizonyítását. A kettő között mindössze annyi különbség van, hogy annak megoldása a matematika sok területét kapcsolta össze, míg ez valószínűleg csak egy jelentéktelen zsákutca. Én már annak is örülnék, ha pl. közelítő megoldás, vagy valami ügyes rekurziós átalakításunk lenne, vagy a spec esetek száma bővülne (pl. zárt alak pk,k-ra.)
Minden jót!
|
| Előzmény: [776] jenei.attila, 2005-02-07 12:07:01 |
|
| [776] jenei.attila | 2005-02-07 12:07:01 |
 Szia Atosz!
A gyógyszeres feladattal hogy állunk? A rekurzió megoldása elég reménytelennek tűnik. Lehetséges egyáltalán szép zárt alakot adni rá? Vagy esetleg valami ügyes trükkel (ld. őrült légi utasok) egyszerűbben megoldható? Egyébként honnan származik a feladat?
|
|
| [775] Kemény Legény | 2005-02-07 10:44:47 |
 Végtelen sok véletlenszerüen választott 0..1 közti szám között 1 val.szinüséggel lesz végtelen sok a 0..1/2 intervallumban,ekkor pedig a szorzat csak 0-hoz tarthat.Igy 1 a val.szine annak hogy 0 lesz a szorzat.
|
| Előzmény: [774] Atosz, 2005-02-07 09:01:53 |
|
| [774] Atosz | 2005-02-07 09:01:53 |
 Teljesen igazad van, becsapott az an sorozat, ami minden 0 és 1 közötti a esetén 0-hoz tart. Így viszont, jogosnak tűnik Kemény Legény felvetése, miszerint ha véletlenszerűen választunk számokat a (0,1) intervallumból, akkor milyen valséggel lesz a szorzat 0-tól különböző.
|
| Előzmény: [773] Sirpi, 2005-02-07 01:19:36 |
|
| [773] Sirpi | 2005-02-07 01:19:36 |
 Azt viszont furcsálnám, ha 1-nél kisebb számok szorzata nem tartana a nullához.
Miért is? Legyen mondjuk 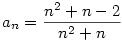 , ami szemlátomást szigorúan 0 és 1 közé esik, ha n legalább 2. Ekkor az an-ek szorzatának határértéke nem nulla lesz. Gyakorlásképpen, akinek van kedve, számolja ki a szorzat határértékét, mondjuk a 2. tagtól kezdve (n=1-re an=0, tehát úgy nem lenne túl nehéz szorzatot számolni). , ami szemlátomást szigorúan 0 és 1 közé esik, ha n legalább 2. Ekkor az an-ek szorzatának határértéke nem nulla lesz. Gyakorlásképpen, akinek van kedve, számolja ki a szorzat határértékét, mondjuk a 2. tagtól kezdve (n=1-re an=0, tehát úgy nem lenne túl nehéz szorzatot számolni).
|
| Előzmény: [772] Atosz, 2005-02-06 23:27:49 |
|
| [772] Atosz | 2005-02-06 23:27:49 |
 Kedves Kemény Legény!
Gratulálok a megoldáshoz! Ez tulajdonképpen egy ujjgyakorlat volt "szörnyűnek" tűnő megfogalmazásban. Szerintem azért ez egy érdekes tulajdonsága a súlypontnak. Azt viszont furcsálnám, ha 1-nél kisebb számok szorzata nem tartana a nullához.
|
| Előzmény: [771] Kemény Legény, 2005-02-06 19:48:18 |
|
| [771] Kemény Legény | 2005-02-06 19:48:18 |
 Legyenek az A0B0C0 csúcsaiba mutató helyvektorok:a,b,és c.Ekkor az A1 pont helyvektora kifejezhető a és b lin.komb.jaként,mégpedig ax+by alakban ahol x+y=1.Ekkor B1,C1 pontok helyvektorai: bx+cy ill.cx+ay lesznek. Az eredeti 3-szög súlypontja (a+b+c)/3,mig az új 3-szögé: (ax+by+bx+cy+cx+ay)/3=(a+b+c)(x+y)/3=(a+b+c)/3 lesz. Igy a müvelet során a háromszögek súlypontjai változatlanul maradnak,és mivel a háromszög súlypontja általában a belsejébe szokott esni,ezért ha a 3-szögek végtelen sorozata egyáltalán konvergál vmely ponthoz(elég ha a területük tart 0-hoz,mivel egymásba skatulyázott zárt halmazok),akkor az a háromszög súlypontja lesz.Az már persze nem geometriai kérdés hogy végtelen sok véletlenszerüen választott 0 és 1 közti szám szorzata milyen eséllyel tart 0-hoz,hiszen csak ekkor konvergálhat a 3-szögsorozat vhová.
|
| Előzmény: [770] Atosz, 2005-02-04 09:52:18 |
|
| [770] Atosz | 2005-02-04 09:52:18 |
 145. feladat Vegyünk egy tetszőleges A0B0C0 háromszöget, majd ennek A0B0 oldalán véletlenszerűen válasszunk ki egy pontot, legyen ez A1. Amilyen arányban felosztja A1 az A0B0 oldalt, ugyanilyen arányban (és megfelelő sorrendben) vegyük fel a B1 és C1 pontokat a megfelelő oldalakon. Így kapjuk az A1B1C1 háromszöget. Az eljárást kezdjük előlről (már az új háromszögön - újra véletlenszerű választással) és folytassuk a végtelenségig. A kérdés az, hogy a háromszögeknek ez a végtelen sorozata az eredeti háromszög mely belső pontjához konvergál?
|
|
| [769] Káli gúla | 2005-01-31 23:30:02 |
 A
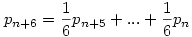
rekurzió megoldására gondoltam (bár elismerem, az "igazi" jelző kicsit erős volt :)
Nézzük, mi lenne, ha nem a (0,0, ... , 1) kezdeti feltételekkel indulnánk. Vegyük az (1,0,...,0)-hoz tartozó 1,0,...,0,1/6, . . . sorozatot. Az első elemet elhagyva a 0,..,0,1/6, . . . sorozatot kapjuk, tehát (1,0,..,0)-ról indulni pontosan ugyanaz, mint (0.0,...,1/6)-ról. Hasonló összefüggést kaphatunk a többi kezdeti feltételre is (felhasználva a megoldásoknak a kezdeti feltételtől való lineáris függését). Jelöljük a (0,..,1,..,0) j-edik egységvektorral induló megoldást Ej-vel. Tegyük fel, hogy létezik a keresett határérték (lim E6(n) = p). Legyen az első elem elhagyása (a léptetés operátor) T. Világos, hogy TEj(6) = Ej(7) = 1/6 (j=1,..,6), ezért
E1 TE1=1/6E6 TE1=1/6E6 1/6p 1/6p
E2 TE2=E1+1/6E6 TE2=E1+1/6E6 2/6p 2/6p
E3 TE3=E2+1/6E6 TE3=E2+1/6E6 3/6p 3/6p
E4 TE4=E3+1/6E6 TE4=E3+1/6E6 4/6p 4/6p
E5 TE5=E4+1/6E6 TE5=E4+1/6E6 5/6p 5/6p
E6 6/6p 6/6p
Ezeket összeadva, E1+...+E6 1 miatt 1 miatt
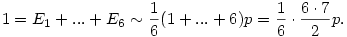
* * *
Be kell még látni, hogy minden megoldás konvergens. Ehhez felhasználhatjuk azt a tulajdonságot, hogy a számtani közép nem kerülhet túl közel a számhalmaz széléhez, pontosabban, ha a xj xj b (j=n+1,...,n+6), akkor a+d/6 b (j=n+1,...,n+6), akkor a+d/6 M M b-d/6, ahol d=b-a és M az xj (j=n+1,...,n+6) számok számtani közepe. Így, ha a sorozat elemeit hatosával blokkokra osztjuk, az egyes blokkok mindig az előző blokk által feszített intervallum középső kétharmadába esnek. b-d/6, ahol d=b-a és M az xj (j=n+1,...,n+6) számok számtani közepe. Így, ha a sorozat elemeit hatosával blokkokra osztjuk, az egyes blokkok mindig az előző blokk által feszített intervallum középső kétharmadába esnek.
|
| Előzmény: [768] Atosz, 2005-01-30 19:21:54 |
|
| [768] Atosz | 2005-01-30 19:21:54 |
 Kedves Káli gúla!
Köszönöm a gratulációt! Egyébként ez volt a te "igazi" megoldásod is, vagy a rekurziós?
|
|
| [767] Káli gúla | 2005-01-30 11:57:12 |
 Kedves Atosz, bocs, újraolvasva, teljesen jó ahogy írtad. Mindegy, hogy időben az első, vagy az utolsó mező szerint számolunk.
Kedves Kemény Legény, kösz a hivatkozást. A konvergencia bizonyítással a végén tényleg nem sokat epszilonozik.
|
|
| [766] Káli gúla | 2005-01-30 10:46:30 |
 Igen, grat! Annyi kiegészítéssel, hogy Ai az az esemény legyen, amikor utoljára mondjuk, hogy most már elég egy dobás.
Általánosabban, 6 helyett k-ra, egy k hosszú szakaszba való bekerülés valószínűsége egy. Az elhagyó (utoljára érintett) mező szerint osztályozva
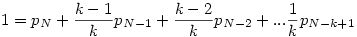
Így, ha tudjuk, hogy lim pN=p létezik, akkor
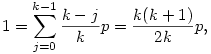
ahonnan p=2/(k+1), éppen a lépéshossz várható értékének a reciproka.
|
| Előzmény: [765] Atosz, 2005-01-30 08:22:27 |
|
| [765] Atosz | 2005-01-30 08:22:27 |
 Sziasztok!
Azt hiszem meg van a megoldás. Káli gúla hozzászólása ébresztett rá arra, hogy egy szomszédos 6-os tartományba lépés valsége nagyobb mint 1, hiszen ezek nem függetlenek egymástól. Az utolsó dobás alapján elkezdtem a rekurziót visszafejteni és kaptam, hogy
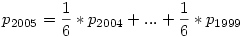
Ez azt jelenti, hogy a sorozat mindig az előző hat átlagával halad tovább és mivel az elejét ismerjük így onnan elindulva kiszámítható, hogy mennyi lesz p2005
Viszont ennél találtam egy gyorsabb megoldást is! Tekintsük azokat az eseményeket, amikor kimondom azt, hogy most már 1 dobással is beérhetek a célba. Ez 6 helyet jelent a 2005-ik előtt. Legyen Ai az az esemény, hogy a (2005-i)-ik helyen szólalok meg (i=1,...,6). Ezen események valségei pAi nem egyeznek meg a rálépés valségével, viszont függetlenek és összegük 1. Legyen ilyen távolságban a mezőre lépés valsége p (feltesszük, hogy már közel egyforma - éppen ezt keressük). A 2004-ik helyen akkor szólalok meg, ha előtte ráléptem az 1998-ikra és ott 6-ost dobtam, azaz 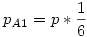 . A 2003-ik helyen akkor szólalok meg, ha az 1998-ik helyről érkezem 5-össel, vagy az 1997-ről 6-ossal, azaz . A 2003-ik helyen akkor szólalok meg, ha az 1998-ik helyről érkezem 5-össel, vagy az 1997-ről 6-ossal, azaz 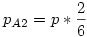 , stb... , stb...
Ha ezt mind felírjuk, kapjuk hogy
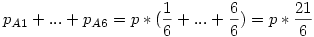
Mivel ez 1, így
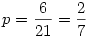
Természetesen ez csak akkor lesz pontosan igaz, ha a kérdéses hely tart a végtelenbe, de a 2005. már "jó közelítéssel" ennek tekinthető.
|
|









 2
2

 TE1=1/6E6
TE1=1/6E6 1 miatt
1 miatt