| [851] tudniakarok | 2005-03-28 23:22:47 |
 Őszintén szólva,én is az "elegánsabb" megoldás reményében írtam be a feladatom,mert az én bizonyításom is legalább ilyen hosszú.Ettől függetlenül én is csak az elejét értem a bizonyításodnak...(mondjuk Einsteint sem értették:) Talán vmi ábrával szemléltetve felfognánk mit mondasz!?
|
| Előzmény: [849] levi, 2005-03-28 15:15:47 |
|
| [850] jonas | 2005-03-28 21:57:55 |
 Ezt a bizonyítást nem egészen értem. Az világos, hogy ha a legfelső sorban három lyuk van, akkor nem lehet a következőben egynél több. Viszont úgy tűnik, hogy a bizonyîtásban ezt nem csak az első sorra, hanem a többire is kihasználod, ezekre pedig már nem tudon, miért lenne igaz.
|
| Előzmény: [849] levi, 2005-03-28 15:15:47 |
|
| [849] levi | 2005-03-28 15:15:47 |
 Elképzelés a 158. feladatra: Tehát próbáljunk meg 14 üres mezőt úgy elhelyezni ezen a táblázaton, hogy a maradék 22-n mind legyen dominó. Mivel 6 sorunk és oszlopunk van, belátható, hogy 2 sorban és oszlopban legalább 3 üres mező lesz. Azt kell belátnunk, hogy nem tudunk úgy elhelyezni 14 üres mezőt, hogy a nem üreseket pedig dominó fedje. Vizsgáljuk csak a sorokat! Ha az első sorban 3 üres mezőt kívánunk elhelyezni, azt kétféleképpen tehetjük meg: (D a dominóval fedett, Ü az üres mező): (1) ÜDÜDÜD (vagy ennek szimmetrikus változata) ill. (2)ÜDÜDDÜ (és ennek is a szimmetrikus változata). A szimmetrikus változatok vizsgálatát elhagyhatjuk, hiszen azok lényegében ugyanazok mint az eredetik. Először nézzük meg, hogy ha egy sorban 3 üres mező van, akkor a következő sorban mennyi üres mező lehet maximum. Az (1) esetén 0, míg a (2) esetén 0 vagy 1. Nézzük az (1) elrendezést! Ekkor a második sorban DDDDDD lesz, hiszen az első sor 1.,3.,5. kockája alatt nem lehet üres mező, mert akkor lenne üres pár, így a második sor 1.,3.,5. mezője D-s lesz, a 2.,4.,6. mező pedig az első sor dominói miatt lesznek fedettek. Tehát a maradék 4 sorban 11 üres mezőt kellene elhelyeznünk. Mivel egy sorban 0,1,2,3 üres mező lehet és a 11-et 4 tag összegeként a 0,1,2,3 segítségével csak 2+3+3+3-ként lehet felírni, ezért a maradék 4 sorból háromban is 3 üres mezőnek kell szerepelnie. De ha a 3. sorban 3 üres mező van, akkor a következőben legfeljebb egy lehet, azaz a hátramaradó kettőben 7nek kell lennie, ami lehetetlen. Ha a harmadik sorban 2 üres mező van, akkor a negyedik már biztos 3 van, de az után legfeljebb csak egy lehet az ötödikben, azaz a hatodikban 5nek kell lennie, ami szintén lehetetlen. A (2) esetben a 2. sorban a legjobb esetben 1 üres mező szerepel. Az a maradék négy sorban 10. Ez kétféleképpen írható fel a 0,1,2,3 számok 4tagú összegeként: 1+3+3+3 vagy 2+2+3+3. Erről a két lehetőségről is könnyen beláthatjuk, hogy nem lehetségesek (hasonlóan mint az (1) esetben). Ha az első sorban 2 üres mező szerepel, azzal nem változott semmi, hiszen a 2 db 3 üres mezős sor elhelyezése abban az esetben sem lehetséges. Tehát beláttuk, hogy nem lehet elhelyezni 14 üres mezőt, úgy hogy a maradék 22-n mind dominó legyen, azaz legalább egy üres mező-pár lesz, azaz elhelyezhetünk még egy dominót úgy, hogy ne kelljen elmozdítani amár lerakott dominókat. (Picit hosszú megoldás, jobb lett volna egy rövidebb, "elegánsabb", de olyat nem találtam... talán valaki más...)
|
| Előzmény: [848] tudniakarok, 2005-03-27 11:42:56 |
|
| [848] tudniakarok | 2005-03-27 11:42:56 |
 Egy unalmas irodalomóra szüleménye!(szerintem érdekes lett)
158. feladat: Egy 6x6-os táblázatra néhány dominót helyezünk, hogy mindegyik pontosan 2 mezőt fed le. Bizonyítsuk be,hogy ha 14 mező fedetlen,akkor még egy dominót a táblára helyezhetünk,úgy hogy a többit a helyén hagyjuk!
|
|
|
| [846] Kemény Legény | 2005-03-17 16:47:25 |
 Na egy érdekes feladat:Lehet-e 6 egymást követő pozitív egész szám szorzata egy egész szám 5. hatványa?
|
|
| [845] Lady | 2005-03-15 11:39:38 |
 (4x+3)(x-5).3=(2x+21)(x-2).6 Vezesd le a következő lépést.Kösz
|
|
|
|
|
| [841] jonas | 2005-03-11 16:57:16 |
 Ez érdekes. Hárommal persze meg tudom csinálni (veszek három egymásra merőleges téglalapot úgy, hogy a csúcsaik egy szabályos ikozaéder csúcsait alkossák, és ezeknek a kerülete megfelel), de nem tudtam, hogy háromnál többel is lehet.
|
| Előzmény: [839] Atosz, 2005-03-10 16:34:37 |
|
| [840] Hajba Károly | 2005-03-10 16:48:01 |
 Üdv Atosz!
Ne is! Aki nem ismeri, hadd gondolkozzon rajta. A megoldhatóság is egyfajta segítség már. Én is azután tudtam megoldani, miután közölték, hogy létezik megoldás. :o)
HK
|
| Előzmény: [839] Atosz, 2005-03-10 16:34:37 |
|
| [839] Atosz | 2005-03-10 16:34:37 |
 Kedves Onogur!
Nem csak hármat, akármennyit lehet úgy, hogy szétnyitás nélkül megbonthatatlanul egyben marad, de bármelyiket nyitjuk, darabjaira hullik az egész. Még nem rajzolom be a megoldást, mert ismerem a feladatot!
|
| Előzmény: [838] Hajba Károly, 2005-03-10 11:54:41 |
|
| [838] Hajba Károly | 2005-03-10 11:54:41 |
 Kedves Betti!
Köszi a kiegészítést.
157. feladat:
Lehet-e 3 karikát nem szétesően úgy egymásba fűzni, hogy bármelyik kinyítása esetén a másik kettő is szabaddá válik.
HK
|
|
|
|
| [835] Hajba Károly | 2005-03-09 09:30:49 |
 Csak nem egy viharfelhő, akarom mondani 2 szintű elektronfelhő síkmetszete. Nem. Egy metapárt szimboluma (CS-NY-P). De ez sem. Inkább egy részeg nyolcas. Szóval a megoldás végtelen. :o)
HK
|
| Előzmény: [834] Lóczi Lajos, 2005-03-08 22:11:47 |
|
| [834] Lóczi Lajos | 2005-03-08 22:11:47 |
 156. feladat: Mi lesz az x2-y2=1 egyenletű hiperbola képe annál az inverziónál, melynek alapköre az origó középpontú egységkör?
|
|
| [833] Atosz | 2005-03-07 18:30:42 |
 Kedves Onogur!
Én inkább egy olyan bonyolításon törtem a fejem, hogy ugyanígy 2 gyerek és 1 kutya van, csak a sebességeket kellene belőni úgy, hogy minél hamarabb jussanak át mindhárman, annyi megkötéssel, hogy a gyalog-sebességek összege legyen 8 km/h, a bicaj-sebességek összege pedig legyen 40 km/h. Azaz az eredeti feladat szerinti sebességösszegeket kellene szétosztani hármójuk között úgy, hogy minél hamarabb átjussanak.
Természetesen előbb kiszámoljuk a tiedet, majd utána jöhet ez.
Lászlónak! Örülök, hogy tetszenek a példák - bár én tudnék ilyeneket kitalálni - a lényeg az, hogy én pont azokat kedvelem, melyeket egyszerűen meg lehet fogalmazni, mégis az első gondolatunk esetleg tévútra vezet. (lehetetlennek tűnik)
|
| Előzmény: [832] Hajba Károly, 2005-03-07 15:47:53 |
|
| [832] Hajba Károly | 2005-03-07 15:47:53 |
 155. feladat:
Bonyolítsuk tovább Atosz 153. feladatát; most találtam ki, lehet, hogy tele lesz törttel:
A, B, C és D személy közösen 20 km útra indulnak 1 biciklivel. 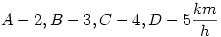 sebességgel képes haladni, míg a bringával mindenki sebességgel képes haladni, míg a bringával mindenki 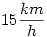 sebességgel képes haladni. Mennyi idő alatt tudnak leghamarabb célba érni? sebességgel képes haladni. Mennyi idő alatt tudnak leghamarabb célba érni?
HK
|
|
|
| [830] lorantfy | 2005-03-07 14:02:13 |
 Kedves Atosz!
Jók a példák! Főleg a bicajos. Ha lesz egy kis időm átdolgozom egy kicsit, hogy lehessen csomagtartón is szállítani...
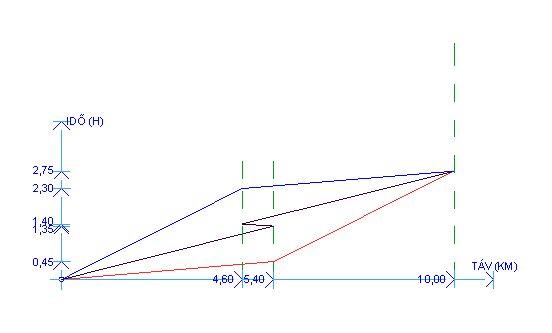
153. feladathoz: A szöveg ábrává formálva itt látható. Ebből már könnyű felírni az egyenleteket. A D-vel és E-vel jelölt eltelt idők mindkét személynél egyenlőek. A megoldás x=11.
![[x+\frac{9y}{4}-(86-x)]\frac{15}{16}=86-x](keplet.cgi?k=B9C141C7734E6914)
2y-x=y-(86-x)
|
 |
| Előzmény: [829] Atosz, 2005-03-07 09:14:54 |
|
| [829] Atosz | 2005-03-07 09:14:54 |
 Sziasztok!
László, nagyon ötletes - és jó! - a levezetésed a bicajos feladatra. Remélem megtetszett! Természetesen megvalósítható (matematikai értelemben persze - lopás kizárva): Az egyik gyerek 5.4 km-t teker előre, majd a kutya 0.8 km-t vissza. Így mindhárman egyszerre érkeznek be.
Természetesen a másik feladatra adott megoldásod is jó, így csak gratulálni tudok!
|
| Előzmény: [828] lorantfy, 2005-03-07 01:25:20 |
|
| [828] lorantfy | 2005-03-07 01:25:20 |
 Kedves Atosz!
Hát persze, hogy a 153. feladatot is megcsináljuk. Már korábban a suliban egyik szünetben próbálkoztam vele, de nem lett egész és egy életkoros feladatban nem egész szám csak az emeltszintű érettségin lehet, így elment a kedvem tőle.
Aztán most felszólításodra átolvastam mégegyszer és kijött, hogy én 75 éves vagyok, kis barátom meg 11 éves. Aki nem hiszi, járjon utánna!
|
| Előzmény: [826] Atosz, 2005-03-06 18:38:23 |
|
| [827] lorantfy | 2005-03-06 23:49:20 |
 Hello Csimbi!
Kösz az ötletet. Hogy én erre nem jöttem rá :-) Ebből is látszik, hogy a vasárnapi ebéd után kevés vér jut az ember agyába.
Hát akkor kerékpározzon visszafelé a kutyus attól a ponttól, ahol Juliska hagyta a bicajt, mondjuk t ideig. Így 16t utat tesz meg, ezt visszafelé 4 km/h sebességgel 4t alatt fogja megtenni, vagyis 5t idővel nő a menetideje.
És mennyit nyer rajta a két gyerek. A 16t utat kettőjük között egyenlően kell elosztani. Tehát Juliska 8t-vel tovább megy mint az út fele. A kutya visszahozza 16t-vel és így Jancsi is 8t-vel többet biciklizhet. Most a 8t utat 2 km/h helyett 12 km/h sebességgel tudja megtenni, így a nyereség 8t/2 - 8t/12 = (10/3)t
Az előző gondolatmenet szerinti menetidők különbsége 25 perc volt. Növelje a kutyus annyivel a menetidejét, hogy éppen egyenlő legyen Jancsi és Juliska új csökkentett menetidejével, így pont együtt fognak beérni.
(10/3)t+5t = 25perc, amiből t=3perc, akkor 5t=15-perccel nő a kutya menetideje és ennyi lesz J és J ideje is.
Tehát az elérhető csúcsidő: 2 óra 45.
Az első gyerek akkor 5+8t=5+24/60 = 5,4 km-ig kerekezik és ott leteszi a bicajt.
Hát, gondoljátok végig, hogy ez megvalósítható-e! (Mi van ha közben ellopják a kerékpárt?)
Az lenne még kutyajó, ha a kerékpáron lenne csomagtartó és egyik szállíthatná a másikat!
|
| Előzmény: [825] Csimby, 2005-03-06 15:23:15 |
|