| [876] Csimby | 2005-04-17 21:02:14 |
 Ezt most találtam, Ramanujan egyik formulája. Csak érdekességnek rakom fel, szép nem?
|
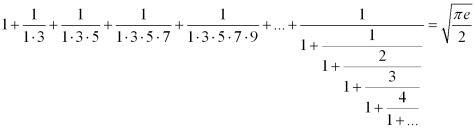 |
|
| [875] Hajba Károly | 2005-04-08 15:28:33 |
 Kedves (mindent) tudniakarok!
Egy újszülöttnek minden vicc új, de nem a véneknek. :o) Szóval anno, valamikor a '90-es években valamelyik magyar ált. isk. diákjai lelkes matektanáruk irányításával egy nagyszabású kisérletet tettek a betetted feladat megvalósítására. Két napon keresztül többezer gyufaszálat v. akármit ejtegettek le több csoportba szerveződve. Ha jól emlékszem 2 tizedesjegy pontossággal ki is hozták a  értékét. Ez akkor világcsúcs volt. értékét. Ez akkor világcsúcs volt.
Érdekes lehet az betett ábra egyéb formái is.
HK
|
| Előzmény: [874] tudniakarok, 2005-04-08 14:11:29 |
|
| [874] tudniakarok | 2005-04-08 14:11:29 |
 Na ez érdekes,nagyon...
159.feladat: Tulajdonképpen a feladat nem más, mint egy kísérlet, amit egy Buffon nevű matematikus agyszüleményeként tartanak számon:
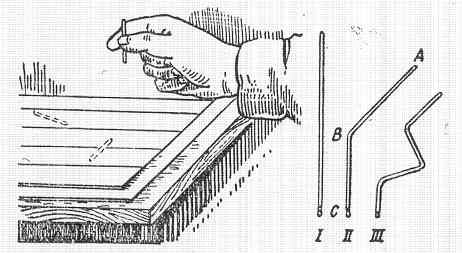
Felszereljük magunkat egy rövid, kb. 2 cm hosszú varrótűvel. /A varrótű végei legyenek letörve, és persze az a jó, ha hossza mentén egyenletes vastagságú/. Ez után egy papírlapon vékony párhuzamos vonalakat húzunk, amelyeknek egymástól való távolsága kétszer olyan nagy, mint a tű hossza. Ezután bizonyos (tetszés szerinti, de állandó) magasságból a tűt a papírra ejtjük és megfigyeljük, hogy metszi-e a tű a vonalak valamelyikét, vagy nem. Hogy a tű ne ugrálhasson, a papírlap alá itatóst vagy posztót teszünk.A tűdobálást sokszor megismételjük, (legalább százszor, ezerszer, vagy esetleg 28 milliószor) és minden alkalommal megnézzük, hogy volt-e metszés. (megj.: Metszésnek számít az az eset is, amikor a tű csak a hegyével érinti a vonalat.) Ha ezután a dobások számát elosztjuk a metszések számával milyen eredményt kapunk?
|
 |
|
|
| [872] jonas | 2005-03-30 18:22:06 |
 Szerintem a 3×3-as felosztásból az is látszik, hogy legfeljebb 9 lyuk maradhat, tehát 11 dominó mellé mindig le lehet rakni még egyet. Egy 3×3-as sarokban ugyanis hat mezőt mindig le kell fedni ahhoz, hogy ne lehessen még egy dominót lerakni. Ez az eredmény megegyezik Gézáéval, és éles is, mert 12 dominó már meg tudja tölteni a táblát.
|
A |
A |
|
B |
|
| C |
C |
|
D |
B |
E |
|
F |
F |
D |
|
E |
| G |
|
H |
I |
I |
|
| G |
J |
H |
|
K |
K |
|
J |
|
L |
L |
|
|
|
| Előzmény: [852] Csimby, 2005-03-29 01:19:33 |
|
| [871] tudniakarok | 2005-03-29 21:56:19 |
 azaz ezért jó a tiéd nem pedig nem jó!na mind1
|
|
| [870] tudniakarok | 2005-03-29 21:49:17 |
 Bár ez meg pl 8-ra nem jó,mert ott 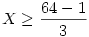 ebből X=21, amit irtál ott meg 22 jön ki (66/3) ebből X=21, amit irtál ott meg 22 jön ki (66/3)
|
|
| [869] tudniakarok | 2005-03-29 21:39:43 |
 Igazad lehet,sőt van!Belebonyolódtam az oszthatóságba!Ez is meg van!
|
|
|
| [867] Csimby | 2005-03-29 21:17:59 |
 k=4-re azt mondja, hogy legalább 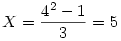 dominót el tudunk helyezni. De szerintem ez az érték 6 kéne, hogy legyen. Vagyis N=6 míg a képlettel N=42-2*5+2=8. Nekem gyanús, hogy k=5-re sem jó, vagyis akkor van baj, amikor k2-1 osztható 3-mal (k=2-re sem jó, míg k=3-ra, és k=6-ra, amikor k2-1 nem osztható 3-mal, olyankor jó). dominót el tudunk helyezni. De szerintem ez az érték 6 kéne, hogy legyen. Vagyis N=6 míg a képlettel N=42-2*5+2=8. Nekem gyanús, hogy k=5-re sem jó, vagyis akkor van baj, amikor k2-1 osztható 3-mal (k=2-re sem jó, míg k=3-ra, és k=6-ra, amikor k2-1 nem osztható 3-mal, olyankor jó).
|
| Előzmény: [866] tudniakarok, 2005-03-29 20:07:52 |
|
| [866] tudniakarok | 2005-03-29 20:07:52 |
 Na akkor kxk-s táblára lerakható még egy dominó,ha N db mező szabad,és X-1 db dominó van lerakva: Kós Géza nyomán: 6X 2(k-1)2+4k-4 ,ebből 2(k-1)2+4k-4 ,ebből
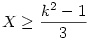
Minden term. szám négyzete vagy osztható 3-mal vagy 1 maradékot ad,ezért
![X=\bigg[\frac{k^2+1}{3}\bigg]](keplet.cgi?k=44CD375480E1B13C) ez a legkevesebb dominó ,ami lerakható a táblára,azaz ez a legkevesebb dominó ,ami lerakható a táblára,azaz
![k^2-2\bigg[\frac{k^2+1}{3}\bigg]](keplet.cgi?k=9308E9F3258B329F) helyünk marad miután az összeset leraktuk,ezért helyünk marad miután az összeset leraktuk,ezért
![N=k^2-2\bigg[\frac{k^2+1}{3}\bigg]+2](keplet.cgi?k=CF3759D7090A57FE)
Nekem eddig minden próbálkozásnál összejött,de azért nem állítom hogy teljesen jó.
|
| Előzmény: [864] levi, 2005-03-29 17:02:04 |
|
| [865] Kós Géza | 2005-03-29 17:29:59 |
 Helyezzünk el k darab dominót úgy, hogy több már ne férjen a táblára. Azt kell megmutatni, hogy k 12. 12.
Számoljuk össze az olyan dominó-rácspont párokat, amikor a rácspont a dominó határán van.
a) Minden dominó határán 6 rácspont van, ez tehát összesen 6k pár.
b) A tábla belsejében levő 25 rácspont mindegyikének legalább két dominóhoz kell illeszkednie, különben még egy dominót odatehetünk mellé. A tábla kerületén levő rácspontokhoz is --- a sarkokat kivéve --- illeszkednie kell legalább egy-egy dominónak. Ilyen rácspontból 20 van. A párok száma tehát legalább 25.2+20.1=70.
Azt kaptuk, hogy 6k 70, vagyis k 70, vagyis k 12. 12.
|
| Előzmény: [863] tudniakarok, 2005-03-29 15:49:34 |
|
| [864] levi | 2005-03-29 17:02:04 |
 Az N számnak mindig párosnak kell lennie, nem? A k szám páros, k*k is páros, és ha elhelyezek egy dominót, akkor mindig 2-vel fog csökkeni, azaz páros lesz mindig a nem üres mezők száma is és a fedett mezők száma is. A sejtés azonban k=8 esetre ez alapján nem jó, mert akkor X=27, ami nem lehetséges.
|
| Előzmény: [859] tudniakarok, 2005-03-29 15:23:03 |
|
| [863] tudniakarok | 2005-03-29 15:49:34 |
 Íme az én bizonyításom a saját feladatomra!: Úgy indulok,ahogy Csimby:Osszuk fel a 6x6-os táblát 4db 3x3-as négyzetre! Mivel 14 mező fedetlen,ezért van olyan résztábla amelyen 4 fedetlen mező van.Megmutatjuk hogy ezen résztáblán van 2 szomszédos mező!Legyen a résztábla a táblázat jobb felső sarka! Tegyük fel hogy az állítással ellentétben nincs 2 szomszédos mező! Ekkor az A B C betűkkel jelölt mezők nem lehetnek fedetlenek,hisz akkor a közbezárt mező is fedetlen volna. Hasonlóan nem lehetnek fedetlenek az x-szel jelölt mezők sem,hiszen akkor C sarokmező is fedetlen volna. Vagyis a bal oldali 2x3-mas táblarészen legalább 4 mező le van fedve,így legfeljebb 2 mező lehet fedetlen! Emiatt az alsó sorban kell lenni 2 fedetlen mezőnek. Feltevésünk szerint nics 2 szomszédos mező,tehát ez a 2 csak a két szélső lehet. Tehát E és F biztosan nincs lefedve. Ebből viszont adódik,hogy a szürke mezőknek fedettnek kell lenni,különben volna 2 szomszédos fedetlen mező. Ugyanakkor az A és C mezők közötti mezőnek is fedettnek kell lenni. Ezt viszont nem lehet megtenni,mert ez a dominó az A B C mezők egyikét lefedné,így nem maradhatna 4 fedetlen mező! Ellentmondásra jutottunk,tehát van két szomszédos fedetlen mező!
|
 |
|
| [862] levi | 2005-03-29 15:45:07 |
 Bocs, már megint nem fogalmaztam pontosan, szóval N az üres mezők száma, de szerencsére valaki rá tudott jönni...
|
|
| [861] tudniakarok | 2005-03-29 15:26:31 |
 ÁÁÁÁÁÁÁ! Ne!!! Igazad van Csimby 14 mező fedetlen vissza az egész,de még ma beírom az én bizonyításom is
|
|
| [860] tudniakarok | 2005-03-29 15:24:25 |
 De ha gondolod beírhatom az én bizonyításom is mert csak a vezérfonal ugyanaz,mint a tiéd,de hát az a lényeg
|
|
| [859] tudniakarok | 2005-03-29 15:23:03 |
 Úgy látom mindenkit félreértek!Bocs! Levit úgy értettem meg,hogy végigböngészetem 16szor amit írt meg az enyémet is itthon,és nekem is kijött úgy ahogy Levinek,úgyhogy egyetértek vele! Na de akkor legyen X az a darabszám amit egy kxk-s táblán lerakva még egyet le tudunk rakni (6x6-osnál X=14) Tehát amit sejtek: 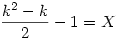 és szerintem legyen k>2 és szerintem legyen k>2
|
|
| [858] Csimby | 2005-03-29 15:16:46 |
 "ugye bizonyítottuk hogy 6x6os táblán 14et elhelyezve még egyet le tudunk rakni,tehát 15öt"
Nem!
Azt bizonyítottuk, hogy ha 11 dominót már leraktunk, akkor biztosan el tudunk helyezni még egyet, vagyis 12-t összesen...
|
| Előzmény: [856] tudniakarok, 2005-03-29 15:04:29 |
|
| [857] Csimby | 2005-03-29 15:13:58 |
 Úgy konkrétan miből értetted meg Levit, ebből: "ha ott is megvizsgálnánk a további sorokat, kijönne az, hogy nem lehet üres mezőt elhelyezni... "? ;-) Egyébként meg szerintem az én bizonyításom (és ezek szerint ilyen a tiéd is) egyáltalán nem hosszú, dehát ízlések és pofonok...
Tényleg nem teljesen világos, de Levinél N nem az elhelyezett dominók száma, hanem az üresen maradt mezők száma úgy, hogy biztosan el tudjunk helyezni még egy dominót (láthatod ezt abból is, hogy k=6-nál N=14, ami a te feladatod). Így stimmel a k=2 és k=4 esetre adott N=2 és N=6.
|
| Előzmény: [855] tudniakarok, 2005-03-29 14:47:26 |
|
| [856] tudniakarok | 2005-03-29 15:04:29 |
 Hopp egy ötlet: azt kell megnézni hogy mennyi helyünk marad a táblán, ha lerakjuk azt az utolsó dominót is, ugye bizonyítottuk hogy 6x6os táblán 14et elhelyezve még egyet le tudunk rakni,tehát 15öt,ez 15x2=30 négyzetet foglal a 36-ból,azaz 6 négyzet üresen marad. 2x2es táblát kizárom,nem érdemes vele foglalkozni! 3x3as táblán N=2-nél még egyet le tudok rakni,azaz 6 négyzetet fedek,3 maradt üresen! 4x4es táblán N=5-nél még egyet lerakva 12 négyzetet fedek,4 maradt üresen!Még nem láttam be,de a sejtés hogy kxk-s táblán k marad üresen,és így: 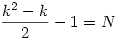
|
|
| [855] tudniakarok | 2005-03-29 14:47:26 |
 Most már értem levit!:) Az én megoldásom szinte ua mint a Csimbié,úgyhogy nem írom be,mert hosszú! Viszont levi azt írja hogy 2x2-es táblán 2-őt elhelyezek és még biztosan el tudok helyezni egyet,lehet hogy én nem értem megint,de ha 2őt elhelyezek,akkor már nincs több hely,mert lefedi az egészet! Ha k=4 akkor szerintem N=5,nem pedig 6.talán
|
| Előzmény: [854] levi, 2005-03-29 13:49:07 |
|
| [854] levi | 2005-03-29 13:49:07 |
 Jonasnak igaza van, a többi sorban nem feltétlenül működik, azonban ha ott is megvizsgálnánk a további sorokat, kijönne az, hogy nem lehet üres mezőt elhelyezni... a közérthetetlenségemért meg elnézést kérek, egyszerűen csak nem tudok fogalmazni... Viszont felmerült bennem egy kérdés: Adott egy k pozitív páros szám. Egy k*k-ás táblázatban elhelyezünk néhány dominót. Melyik az a legkisebb N szám, amelyre igaz, hogy még mindenféleképpen el lehet helyezni még egy dominót, anélkül, hogy a már letett dominókat elmozdítanánk?
k=2-nél szerintem ez 2, k=4-nél talán 6, k=6-nál akkor 14.
|
| Előzmény: [851] tudniakarok, 2005-03-28 23:22:47 |
|
| [853] Csimby | 2005-03-29 01:23:19 |
 A számozásra végül nem lett szükség csak az elején ezt még nem tudtam...
|
|
| [852] Csimby | 2005-03-29 01:19:33 |
 Szerintem bontsuk fel 4 db. 3×3-as négyzetté a 6×6-os négyzetet. Ugye 14 üres mező marad összesen, vagyis lesz olyan 3×3-as négyzet amelyben legfeljebb 5 mezőt fed le dominó (ha mindegyikben legalább 6 mezőt fedne le dominó, akkor 4×6=24, 24+14=38 > 36, ami ellentmondás).
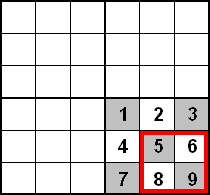
A szimetria miatt mindegy, hogy melyik 3×3-as négyzetben bizonyítjuk, hogy ha csak 5 mezőt fedünk le belőle dominókkal, akkor még egy dominót el tudunk helyezni, tehát legyen ez a jobb alsó 3×3-as négyzet.
Ahhoz, hogy a piros négyzetben ne maradjon hely domionónak, ahhoz mindenképpen el kell helyeznünk 2 teljes dominót a 3×3-as négyzetben. Vagyis biztosan lefedünk 2 szürke és 2 fehér mezőt. Az 5. mező lefedése után tehát vagy 3 szürke és 1 fehér, vagy pedig 2 fehér és 2 szürke mezőnk marad.
Mindegyik fehér mezőnek 3 szürke szomszédja van, tehát bármely fehér mezőhöz csak 2 olyan szürke mező létezik, amely nem mellette található, így ha 3 szürke és 1 fehér mező marad üresen, akkor biztosan lesz hely még egy dominónak.
2 fehér mezőnek vagy 4 vagy 5 szürke szomszédja van, tehát akárhogy is marad üresen 2 szürke és 2 fehér mező, biztosan lesz 2 egymás melletti és így biztosan lesz hely még egy dominónak.
|
 |
| Előzmény: [848] tudniakarok, 2005-03-27 11:42:56 |
|



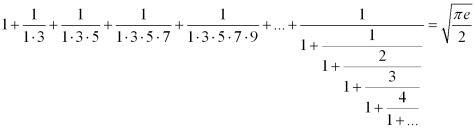

 értékét. Ez akkor világcsúcs volt.
értékét. Ez akkor világcsúcs volt. 


 2(k-1)2+4k-4 ,ebből
2(k-1)2+4k-4 ,ebből 

